Уравнение движения поезда. Методы интегрирования уравнения движения поезда. Методика расчета и построения диаграммы удельных сил, действующих на поезд

52. Уравнение движения поезда.

Уравнение движение поезда – математическое выражение связывающее кинематические параметры движения поезда (скорость, время хода) с величинами действ на него сил

В режиме тяги R=F_к-W_к

В режиме холостого хода

В режиме торможения

Основной задачей уравнения движения поезда является выявление зависимости возможной скорости движения заданного поезда по заданному участку и определение исходя из этой зависимости времени движения поезда по этому участку:

Если в уравнении движения F_к=W_к, или f_к-w_к=0, то на основе этого условия равномерного движения поезда возможно решение следующих задач:

-определение скорости равномерного движения заданного поезда на заданном элементе профиля.

-определение max веса состава поезда для данного локомотива на заданном подъеме с заданной скоростью.

-определение времени хода поезда по участку способом равномерных скоростей.

-анализ характера движения.

53. Методы интегрирования уравнения

движения поезда

Интегрирование уравнения движения поезда позволяет найти зависимость между скоростью, временем движения и пройденным расстоянием.

Известны три метода:

1-аналитический

Точность расчетов выведенными формулами возростает с уменьшением расчетных интервалов.

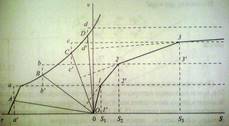
2-графический

Существует несколько способов интегрирования уравнения движения графическим способом. Одним из них является метод Липеца.

3-численный (таблица)

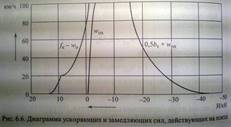
54. Методика расчета и построения диаграммы удельных сил, действующих на поезд.

Анализ характера движения поезда

В виде таблицы производим расчет удельной равнодействующей силы для режимов тяги, холостого хода и торможения используя тяговую характеристику F_т(V) ПТР и рассчитываем общее полное удельное сопротивление движению.

Полученные значения откладываем в виде 3-х графиков в одних координатах V(i) (на одной оси)

55. Тормозные задачи и методика их решения.

Задачи связанные с движением поездов:

-определение тормозных средств, которые могут обеспечить уменьшение скорости или полную остановку поезда на требуемом расстоянии по известным значениям тормозного пути, начальной и конечной скорости торможения.

-определение расстояния, на котором заданный поезд с известными тормозными средствами может остановиться или снизить скорость движения до необходимого значения (определить тормозной путь, начальную и конечную скорость торможения).

Решение тормозных задач можно производить способом аналитического интегрирования уравнения движения:

-при движении х.х.

-при торможении

Полный тормозной путь рассчитывается по формуле:

S_т=S_п+S_д

где  S_т - подготовительный путь

S_п – действительный тормозной путь

S_д – 0,278 V₀·t_п

t_п – зависит от числа осей и вида тормоза; например для грузового состава до 200 осей + автотормоза

где i_с – приведенный уклон;

V_р – расчетный тормозной коэффициент поезда;

φ_кр – расчетный коэффициент трения тормозной колодки.

При аналитическом интегрировании весь диапазон изменения скорости от начальной до конечной разбивают на интервалы при этом:

r_срi – среднее значение удельной равнодействующей силы на

i – ом интервале изменения скорости.

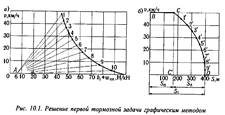
При графическом методе расчета:

1.Строим диаграмму замедляющих сил для торможения

2.Рядом откладываем S_п рассчитанное аналитически

3.Разбиваем диапазон изменения скорости на участки не более 10 км и строим способом Липеца кривую скорости до точки в которой значение скорости = 0