Упруго-пластическое состояние толстостенной трубы, нагруженной внутренним давлением и осевой силой при линейном упрочнении

Упруго-пластическое состояние толстостенной трубы, нагруженной внутренним давлением и осевой силой при линейном упрочнении.

Допустим, что толстостенная труба, внутренний радиус которой r1, а наружный r2, нагружена внутренним давлением р и осевой силой N.

Примем, что материал трубы несжимаем () и имеет линейное упрочнение, т.е. диаграмма деформирования материала может быть схематизирована в виде диаграммы без площадки текучести с линейным упрочнением:

Для бесконечно длинной трубы из условия симметрии очевидно, что поперечные сечения ее при деформации остаются плоскими и перпендикулярными к оси, т.е. осевая деформация трубы не изменяется по радиусу и длине

            (1.1)

для трубы конечных размеров постоянство деформации может быть обеспечено приложением на торцах нормальных сил, распределенных по определенному закону, симметрично относительно оси трубы. Равнодействующая этих сил N определяется величиной осевой деформации. В сечениях, достаточно удаленных от торцов, закон распределения по сечению внутренних нормальных сил не зависит от того, как внешние нормальные силы распределены по торцам. Последнее обстоятельство дает возможность для сечений трубы конечной длины, достаточно удаленных от ее торцов, считать условие (1.1) справедливым.

Допустим, что .                                              (1.2)

В пределах упругости для толстостенной трубы наиболее опасными точками являются точки на внутренней поверхности. В них первоначально возникают пластические деформации и, следовательно, пластическая область примыкает к внутренней поверхности трубы. Из условия симметрии нагружения относительно оси трубы следует, что пластическая область в поперечном сечении трубы представляет собой кольцо. Обозначим радиус границы, разделяющей упругую и пластическую области, через .

Очевидно, что  эта величина характеризует степень распространения пластических деформаций в сечении трубы. Вследствие осевой симметрии нагружения в упруго-пластическом состоянии напряжения, деформации и перемещения являются функциями только радиуса . По этой же причине касательные напряжения в окружном и радиальном сечениях отсутствуют и, следовательно, эти сечения, а также поперечное сечение трубы являются главными. Напряжения в них: радиальное окружное и осевое - главные напряжения.

Радиальное и окружное напряжения в упругой области определяем по формулам:

  (1.3)

Коэффициент  в формулах (1.3) введен перед скобками для удобства последующих выкладок. Он влияет только на величины постоянных интегрирования.

В пределах упругости осевая деформация  связана с осевым , радиальным окружным напряжениями соотношением

.

На основании равенства (1.2) получаем зависимость осевого напряжения от окружного и радиального:

.                (1.4)

для определения напряжений в пластической области используем дифференциальное уравнение равновесия элемента трубы

.   (1.5)

Зависимость компонентов деформаций от компонентов напряжений в решаемой задаче имеют вид:

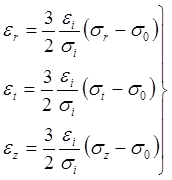                       (1.6)

Зависимость интенсивности напряжений от главных напряжений имеет вид:

  (1.7)

                 (1.8)

Используя условие (1.2), из третьей формулы (1.6) получаем

=

и согласно выражению (1.8)

      (1.9)

Подставляя эту величину в выражение для интенсивности напряжений (1.7), имеем

       (1.10)

Используя выражение (1.10), дифференциальное уравнение равновесия (1.5) приведем к виду

        (1.11)

При отсутствии площадки текучести () для несжимаемого материала ()  при  

,   (1.12)

где - параметр упрочнения.

Подставляя выражение (1.12) в уравнение (1.11), получаем

.     (1.13)

Определим закон изменения интенсивности деформаций.

Используя условие несжимаемости  (в результате пластических деформаций изменения объема не происходит), выражение (1.2) и соотношения, связывающие радиальную  и окружную  деформации с радиальным перемещением  и радиусом :

.   (1.14)

получаем дифференциальное уравнение для радиального перемещения, справедливое как в упругой, так и в пластической областях

.

Интеграл его имеет вид

,       (1.15)

где - постоянная интегрирования.

Согласно формулам (1.14) имеем

.     (1.16)

Из выражения зависимости интенсивности деформаций от главных линейных деформаций

используя соотношения (1.2) и (1.16), получим

.    (1.17)

Подставим выражение (1.17) в уравнение (1.13). Тогда

.

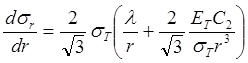В результате интегрирования этого соотношения устанавливаем

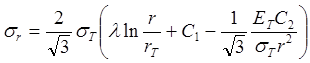,   (1.18)

где - постоянная интегрирования.

Из  соотношений (1.10), (1.12), (1.17), (1.18) и (1.9) имеем

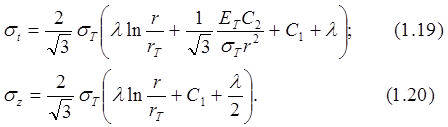
Для определения постоянных используем краевые условия:

1.  при

2.  при

3.  при

4.  при

где индексами  и  отмечены напряжения соответственно в пластической и упругой областях.

Из первого краевого условия, используя выражение (1.18), имеем

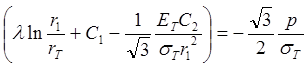.        (1.21)

Из второго краевого условия с помощью формулы (1.3) получаем

.         (1.22)

Третье и четвертое краевые условия с использованием соотношений (1.18), (1.19) и (1.3) дают

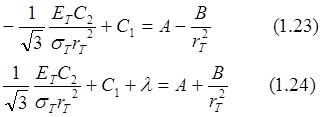
решаем уравнения (1.22)-(1.24) относительно  и , учитывая, что при   и, следовательно, согласно формуле (1.17)

.

Тогда

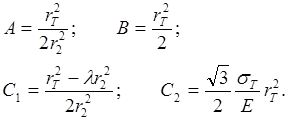           (1.25)

Подставим величины  и  в соотношение (1.21). тогда получим уравнение, связывающее радиус границы, разделяющей упругую и пластическую области, и приложенное давление

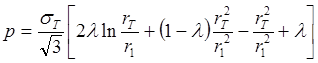.  (1.26)

Это уравнение может быть решено численно или графически.

Подставляя величины постоянных  и ,  по формулам (1.25) в соотношениях (1.18)-(1.20) получим выражения для напряжений в пластической области: