Кривая однородности грунта. Коэффициент пористости, соответствующий влажности на границе текучести. Оценка способности грунта к просадочному явлению

коэффициент сжимаемости грунта для заданного расчетного интервала давлений (). Здесь  и  – коэффициенты пористости, соответствующие давлениям  и ;  – заданный расчетный интервал  давлений (действующее давление), МПа.

 

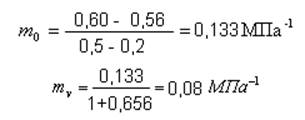Числовые значения коэффициента относительной сжимаемости  позволяют судить о сжимаемости грунтов. При значении 0,08 грунт – среднесжимаемый.

в) Дано:

Построим график сдвига

 

Для определения нормативного значения угла внутреннего трения  следует пользоваться формулами, составленными на основе законов математической статистики:

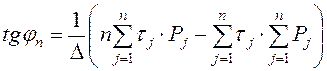, где n – число экспериментов по определению сопротивления грунта сдвигу  при давлении ;  - общий знаменатель этого выражения, определяемый по формуле

.

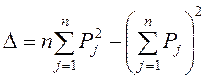Δ = 6 ·0,91 – 4,41 = 0,68

tg φ  = 1/0,68 (6 · 0,3986 – 2,1 · 0,921) = 0,61

φ = arctg φ = 33.93 рад.

Задание 2

К горизонтальной поверхности массива грунта в одном створе приложены три вертикальные сосредоточенные силы: Р₁, Р₂, Р₃, (рисунок 1).  и  – расстояния между осями действия сил. Определить значения вертикальных составляющих напряжений  от совместного действия сосредоточенных сил в точках массива грунта, расположенных в плоскости действия сил:

1) по вертикали I - I, проходящей через точку приложения силы Р₂;

2) по горизонтали II – II, проходящей на расстоянии  от поверхности массива грунта.

Точки по вертикали расположить от поверхности на расстоянии 1,0; 2,0; 4,0; 6,0 м. Точки по горизонтали расположить вправо и влево от оси действия силы Р₂ на расстоянии 0,0; 1,0; 3,0 м. По вычисленным напряжениям и заданным осям построить эпюры распределения напряжений . Исходные данные приведены в таблице 4, схема к расчету – на рисунке 1.

Рисунок  1 - Расчетная схема к заданию 2

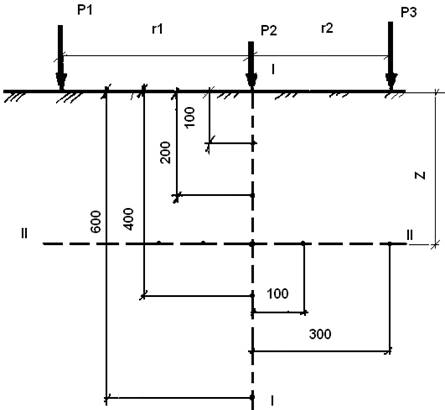
Дано: P₁=1500кН; P₂=1900кН; P₃=700кН; r₁=2м; r₂=2м; z=2,5м.

Для случая, когда к горизонтальной поверхности массива грунта приложено несколько сосредоточенных сил (P1, P2, P3), значения вертикальных составляющих напряжений σ_zi в любой точке массива грунта можно определить суммированием составляющих напряжений от действия каждой силы в отдельности с использованием зависимости

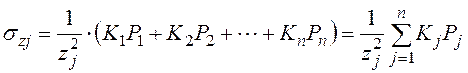, где  – коэффициент, являющийся функцией отношения 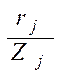. Здесь  –  расстояние по горизонтальной оси от рассматриваемой точки до оси Z, проходящей через точку приложения сосредоточенной силы , м;  – глубина рассматриваемой точки от плоскости приложения сосредоточенной силы , м.

Составим таблицу с данными для всех точек

Точка	Глубина z, м	Расстояние от точки до Pi, ri, м	Коэффициент Ki	Напряжения σzi,кН/м2
		2	0,0085
1	1	0	0,4775	349,85
		3	0,0015
		2	0,0844
2	2	0	0,4775	127,14
		3	0,0251
		2	0,2733
3	4	0	0,4775	65,2
		3	0,1574
		2	0,3664
4	6	0	0,4775	38,98
		3	0,2733
		3	0,0513
5	2,5	1	0,3294	91,34
		2	0,1386
		5	0,0085
6	2,5	3	0,0513	152,95
		0	0,4775
		1	0,3294
7	2,5	1	0,3294	122,03
		4	0,02
		1	0,3294
8	2,5	3	0,0513	16,54
		6	0,0044
		2	0,1386
9	2,5	0	0,4775	102,34
		3	0,0513

Строим эпюры распределения напряжений

 

Задание 3

Горизонтальная поверхность массива грунта по прямоугольным плитам с размерами в плане  и  нагружена равномерно распределенными вертикальными нагрузками интенсивностью Р₁ и Р₂ (рисунок 2). Определить вертикальные составляющие напряжений  от совместного действия внешних нагрузок в точках массива грунта для заданной вертикали, проходящей через одну из точек М₁, М₂, М₃. Расстояние между осями плит нагружения . Точки по вертикали расположить от поверхности на расстоянии 1,0; 2,0; 4,0 и 6,0 м. По вычисленным напряжениям построить эпюру распределения напряжений .

V

IV

III

II

I

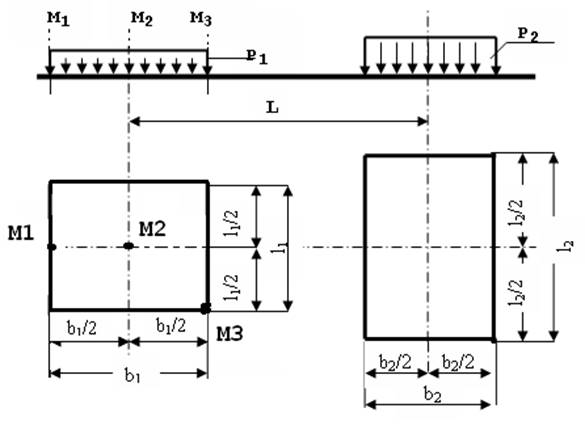
Рисунок 2 – Расчетная схема к заданию 3

Дано: l₁=2,7м; b₁=1,9м; l₂=3,5м; b₂=2,5м; P₁=320кПа; P₂=340кПа; L=3,4м; точка M3.

Распределение по глубине вертикальных составляющих напряжений  в любой точке массива грунта от действия равномерно распределенной нагрузки в пределах или за пределами плит нагружения может быть определено  по методу угловых точек по формуле

, где α – коэффициент, определяемый в зависимости от отношения сторон прямоугольной площади загружения (путем интерполяции)  ( – большая сторона,  – меньшая сторона) и отношения (z – глубина, на которой определяется напряжение );  – интенсивность равномерно распределенной нагрузки, кН.

Номер прямоугольной плиты и участков	Равномерно распределенная нагрузка Pi,кПа		Величина заглубления zi, м		α	σziM3
I	320	1,4	1	0,53	0,3109	24,87
			2	1,05	0,1935	15,48
			4	2,11	0,0772	6,18
			6	3,16	0,0406	3,25
II	340	2,1	1	0,57	0,3565	30,3
			2	1,14	0,1966	16,71
			4	2,31	0,0869	7,387
			6	3,43	0,0505	4,293
III	340	2.1	1	0,57	0,3565	30,3
			2	1,14	0,1966	16,71
			4	2,31	0,0869	7,387
			6	3,43	0,0505	4,293
IV	340	1.5	1	0,83	0,2351	19,98
			2	1,67	0,1134	9,64
			4	3,33	0,0406	3,45
			6	5	0,0179	1,52
V	340	1.5	1	0,83	0,2351	19,98
			2	1,67	0,1134	9,64
			4	3,33	0,0406	3,45
			6	5	0,0179	1,52

Для начала определим  напряжения от нагрузки P₁(I) на заглублениях

σ^Р1_z1M3 = 24.87

σ^Р1_z1M3 = 15.48

σ^Р1_z1M3 = 6.18

σ^Р1_z1M3 = 3.25

далее сумму напряжений от нагрузки P₂ (II, III) на заглублениях

σ^Р2_z1M3 = 60,6

σ^Р2_z1M3 = 33,42

σ^Р2_z1M3 = 14,774

σ^Р2_z1M3 = 8,586

сумму напряжений соответствующую IV и V от нагрузки P₂ на заглублениях

σ^-Р2_z1M3 = 39,96

σ^-Р2_z1M3 = 19,28

σ^-Р2_z1M3 = 6,9

σ^-Р2_z1M3 = 3,04

Вертикальные составляющие напряжений σ_z от совместного действия внешних нагрузок в точке М3

σ_z1M3 = 45,51

σ_z1M3 = 29,62

σ_z1M3 = 14,054

σ_z1M3 = 8,796

Строим эпюру распределения напряжений

 

Задание 4

Откосы котлована глубиной  проектируются с заложением . Грунт в состоянии природной влажности имеет следующие характеристики физико–механических свойств: удельный вес грунта , угол внутреннего трения , удельное сцепление . Определить методом круглоцилиндрических поверхностей скольжения коэффициент устойчивости откоса. Исходные данные приведены в таблице 6, схема к расчету представлена на рисунке 3.

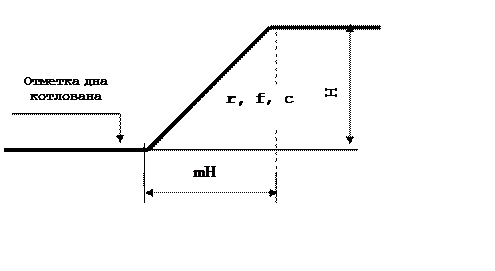
Рисунок 3 - Расчетная схема к заданию 4

Дано: H=13м; m=2,0; γ=19,7кН/м²; φ=20°; C=19кПа.

Для начала определим координаты центра вращения

где γ – удельный вес грунта; H – глубина; φ – угол внутреннего трения; C – удельное сцепление.

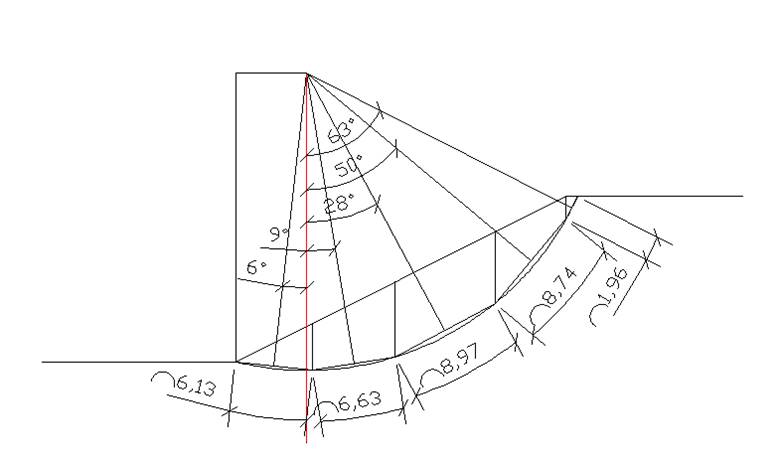
5

tg α = H\ mH = 1/m = 0.5

arctg 0.5 = 26.57, => α = 27º

Координаты центра вращения: x₀ = 0.43, у₀ = 1,75.

Тогда координаты центра вращения 0 составят

Х = х₀ · Н = 0,43 · 13 = 5,59 м,

У = у₀ · Н = 1,75 · 13 = 22,75 м.

Объем участков:

V₁ = S₁ · 1 м = 11.12 м

V₂ = S₂ · 1 м = 31.24 м

V₃ = S₃ · 1 м = 45.12 м

V₄ = S₄ · 1 м = 20.41 м

V₅ = S₅ · 1 м = 0.78 м

G₁ = V₁· γ = 11.21 · 19.7 = 219.06

G₂ = V₂· γ = 31.24 · 19.7 = 615.43

G₃ = V₃· γ = 45.12 · 19.7 = 888.86

G₄ = V₄· γ = 20.41 · 19.7 = 402.08

G₅ = V₅ · γ = 0.78 · 19.7 = 15.37

Найдем силу трения:

N₁ = G₁ · cos Θ₁ = 219.06 · cos 6 º = 217.9

N₂ = G₂ · cos Θ₂ = 615.43 · cos 9 º = 607.85

N₃ = G₃ · cos Θ₃ = 888.86 · cos 28 º = 784.82

N₄ = G₄ · cos Θ₄ = 402.08 · cos 50 º = 258.45

N₅ = G₅ · cos Θ₅ = 15.37 · cos 63 º = 6.98

Найдем касательную составляющую, способствующую скольжению отсека: