Понятие о форме и размерах земли. Системы географических и геодезических координат. Зональная система прямоугольных координат Гаусса

Камеральные работы по обработке  результатов измерений,  проведенных при прокладке теодолитных ходов, начинают с проверки  и обработки  полевых журналов: повторно выполняют асе вычисления  и выводят среднее значение измеренных горизонтальных (до 0,΄1) и вертикальных (до 1,΄0 )углов и длин сторон (до 0,01 м).  Полученные окончательные средние  значения выделяют – обводят чернилами или подчеркивают. Проверявший журнал делает в нем  соответствующую запись и подписывается.

Затем на плотной бумаге по полученным средним значениям  углов и длинам сторон при  помощи   транспортира и линейки  составляют в произвольном масштабе схему теодолитных ходов. На схеме показывают все включенные в ход твердые пункты  с их  координатами и дирекционными углами  исходных сторон, средние значения горизонтальных углов, длины сторон и углы их наклона  к горизонту, а также ориентирование схемы относительно направления меридиана.

Вычисление координат точек теодолитного хода  производят  в специальной ведомости.

Уравнивание углов. Уравнивание углов замкнутого теодолитного  хода. Суммируют n измеренных внутренних углов полигона (рисунок 41, а), кроме примычного угла β΄_В. Теоретическая сумма внутренних углов плоского многоугольника составит

 , где n – число вершин многоугольника.

Разность f_β между суммой измеренных углов и  теоретической суммой углов называется угловой невязкой хода  (полигона), т.е.

Если бы результаты измерений не имели погрешностей, то угловая невязка f_β равнялась  бы нулю. Отсюда следует, что  величина угловой невязки характеризует качество измерения углов.

Предельно допустимую погрешность угловых измерений  вычисляют по формуле

, где n – число углов в ходе.

Если выполняется условие

, то точность  полевых измерений углов считается  удовлетворительной. В противном  случае в результатах измерений или  в вычислениях имеется недопустимая погрешность, которую нужно  обнаружить и устранить.

При упрощенном уравнивании  полученную угловую невязку  распределяют с обратным знаком поровну во все измеренные углы.  Поправка в каждый  угол будет

Если невязка f_β  не делится без остатка на число углов n,  то  несколько большие по абсолютной величине поправки вводят в углы  с короткими сторонами. Поправки  записывают над  соответствующими углами. Тогда исправленный угол будет

.

Контролем  правильности вычисления поправок является  выполнение условия

, а правильности их введения в углы – условие

,

Уравнение углов разомкнутого теодолитного хода. В  этом случае (рисунок 41, б) вначале вычисляют по формуле  дирекционные углы всех сторон хода:

. . . . . .. . . .  . ..

Сложив  эти равенства, будем иметь

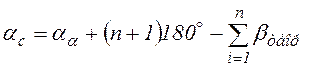, откуда

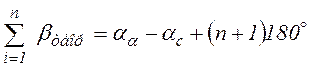
Подставляя полученное  значение  в формулу получим угловую невязку разомкнутого хода

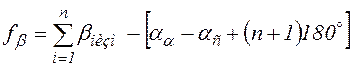
Если измерены левые углы хода, то формулы  соответственно будут иметь вид

,

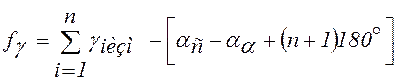
Уравнивание  разомкнутых теодолитных ходов производят так  же, как и замкнутых.

Вычисление дирекционных углов, румбов и горизонтальных  проложений сторон теодолитного хода. Вычисление дирекционных углов. Дирекционные углы сторон теодолитного хода вычисляют  по формулам для правых углов или – для левых  углов.  Контролем правильности вычисления дирекционных углов  сторон замкнутого хода является вторичное получение  дирекционного угла первой станции.  Для разомкнутого хода – получение  конечного дирекционного угла.

Вычисление румбов. Румбы сторон теодолитного хода  вычисляют по соотношениям.  Правильность  получения румбов сторон хода можно  контролировать  вычислением по ним горизонтальных углов между смежными сторонами  хода.

Вычисление горизонтальных проложений сторон теодолитного  хода.  Поправка за наклон сторон хода к горизонту учитывается,  если угол наклона ее больше  1˚,5. Для этого пользуются формулами или специальными таблицами поправок