




1. Проектирование основного механизма.
1.1 Проектирование кривошипно-коромыслового механизма.
Проектирование ведется по коэффициенту изменения средней скорости выходного звена Kω. Координаты звена CD в крайних положениях определяем из геометрических соображений по рисунку 2.
Исходные данные:
1) длина звена CD, l3 = lCD = 0.3 м;
2) координаты звена CD в крайних положениях:
γ2 = 82.5°; γ1 = 127.5°;
3) коэффициент изменения средней скорости поршня при прямом и обратном ходах Kω = ωобр/ωпр = 1.12.
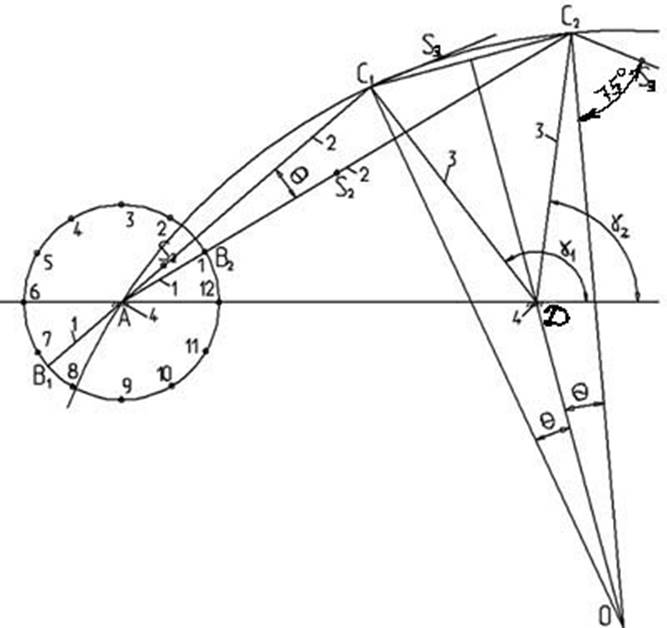
Рисунок 2
Масштаб рисунка 2 μl = 217 мм/м.
Определяем угол q из известного соотношения:
q = 180*(Kω –1)/( Kω+1) = 180*(1.12-1)/(1.12+1) = 10.2°;
Строим равнобедренный треугольник OC1C2, в котором угол Ð С1OC2=2q. Окружность с радиусом r = lOC1 является геометрическим местом центра вращения кривошипа, поскольку в любой точке этой окружности вписанный угол Ð С1AC2 равен половине центрального угла: Ð С1OC2=2q. Следовательно, Ð С1AC2=q.
Далее принимаем обозначения:
l1 – длина кривошипа;
l2 – длина шатуна;
l4 – расстояние между точками A и D.
Измеряются полученные отрезки:
lAC2 = 130 мм; lAC1 = 84 мм; l4 = 102 мм;
Составим систему из 2 уравнений:
l1 + l2 = lAC2,
l2 – l1 = lAC1;
Решая эту систему, получим: l2 = 107 мм; l1 = 23 мм;
Или с учетом масштаба окончательно получим:
l1 = lAB = 0.11 м; l2 = lBC = 0.49 м; l4 = lAD = 0.47 м.
1.2Силы, действующие на звенья механизма.
На звенья механизма действуют следующие силы и моменты:
1) движущие силы FД или моменты МД, развиваемые двигателем. Сила считается движущей, если её работа за один период цикла положительна (даже в том случае, когда она знакопеременна);
2) силы FC или моменты МС полезного сопротивления – силы (моменты), возникновение которых предопределяется технологическим процессом рабочей машины. Работа этих сил (моментов) за один период цикла отрицательна;
3) силы тяжести Gi отдельных звеньев механизма.
1.3Нахождение значений передаточных функций.
Для нахождения передаточных отношений и передаточных функций угловая скорость не важна, т.к. кинематические передаточные функции не зависят от уравнения движения механизма (строится план возможных скоростей). С помощью программы "Диада" были получены значения необходимых передаточных функций, результаты приведены в таблице 2.
Таблица 2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
Vqc, м |
0 |
0.074 |
0.107 |
0.111 |
0.092 |
0.057 |
0.014 |
0.031 |
0.076 |
0.12 |
0.138 |
0.092 |
|
Vqs2, м |
0.071 |
0.097 |
0.107 |
0.108 |
0.099 |
0.088 |
0.073 |
0.073 |
0.097 |
0.11 |
0.106 |
0.077 |
|
U21 |
-0.22 |
-0.11 |
-0.01 |
0.06 |
0.13 |
0.19 |
0.22 |
0.21 |
0.12 |
-0.05 |
-0.23 |
-0.31 |
|
U31 |
0 |
0.25 |
0.36 |
0.37 |
0.31 |
0.19 |
0.05 |
-0.1 |
-0.25 |
-0.4 |
-0.46 |
-0.31 |
Выбираем масштаб построения графиков передаточных функций и передаточных отношений:
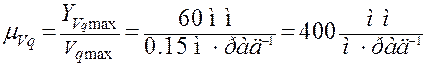
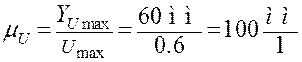
![]()
Строим графики Vq и U.
1.4 Построение графиков приведенных моментов.
Чтобы упростить определение закона движение механизма, заменяем
реальный механизм одномассовой динамической моделью и находим приложенный к ее
звену суммарный приведенный момент сопротивления ![]() .
.
Приведенный момент ![]() , заменяющий силу
сопротивления
, заменяющий силу
сопротивления ![]() и моменты трения в шарнирах A, C и D,
определим в каждом положении механизма по формуле:
и моменты трения в шарнирах A, C и D,
определим в каждом положении механизма по формуле:
![]() , где
, где ![]() - линейная спорость точки С
приложения силы;
- линейная спорость точки С
приложения силы; ![]() -
угловая скорость звена динамической модели, равная угловой скорости начального
звена механизма; U21 и U31
– соответствующие передаточные функции.
-
угловая скорость звена динамической модели, равная угловой скорости начального
звена механизма; U21 и U31
– соответствующие передаточные функции.
Из условия известно, что
Fc = p*A*cos(Fc;Vc), где p = αkp0 – ветровая нагрузка на рефлектор; α=0.5, k=1.5, p0=500 Па; A = πD2/4 – площадь рефлектора;
Также нам понадобятся следующие исходные данные:
D=1 м; ![]() =9.5 H*м;
=9.5 H*м;
![]() =12.3 H*м;
=12.3 H*м; ![]() =14.2
H*м; m2=1.5 кг; m3=45 кг.
=14.2
H*м; m2=1.5 кг; m3=45 кг.
Следовательно, Fc = 0.5*1.5*500*π*12*cos(Fc;Vc)/4 = 294.5*cos(Fc;Vc) Н
Для расчета приведенного момента от сил тяжести используем аналогичную формулу:
![]()
Сведем другие известные нам величины в таблицу 3:
Таблица 3
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
Ð(Fc;Vc), градус |
0 |
1.6 |
11 |
22.1 |
32.3 |
39.9 |
43.5 |
137 |
143 |
153 |
166 |
177 |
|
Ð(G2;VS2), градус |
150 |
115 |
88 |
60 |
40 |
10 |
25 |
65 |
100 |
118 |
130 |
150 |
|
Ð(G3;VS3), градус |
0 |
110 |
105 |
89 |
85 |
78 |
75 |
105 |
100 |
93 |
72 |
70 |
Далее, подставляя исходные данные в соответствующие формулы, получим:
Таблица 4
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
-11.76 |
6.86 |
16.22 |
15.51 |
6.47 |
-2.86 |
-11 |
-18.78 |
-31 |
-46.4 |
-58.3 |
-44.2 |
|
|
-0.92 |
-12 |
-12.52 |
-0.06 |
4.74 |
6.63 |
2.62 |
-3.15 |
-5.7 |
-3.6 |
18.2 |
13.2 |
|
|
-12.68 |
-5.14 |
-3.7 |
15.45 |
11.21 |
3.77 |
-8.38 |
-21.92 |
-36.7 |
-50 |
-40.1 |
-31 |
Выбираем масштаб по оси ординат графика ![]() :
:
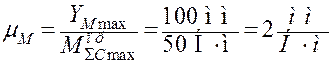 .
.
Масштаб по оси абсцисс ![]() .
.
Здесь 240 мм – выбранная база графика, угол поворота ![]() звена 1 за цикл равен
звена 1 за цикл равен ![]() рад.
рад.
Строим график ![]() .
.
1.5 Построение графика суммарной работы![]() .
.
Суммарная работа сопротивления ![]() всех сил равна работе
всех сил равна работе![]() :
:
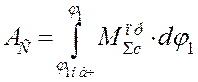 .
.
График ![]() строим методом
графического интегрирования графика
строим методом
графического интегрирования графика ![]() , выбрав отрезок
интегрирования K=80 мм. Масштаб графика
, выбрав отрезок
интегрирования K=80 мм. Масштаб графика ![]() по
оси ординат
по
оси ординат
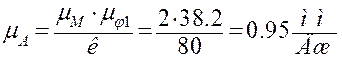 ,
,
![]() .
.
После того как построили
график ![]() ,
откладываем ординату при
,
откладываем ординату при ![]() в
“плюс” и проводим из начала ординат прямую – линию
в
“плюс” и проводим из начала ординат прямую – линию![]() .Тогда сумма:
.Тогда сумма: ![]() +
+![]() даст нам
даст нам ![]() .
.
А, зная ![]() , можем получить
, можем получить ![]() : под углом (равным углу
наклона прямой
: под углом (равным углу
наклона прямой ![]() к абсциссе
к абсциссе
![]() ) из конца
отрезка интегрирования проводим прямую до пересечения с осью
) из конца
отрезка интегрирования проводим прямую до пересечения с осью ![]() на
графике моментов (операция по типу обратного интегрирования).
на
графике моментов (операция по типу обратного интегрирования).
Из графика получаем, что ![]() .
.
1.6 Построение
графиков приведенных моментов инерции ![]()
II группы звеньев.
Графики переменных
приведенных моментов инерции ![]() звеньев II группы строим по формулам:
звеньев II группы строим по формулам:
![]() ;
; ![]() ;
; ![]() ,
,
Кроме того, нам известно, что m2 = 1.5 кг, m3= 45 кг.
Построим зависимости ![]() и
их сумму
и
их сумму ![]() ,
,
Выбираем масштабы по осям:
![]() ;
; ![]() .
.
Результаты вычислений приведены в таблице 5:
Таблица 5
|
|
|
|
|
|
1 |
0.0062 |
0.0001 |
0.0063 |
|
2 |
0.0097 |
0.08 |
0.0897 |
|
3 |
0.0171 |
0.166 |
0.183 |
|
4 |
0.019 |
0.175 |
0.194 |
|
5 |
0.0149 |
0.123 |
0.138 |
|
6 |
0.0095 |
0.046 |
0.056 |
|
Окончание таблицы 5 |
|||
|
7 |
0.0065 |
0.0032 |
0.0097 |
|
8 |
0.007 |
0.0128 |
0.02 |
|
9 |
0.0105 |
0.08 |
0.091 |
|
10 |
0.025 |
0.205 |
0.23 |
|
11 |
0.0352 |
0.271 |
0.31 |
|
12 |
0.0253 |
0.123 |
0.1483 |
1.7 Построение графика
кинетической энергии ![]()
II группы звеньев.
График кинетической энергии ![]() (приближенный) II
группы звеньев получим, выполнив переход от построенного графика
(приближенный) II
группы звеньев получим, выполнив переход от построенного графика ![]() , пересчитав масштаб по формуле
, пересчитав масштаб по формуле
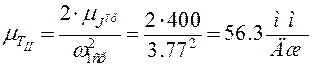 , где
, где ![]() - средняя
угловая скорость вращения кривошипа.
- средняя
угловая скорость вращения кривошипа.
1.8 Построение
графика кинетической энергии ![]()
I группы звеньев.
График кинетической энергии ![]() I группы
звеньев (приближенный) строим по уравнению:
I группы
звеньев (приближенный) строим по уравнению:
![]() ,
,
![]() ,
, ![]() .
.
Необходимые данные и результаты запишем в таблицу 6.
Таблица 6
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
0 |
3.17 |
10.64 |
23.27 |
38 |
49.8 |
56.32 |
55.9 |
47.9 |
32.1 |
16 |
4.53 |
|
|
0.047 |
0.62 |
1.28 |
1.4 |
1.21 |
0.38 |
0.07 |
0.14 |
0.66 |
1.61 |
2.2 |
1.07 |
|
|
-0.047 |
2.55 |
9.36 |
21.87 |
36.79 |
49.42 |
56.25 |
55.76 |
47.24 |
30.49 |
13.8 |
4.46 |
1.9 Определение необходимого момента инерции
маховых масс ![]() .
.
Определяем необходимый момент инерции маховых масс ![]() .
.
Максимальное изменение ![]() за
период цикла:
за
период цикла:
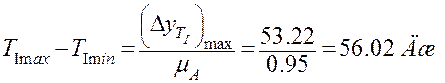
Тогда, т.к. δ=1/42 < 1/20, то можно воспользоваться формулой:
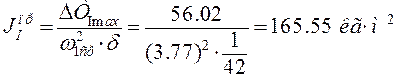
1.10 Построение графика (приближенного) угловой
скорости![]() .
.
График (приближенный) угловой скорости ![]() получаем, совершая переход от
графика
получаем, совершая переход от
графика ![]() , т.е. определяем масштаб угловой
скорости по формуле:
, т.е. определяем масштаб угловой
скорости по формуле:
![]()
Линию ![]() определяем,
как прямую, проходящую через середину отрезка
определяем,
как прямую, проходящую через середину отрезка
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.