


















Пока было общепризнанным, что погрешности на основании центральной предельной теоремы всегда должны быть распределены нормально, задача определения формы распределения погрешностей, естественно, не ставилась. Однако сомнение во всеобщности нормального распределения существовало давно. Так, еще М.Ф. Маликов приводил слова физика Липпмана: «Все верят в закон погрешностей, ибо экспериментаторы думают, что этот закон — математическая теорема, а математики считают, что он установлен экспериментальным путем».
Тем не менее, заблуждение о правомерности лишь нормального распределения погрешностей продолжает существовать до сих пор.
Обоснованное решение многих задач требует идентификации формы распределения погрешностей.
Идентификация распределений нужна и потому, что рассеяние многих оценок зависит от формы закона распределения. Для обеспечения одной и той же погрешности в определении оценки при одном законе можно ограничиться достаточно малой выборкой, тогда как при другом — выборка исходных данных должна быть значительно больше. Совершенно необходимо знание вида закона распределения при определении одних параметров закона распределения по другим его параметрам. Так, например, квантили, т. е. значения погрешности с заданной доверительной вероятностью, без знания вида закона распределения не могут быть выражены через среднее квадратическое отклонение. И, наконец, изменение вида закона распределения погрешностей нередко может служить признаком какого-либо резкого изменения условий проведения измерений. Например, объединение нескольких серий наблюдений, в одной из которых возникла заметная систематическая погрешность, приводит к образованию двухмодального распределения, в то время как в обычных условиях оно было одномодальное.
Экспериментальные данные о разнообразии форм распределения погрешностей измерений накоплены в достаточном количестве. Так, например, проводились исследования законов распределения погрешностей электромеханических приборов на кернах, электронных приборовх для измерения температур и усилий, цифровых приборов с ручным уравновешиванием. Объем выборок экспериментальных данных для каждого экземпляра составлял 100-400 отсчетов. Только у одного из 47 распределений погрешностей оценки оказались близкими к нормальному закону распределения. Все же остальные распределения отличались от нормального.
В итоге этих работ факт разнообразия законов распределения погрешностей был признан законодательно — с 1 января 1974 г. был введен в действие ГОСТ 8.011—72, устанавливающий, что при сообщении размера погрешности результата измерения целесообразно указывать вид распределения, и были стандартизованы модели равномерного, трапецеидального, треугольного, нормального и двухмодальных распределений.
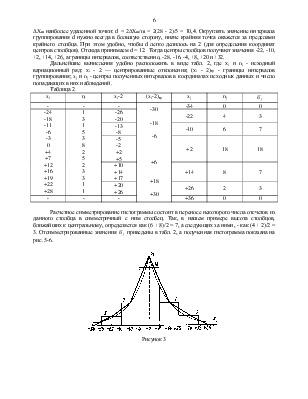
Возможность идентификации формы распределения экспериментальных данных ограничена, прежде всего, малостью объема выборки. При большом объеме выборки, например в несколько тысяч наблюдений, построение гистограммы часто позволяет получить достаточно плавную кривую, отражающую все характерные особенности наблюдаемого закона. При малом объеме выборки (n = 20-200) особенности распределения оказываются замаскированными случайностью самой выборки. Таким образом, малость выборки укрупняет возможные классы идентификации и сокращает их число, а следовательно, более тонкая идентификация формы распределения возможна лишь при соответствующем увеличении объема выборки экспериментальных данных.
Следовательно, приобретает большое значение накопление данных и составление каталога распределений погрешностей различных средств измерений (датчиков, приборов), различных широко применяемых методов измерений, с тем, чтобы этими данными можно было затем пользоваться и при наличии малых серий измерений.
Для определения оценок математического ожидания, с. к. о., эксцесса или контрэксцесса не требуется какого-либо группирования экспериментальных данных. Эти оценки могут быть найдены непосредственно по исходной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.