


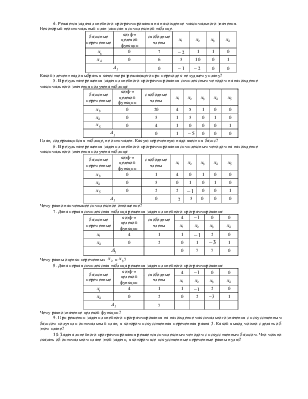

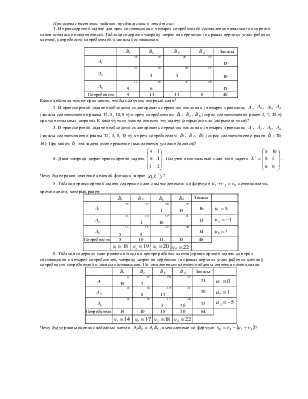




надо сделать, чтобы привести задачу линейного программирования
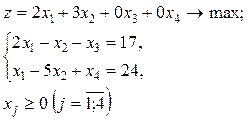
к предпочтительному виду?
Студент должен знать алгоритм решения задач линейного программирования графическим методом, все понятия, встречающиеся в графическом методе, и уметь применять этот алгоритм при решении задач линейного
программирования.
Примерные тестовые задания, предлагаемые в этой теме:
1. В какой из
точек построенной области допустимых решений функция ![]() достигает максимального и минимального
значения?
достигает максимального и минимального
значения?
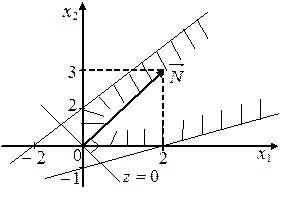
2. В какой из
точек области ![]() допустимых
решений функция
допустимых
решений функция ![]() достигает максимального
достигает максимального
и минимального значения?
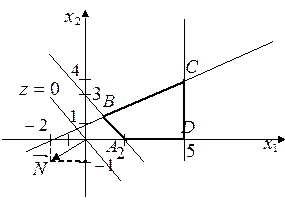
3. Построить
область допустимых решений неравенства ![]() .
.
4. Каковы
координаты градиента функции (вектора ![]() )
в следующей задаче линейного программирования:
)
в следующей задаче линейного программирования:
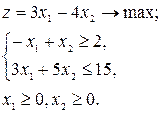
5. При решении задачи линейного программирования получили область допустимых решений.
Найти максимальное значение
функции ![]() .
.
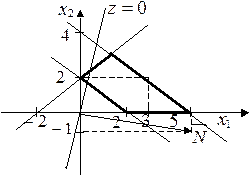
6. Построить
линию нулевого уровня ![]() , соответствующую
целевой функции
, соответствующую
целевой функции ![]() .
.
7. Построить область допустимых решений задачи линейного программирования:
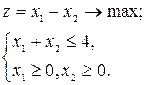
Студент должен знать алгоритм решения задач линейного программирования симплексным методом, знать признак бесконечности множества оптимальных планов, признак неограниченности целевой функции, алгоритм решения задач линейного программирования симплексным методом с искусственным базисом. Студент должен уметь применять алгоритм решения задач линейного программирования симплексным методом на практических примерах.
Примерные тестовые задания, предлагаемые в этой теме:
1. Что можно сказать о плане, содержащемся в таблице?
|
базисные переменные |
коэф-т целевой функции |
свободные члены |
|
|
|
|
|
|
|
0 |
20 |
4 |
5 |
1 |
0 |
0 |
|
|
0 |
3 |
1 |
3 |
0 |
1 |
0 |
|
|
0 |
4 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
|
0 |
0 |
0 |
||
2. В результате решения задачи линейного программирования симплексным методом на нахождение максимального значения получена таблица:
|
базисные переменные |
коэф-т целевой функции |
свободные члены |
|
|
|
|
|
|
|
0 |
20 |
4 |
5 |
1 |
0 |
0 |
|
|
0 |
3 |
1 |
3 |
0 |
1 |
0 |
|
|
0 |
4 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
|
0 |
0 |
0 |
||
Выпишите содержащийся в ней план.
3. Пусть в задаче линейного программирования требуется найти максимальное значение целевой функции.
В каком случае будет получен оптимальный опорный план?
4. Решается задача линейного программирования на нахождение максимального значения.
Некоторый неоптимальный план записан в симплексной таблице.
|
базисные переменные |
коэф-т целевой функции |
свободные члены |
|
|
|
|
|
|
0 |
7 |
|
1 |
1 |
0 |
|
|
0 |
6 |
3 |
10 |
0 |
1 |
|
|
0 |
|
|
0 |
0 |
|
Какой элемент надо выбрать в качестве разрешающего при переходе к нехудшему плану?
5. В результате решения задачи линейного программирования симплексным методом на нахождение максимального значения получена таблица:
|
базисные переменные |
коэф-т целевой функции |
свободные члены |
|
|
|
|
|
|
|
0 |
20 |
4 |
5 |
1 |
0 |
0 |
|
|
0 |
3 |
1 |
3 |
0 |
1 |
0 |
|
|
0 |
4 |
1 |
0 |
0 |
0 |
1 |
|
|
0 |
1 |
|
0 |
0 |
0 |
|
План, содержащийся в таблице, не оптимален. Какую переменную надо ввести в базис?
6. В результате решения задачи линейного программирования симплексным методом на нахождение максимального значения получена таблица:
|
базисные переменные |
коэф-т целевой функции |
свободные члены |
|
|
|
|
|
|
|
0 |
1 |
4 |
0 |
1 |
0 |
0 |
|
|
0 |
3 |
0 |
1 |
0 |
1 |
0 |
|
|
0 |
2 |
2 |
|
0 |
0 |
1 |
|
|
0 |
|
3 |
|
0 |
0 |
|
Чему равно наименьшее симплексное отношение?
7. Дана первая симплексная таблица решения задачи линейного программирования:
|
базисные переменные |
коэф-т целевой функции |
свободные члены |
4 |
|
0 |
0 |
|
|
|
|
|
|||
|
|
4 |
1 |
1 |
|
2 |
0 |
|
|
0 |
2 |
0 |
1 |
|
1 |
|
|
0 |
? |
? |
0 |
||
Чему равны оценки переменных ![]() и
и
![]() ?
?
8. Дана первая симплексная таблица решения задачи линейного программирования:
|
базисные переменные |
коэф-т целевой функции |
свободные члены |
4 |
|
0 |
0 |
|
|
|
|
|
|||
|
|
4 |
1 |
1 |
|
2 |
0 |
|
|
0 |
2 |
0 |
2 |
|
1 |
|
|
? |
|||||
Чему равно значение целевой функции?
9. При решении задачи линейного программирования на нахождение максимального значения с искусственным базисом получили оптимальный план, в котором искусственная переменная равна 3. Какой вывод можно сделать об этом плане?
10. Задача линейного программирования решается симплексным методом с искусственным базисом. Что можно сказать об оптимальном плане этой задачи, в котором все искусственные переменные равны нулю?
Студент должен знать правила построения двойственной задачи и уметь применять их на практических примерах.
Примерные тестовые задания, предлагаемые в этой теме:
1. Дана исходная задача линейного программирования:
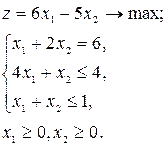
Построить двойственную задачу.
2. Пусть в исходной задаче находится минимум целевой функции. Для составления двойственной ей задачи основные ограничения должны иметь знак …
3. Пусть в исходной задаче находится максимум целевой функции. Для составления двойственной ей задачи основные ограничения должны иметь знак …
4. Дана задача линейного программирования:
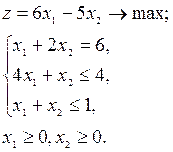
Чему равно количество двойственных переменных?
5. Пусть исходная задача линейного программирования имеет оптимальное решение, что можно сказать о решении двойственной к ней задачи?
6. Пусть целевая функция исходной задачи линейного программирования
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.