6. Измерение входного и выходного сопротивления каскада
Для
измерения входного сопротивления использовался измерительный резистор,
подключаемый ко входу каскада. По измеренным напряжениям на выводах резистора
можно определить ток входа, напряжение входа и отсюда сопротивление каскада.
Вычисление сопротивления проводится по формуле: ![]() .
Процесс итерационный и постепенно сходится.
.
Процесс итерационный и постепенно сходится.
По данным итераций можно сделать вывод, что входное сопротивление каскада равно примерно 638 Ом.
Аналогичным образом было измерено выходное сопротивление каскада. Для этого вход был заземлен, а источник сигнала подключен через измерительное сопротивление к выходу схемы. Сопротивление нагрузки было удалено, Измерительное менялось, руководствуясь теми же правилами, что и при измерении выходного сопротивления каскада.
Таким образом, наиболее близкие значения получились при измерительном сопротивлении равном 3300 Ом, в таком случае выходное сопротивление каскада оказывается равным 3465 Ом, что меньше расчетного значения.
7. Выводы
В данной работе мы исследовали простейший усилительный каскад на одном транзисторе. В очередной раз мы сталкиваемся с большим разбросом значений характеристик полупроводникового элемента, что делает невозможным точно рассчитать все параметры до получения экспериментальных данных. Тем не менее, даже если мы узнаем все характеристики точно, они будут достаточно сильно изменяться с ростом температуры.
Амплитудная характеристика каскада в достаточной степени линейна и согласуется с теоретическими расчетами. Приведенные теоретические расчеты сделаны с учетом точного значения h21, который был измерен в ходе работы. Для низких уровней входных сигналов теория и практика очень близки. Для более высоких напряжений сигнала экспериментальная зависимость лежит ниже практической. В зависимости присутствуют точки, в которых входной сигнал несколько превышает критический уровень, после которого начинаются искажения. С ростом входного напряжения различие теории и практики увеличивается. Это объясняется как раз этими самыми искажениями, которые носят характер отсечения части синусоиды. Определить точно границу появления этого среза достаточно сложно. Это объясняется погрешностью осциллографа и тем, что в верхней точке, производная кривой равна нулю. Отличить верх синуса от кусочка прямой с учетом этой самой погрешности проблематично. Таким образом более раннее расхождение зависимостей может быть объяснено неточностью определения максимального входного сигнала, не вызывающего искажений выходного. После начала отсечки мы должны наблюдать прекращение увеличения уровня сигнала, поскольку его амплитуда не увеличивается. На практике это не так, потому что, вольтметр является интегрирующим элементом, а с ростом входного напряжения на выходе мы хоть и не имеем увеличения амплитуды, но площадь под выходной диаграммой увеличивается. Это и есть причина более медленного увеличения выходного напряжения по показаниям вольтметра.
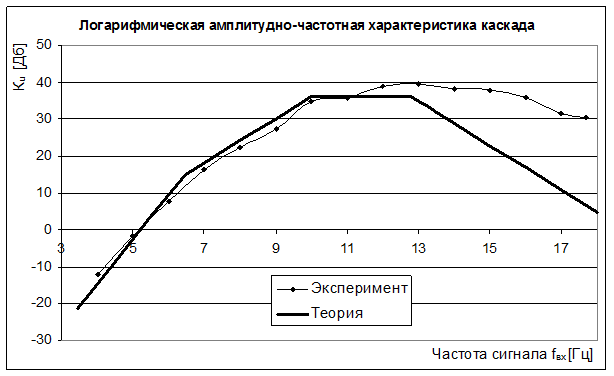
Частотная характеристика транзистора по форме и наклону соответствующих участков достаточно хорошо согласуется с теорией, но реальная ЛАЧХ лежит явно правее расчетной. Данное расхождение можно объяснить неправильным нахождением частоты fн2, которая меньше реальной. Причиной этого может являться погрешности использованного конденсатора Cp2. Увеличение емкости приводит к сближению зависимостей.
Малая частота сигнала и присутствие на входе и выходе конденсаторов заставляет задуматься об их влиянии. Действительно, входное сопротивление каскада для малых частот оказывается выше, что может приводит к смещению характеристики вправо.
Расхождение в правой части ЛАЧХ объясняется тем, что граничная частота транзистора указана с запасом и потому предельная частота работы транзистора и каскада в целом оказывается больше. Из-за этого правая точка перегиба имеет большую частоту, чет расчетная. Спад ЛАЧХ представлен всего несколькими точками, но по ним можно сказать, что наклон спада похож на расчетные 6Дб/окт.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.