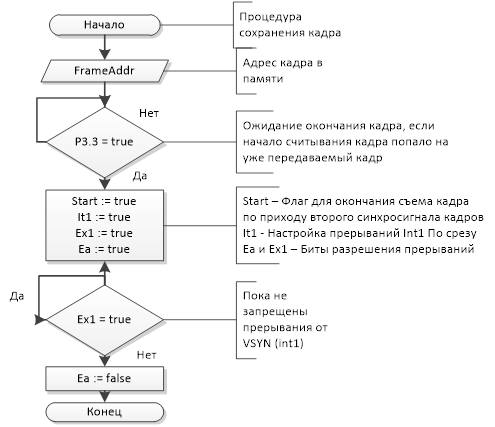
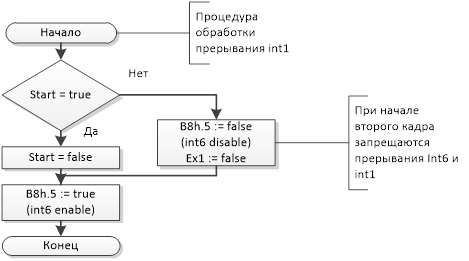
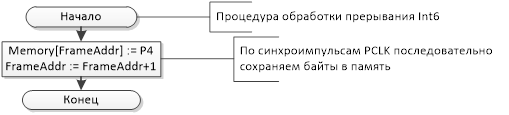
Общий текст программного обеспечения нижнего уровня приведен в приложении.
4. Анализ задания
Массив с изображением хранится во внешней памяти микроконтроллера по адресам 9C00h-FF00h. В каждом байте указанного диапазона содержится значение, отвечающее за глубину цвета RED палитры RGB (FFh – ярко-красный цвет, 0h - черный). Изначально в массиве все байты имеют значение 0h. По заданию преподавателя выбирается байт (точка на фрейме), который нужно повернуть на заданный угол относительно центра картинки.
Для того, чтобы реализовать поворот точки с заданными координатами относительно центра, необходимо разделить фрейм на координатную плоскость с 0й точкой посередине. Таким образом, после этого преобразования образуется 4 четверти(см. рис.1a).
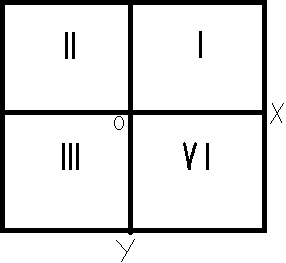
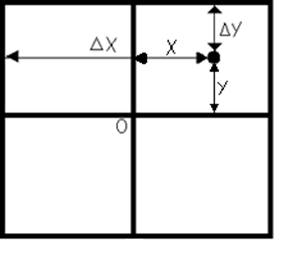
а) б)
Рис.1 a) Фрейм, б) Исходная точка
Тогда расположение заданной точки (рис.1б) в памяти будет определяться следующим выражением:
![]() (1)
(1)
Предположим, что нам нужно повернуть точку с координатами x,y(50;30) в I четверти на 30 градусов относительно начала координат против часовой стрелки. Чтобы решить эту задачу, можно воспользоваться теоремой косинусов. На рис. 2 точка А – исходная, а В – сдвинутая на 30 градусов. Чтобы узнать координату новой точки, нужно, чтобы был известен косинус начальный угол и гипотенуза (т.е. расстояние от центра до точки А).
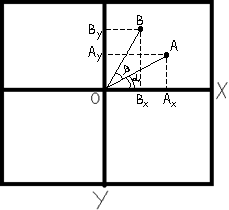
Рис. 2.А – начальная точка, В – сдвинутая на 30 градусов.
a) Определяем значение tg (или ctg) угла между заданной точкой и осью х (у). Для этого делим координаты точки друг на друга (x на y или y на x) в зависимости от того, какая координата меньше. Далее, имея значение тригонометрической функции, находим наиболее близкое значение угла между заданной точкой и осью х (у), используя массив значений углов tg (или ctg), заданных таблично, от 0 до 90 градусов. Для повышения точности вычислений, значение тригонометрических функций каждого угла представлены массивами 2х-байтовых чисел.
![]()
б) К полученному значению начального угла прибавляем угол, на который нужно повернуть точку и получаем результирующий угол поворота:
![]()
в) Далее находим гипотенузу: координату по x делим на cos начального угла:
![]()
г) Наконец, определяем координату, умножив cos или sin(в зависимости от того, ищем ли мы новую координату по х или по у, и в зависимости от четверти) на гипотенузу.
1-3 четверти:cos(![]() )*gipoten=new_x;
sin(
)*gipoten=new_x;
sin(![]() )*gipoten=new_y
)*gipoten=new_y
2-4 четверти: sin(![]() )*gipoten=new_x;
cos(
)*gipoten=new_x;
cos(![]() )*gipoten=new_y
)*gipoten=new_y
И рассчитываем ячейку в памяти, в которой должна оказаться эта точка:
1четверть: (0Y - ![]() )*176
+ 88 +
)*176
+ 88 + ![]()
2четверть: (0Y - ![]() )*176
+ 88 -
)*176
+ 88 - ![]()
3четверть: (0Y + ![]() )*176
+ 88 -
)*176
+ 88 - ![]()
4четверть: (0Y + ![]() )*176
+ 88 +
)*176
+ 88 + ![]()
е) Чтобы отметить эту точку на фрейме, преобразуем полученные координаты в память с помощью выражения 1 и записываем FFh в байт с полученным адресом. Однако, необходимо учесть, что при данном преобразовании не учитываются значения 0х координат. То есть для расчетов принимаются начальные координаты по х и по у, равные 0, но т.к. фрейм имеет четные размеры (176х144), то получается, что реальные значения осей начинаются с 1. Таким образом, чтобы избежать погрешности при вычислении положения новой точки в памяти, нужно вести вычисления с увеличенными координатами х и у на 1:
![]() (2)
(2)
5. Алгоритм программы
На рис.3 изображен основной алгоритм программы, а далее представлены алгоритмы отдельных блоков.
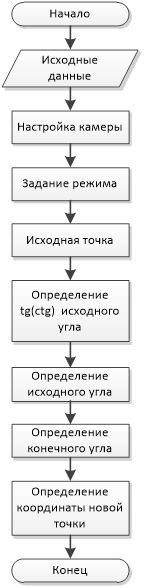
Рис. 3. Общий алгоритм программы
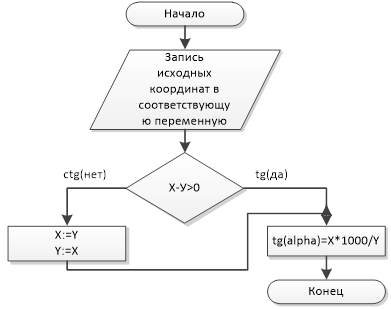
Рис. 4. Определение tg(ctg) начального угла
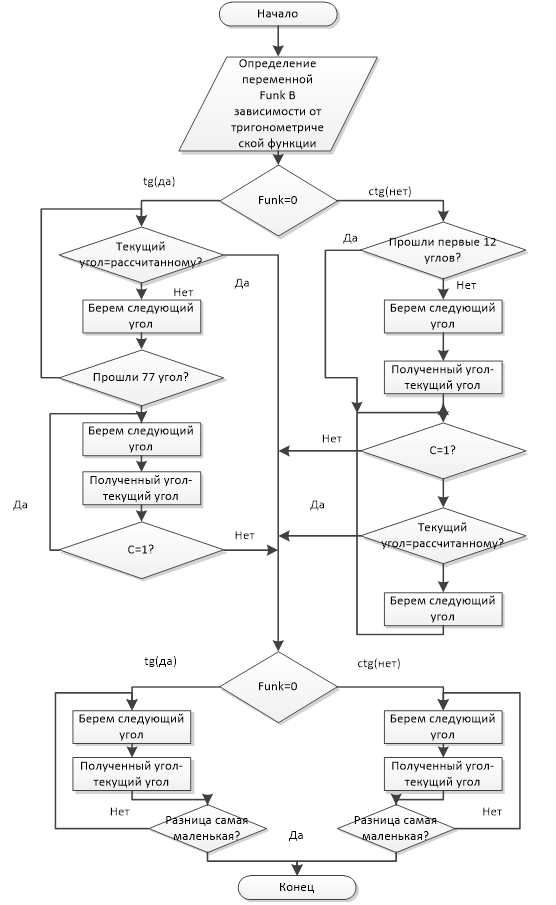
Рис. 5. Определение угла из массивов тригонометрических функций
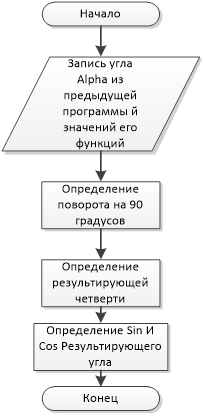
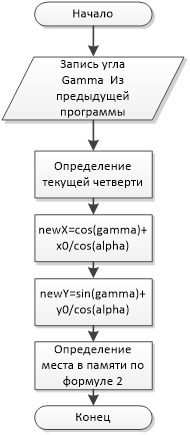
Рис. 6. Определение конечного угла Рис. 7. Определение координат конечной точки
6. Текст программы
chetvert: equ 46h ; четверть, в которой находится точка
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.