Информатика и выч. техника \ Алгоритмизация задач управления

Моделирование объектов систем компьютерного управления, сбор и фиксация результатов моделирования. Изучение методики моделирования непрерывных объектов на аналоговом вычислительном комплексе

Страницы работы

17 страниц (Word-файл)

Скачать файл

Фрагмент текста работы

Санкт-Петербургский Государственный Политехнический Университет

Факультет Технической Кибернетики

Кафедра Компьютерные Системы и Программные Технологии

О Т Ч Ё Т

о лабораторной работе

«Моделирование объектов систем компьютерного управления, сбор и фиксация результатов моделирования.»

Выполнили:

гр. 4081/11 А

Преподаватель:

Санкт-Петербург

2011 г

1. Цель Работы.

· Изучение методики моделирования непрерывных объектов на аналоговом вычислительном комплексе.

· Знакомство с организацией системы сбора информации на базе платы сопряжения L-154 и персонального компьютера.

· Оценка точности моделирования объектов управления средствами аналоговой вычислительной техники.

2. Методика моделирования

Методика строится на использовании основных положений теории математического подобия, позволяющей установить подобие физических процессов в аналоговой модели и объекте. Программирование решения этих зависимостей на АВК заключается в создании схем, состоящих из ОУ и вспомогательных элементов так, чтобы физические процесс в них описывались математическими зависимостями.

1) Составление схемы набора решающих элементов, обеспечивающей преобразование «машинных переменных» в соответствии с исходной математической зависимостью, описывающей поведение моделируемого объекта. («Качественное подобие»).

2) Установление количественных зависимостей между исходными и машинными переменными, а также определение значения коэффициентов передач решающих элементов.

3. Схема набора и расчет ее параметров

В данной лабораторной работе рассматривается объект, заданный линейным дифференциальным уравнением второго порядка:

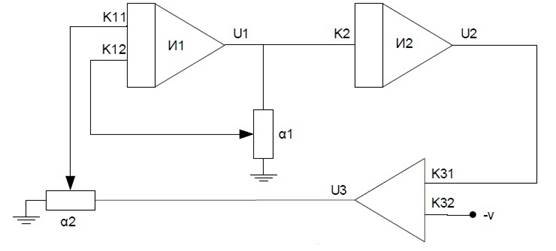
Рис 1. Схема набора.

Составим машинные уравнения:

Где:

Тогда дифференциальное уравнение в машинной записи будет выглядеть так:

Сопоставив это уравнение с исходным, сможем найти соотношения их коэффициентов:

Зададим , тогда:

4. Проведение эксперимента

Исходные значения:

a₀ = 2.5

b = 2.5

a₂ = 1

Значение коэффициента, соответствующее точке бифуркации:

a_бф = =3,1622

4.1 Коэффициент a₁ = 0, начальные условия x(0) = 2 x’(0) = 0, внешнее воздействие c = 0.

Аналитическое решение:

В дальнейшем для построения теоретических зависимостей будет использоваться скрипт для программы MATLAB, текст скрипта приведён в Приложении 1.

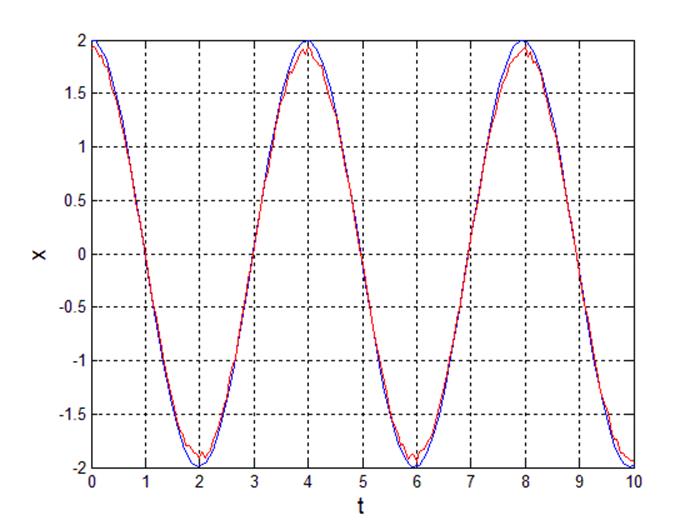
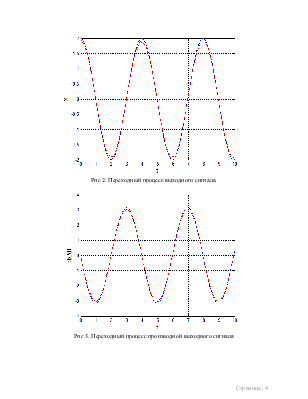
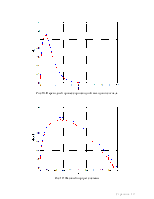
Рис 2. Переходный процесс выходного сигнала.

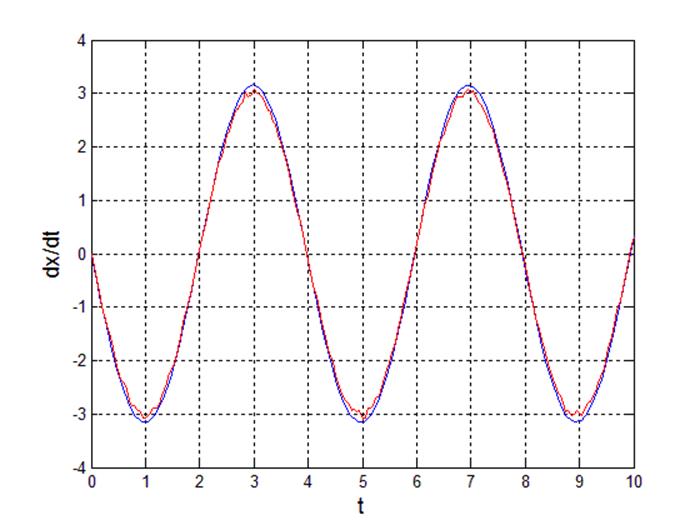
Рис 3. Переходный процесс производной выходного сигнала

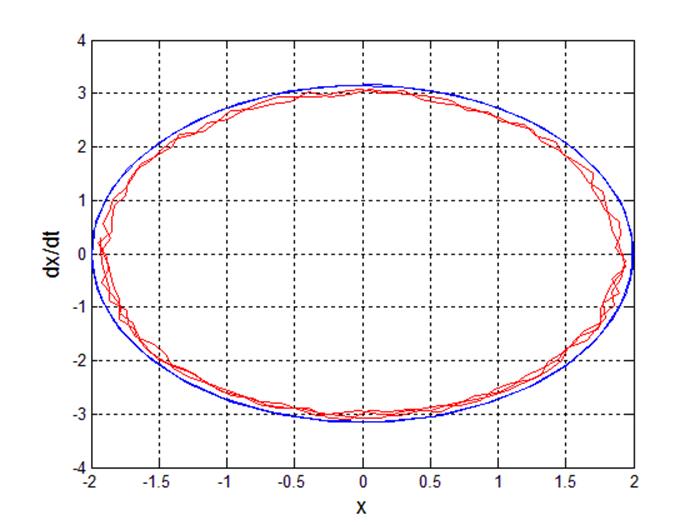
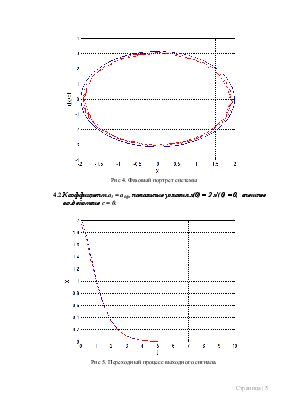
Рис 4. Фазовый портрет системы

4.2 Коэффициент a₁ = a_бф, начальные условия x(0) = 2 x’(0) = 0, внешнее воздействие c = 0.

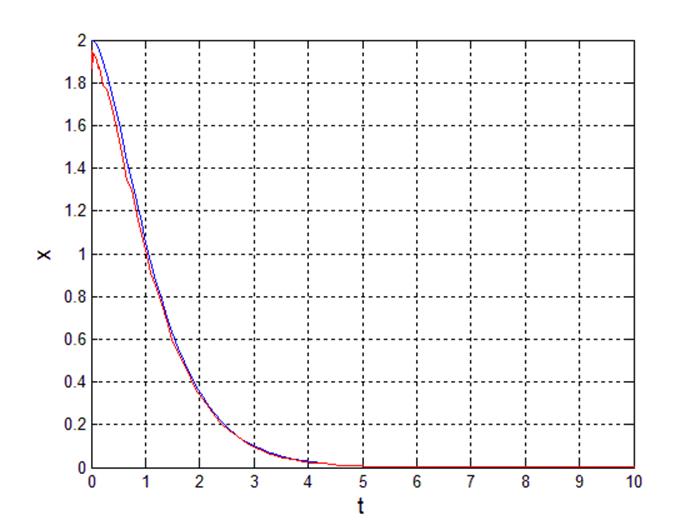
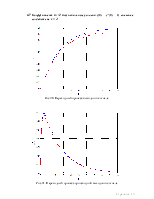
Рис 5. Переходный процесс выходного сигнала.

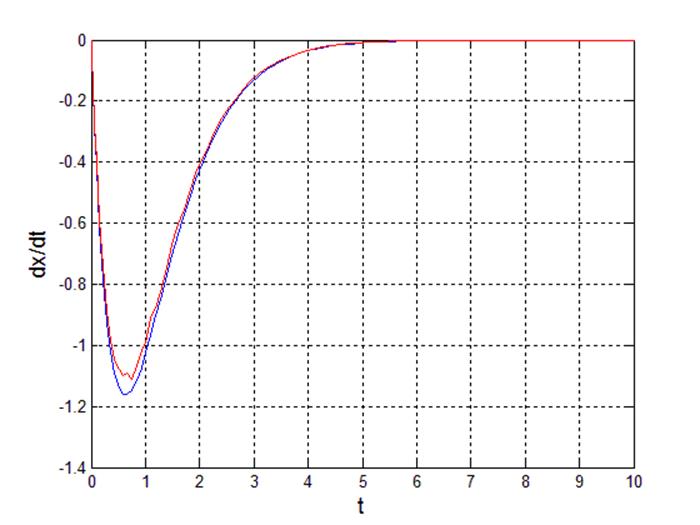
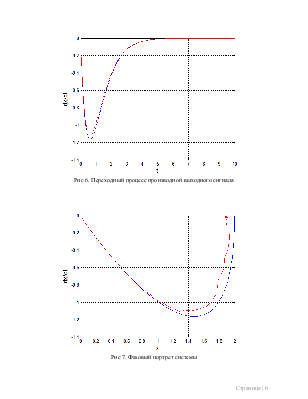
Рис 6. Переходный процесс производной выходного сигнала

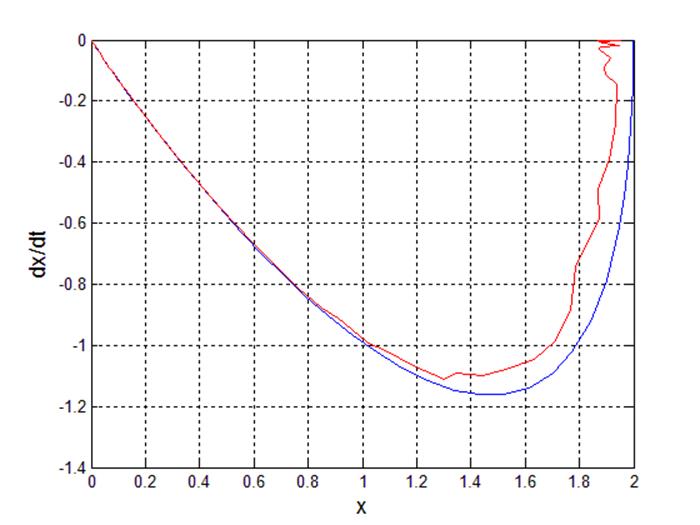
Рис 7. Фазовый портрет системы

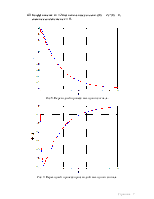
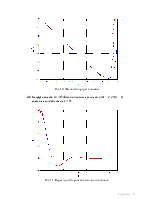
4.3 Коэффициент a₁ = 2a_бф, начальные условия x(0) = 2 x’(0) = 0, внешнее воздействие c = 0.

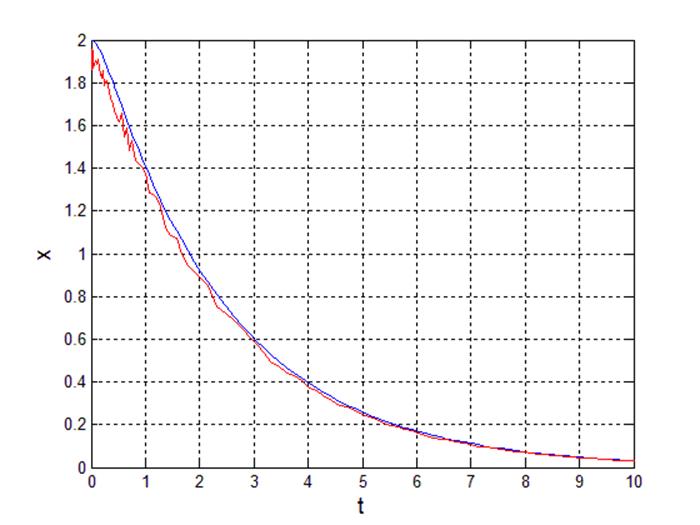
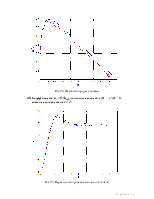
Рис 8. Переходный процесс выходного сигнала.

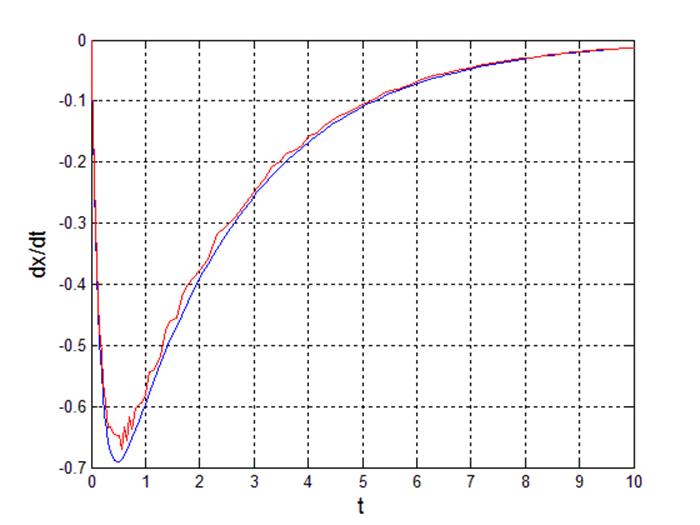
Рис 9. Переходный процесс производной выходного сигнала

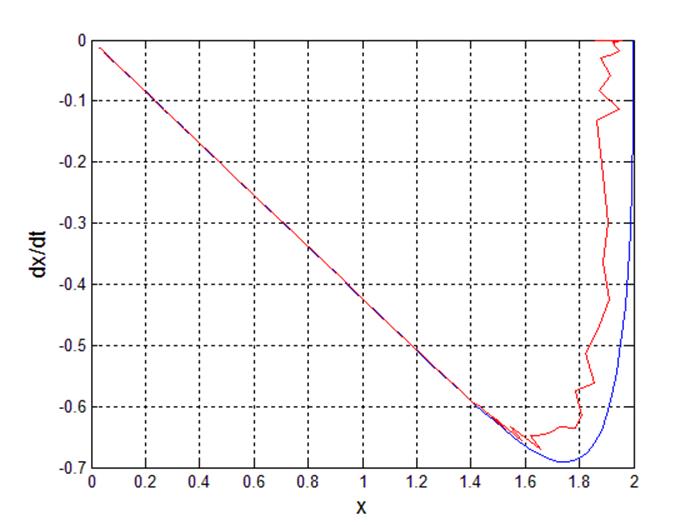
Рис 10. Фазовый портрет системы

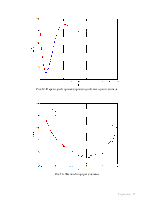
4.4 Коэффициент a₁ = 0,5a_бф, начальные условия x(0) = 2 x’(0) = 0, внешнее воздействие c = 0.

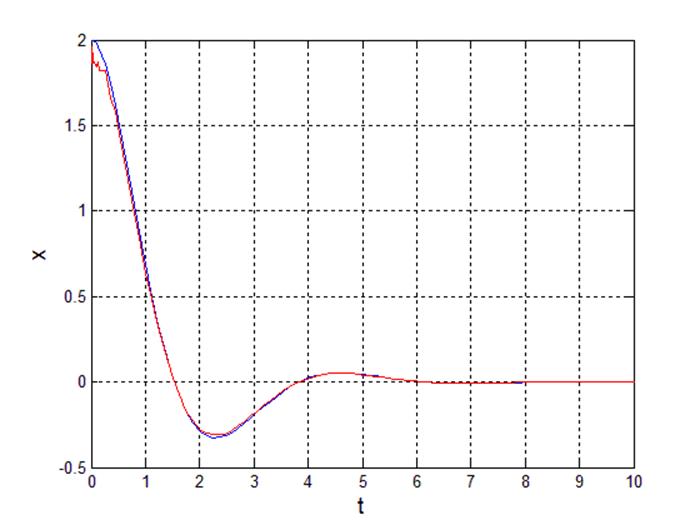
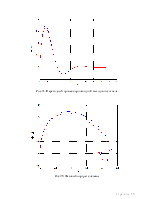
Рис 11. Переходный процесс выходного сигнала.

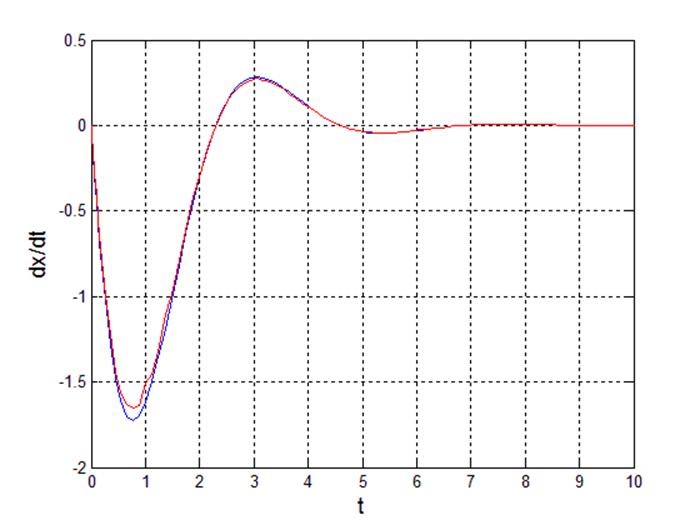
Рис 12. Переходный процесс производной выходного сигнала

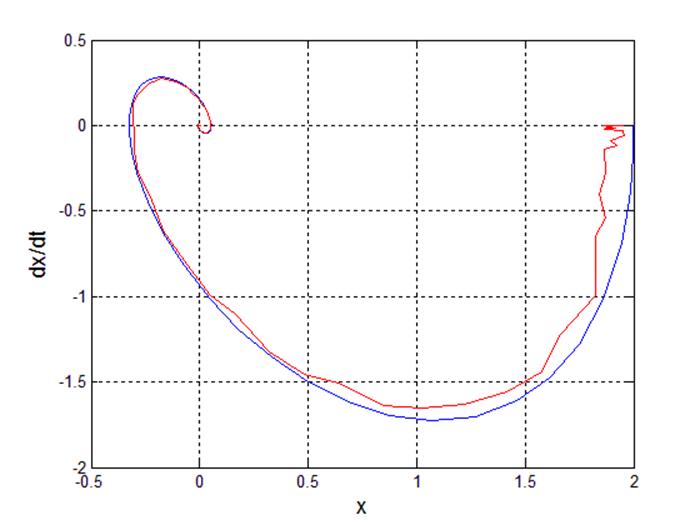
Рис 13. Фазовый портрет системы

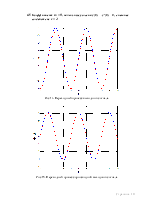
4.5 Коэффициент a₁ = 0, начальные условия x(0) = x’(0) = 0, внешнее воздействие c = 2.

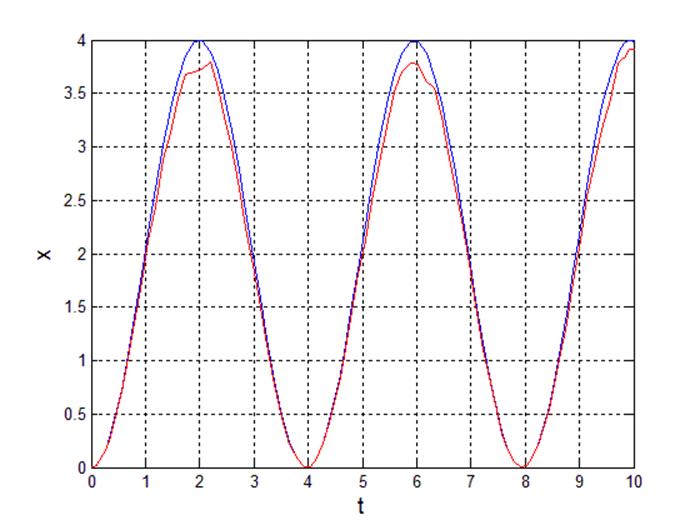
Рис 14. Переходный процесс выходного сигнала.

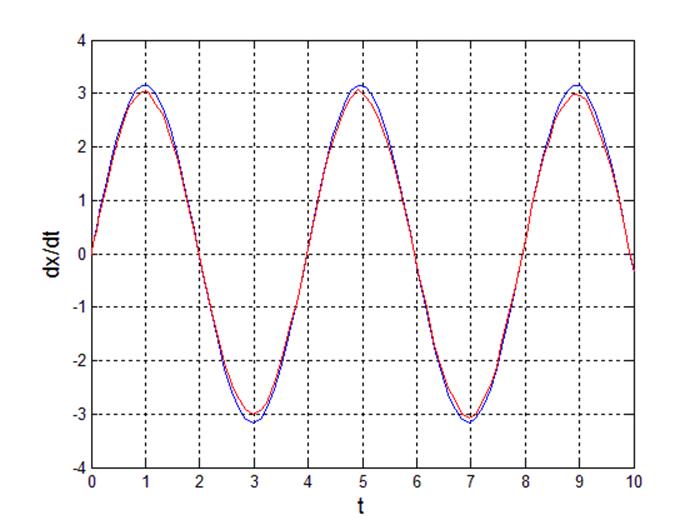
Рис 15. Переходный процесс производной выходного сигнала

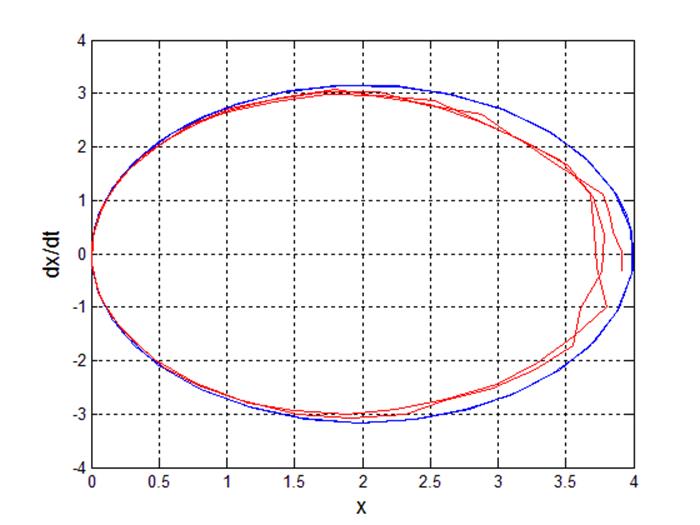
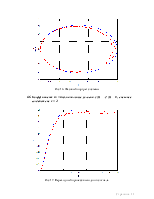
Рис 16. Фазовый портрет системы

4.6 Коэффициент a₁ = a_бф, начальные условия x(0) = x’(0) = 0, внешнее воздействие c = 2.

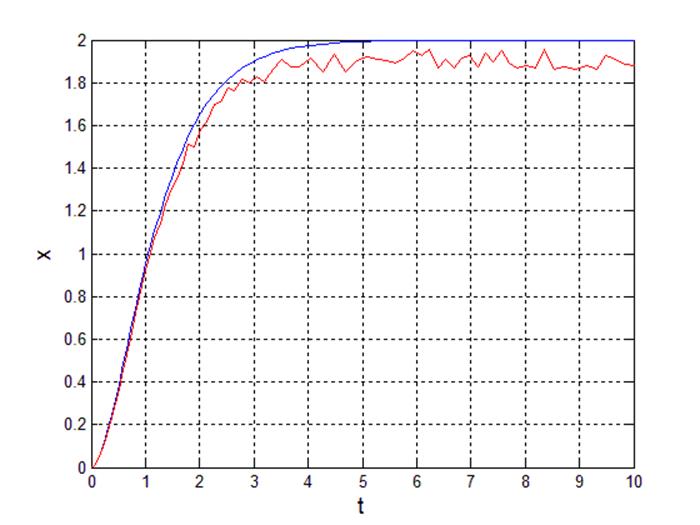
Рис 17. Переходный процесс выходного сигнала.

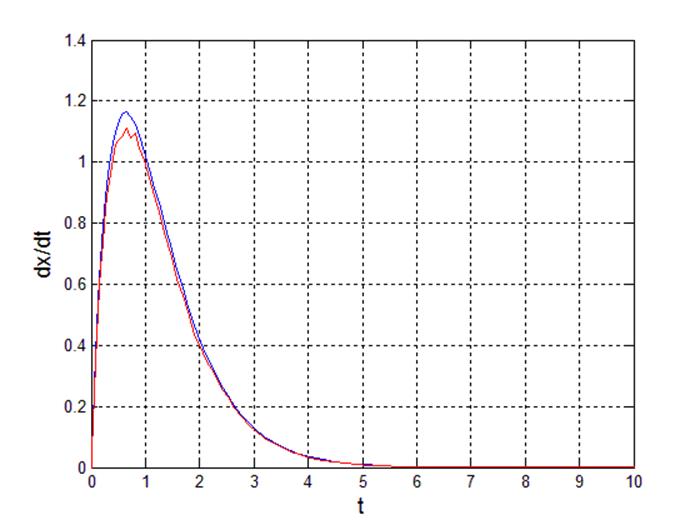
Рис 18. Переходный процесс производной выходного сигнала

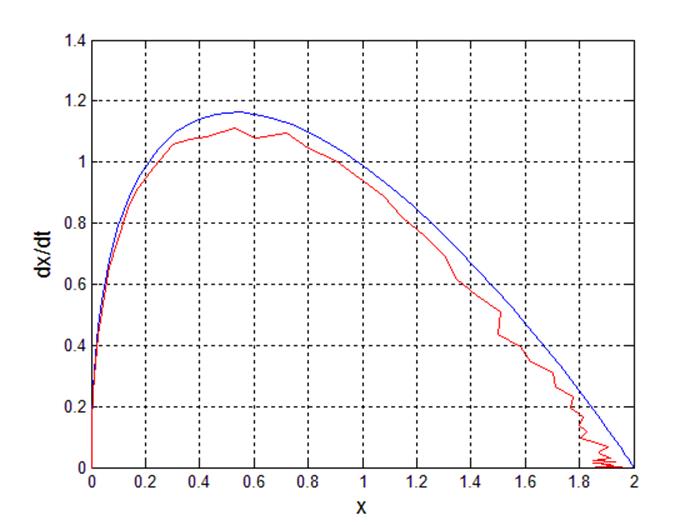
Рис 19. Фазовый портрет системы

4.7 Коэффициент a₁ =2 a_бф, начальные условия x(0) = x’(0) = 0, внешнее воздействие c = 2.

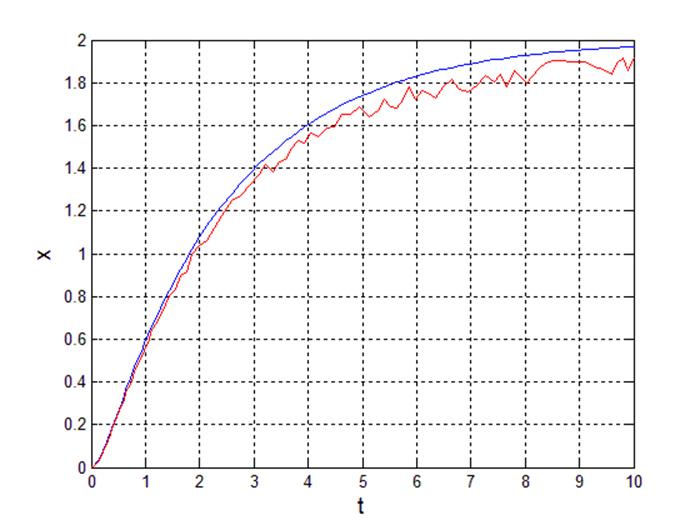
Рис 20. Переходный процесс выходного сигнала.

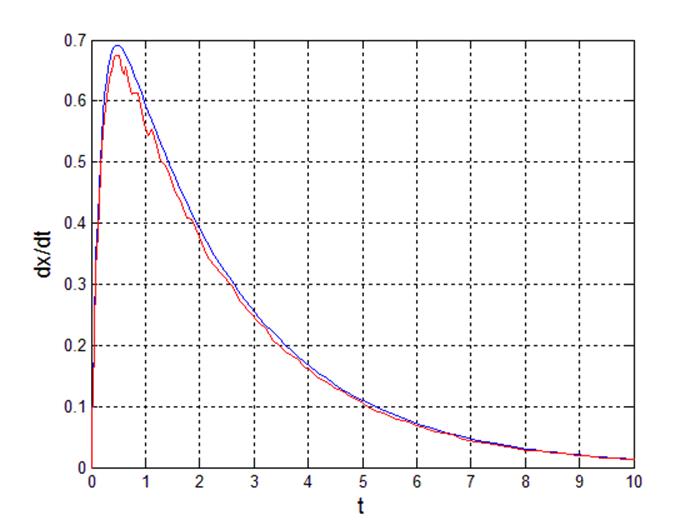
Рис 21. Переходный процесс производной выходного сигнала

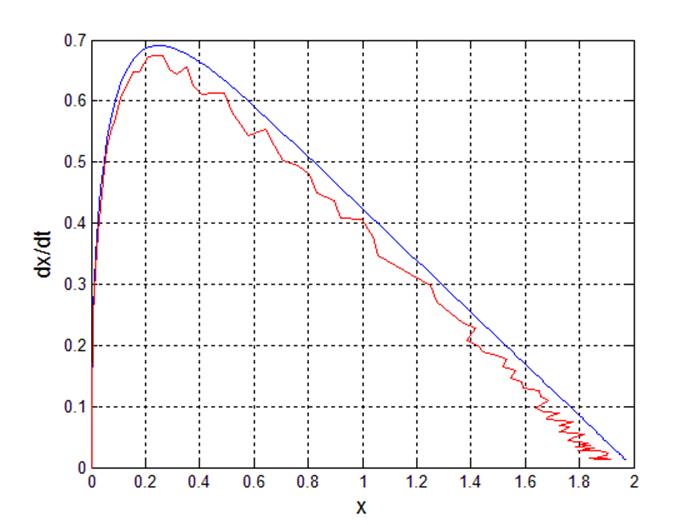
Рис 22. Фазовый портрет системы

4.8 Коэффициент a₁ = 0,5a_бф, начальные условия x(0) = x’(0) = 0, внешнее воздействие c = 2.

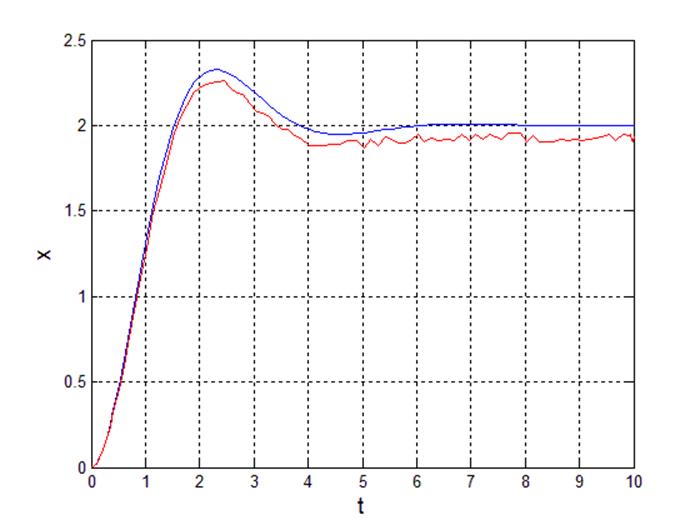
Рис 23. Переходный процесс выходного сигнала.

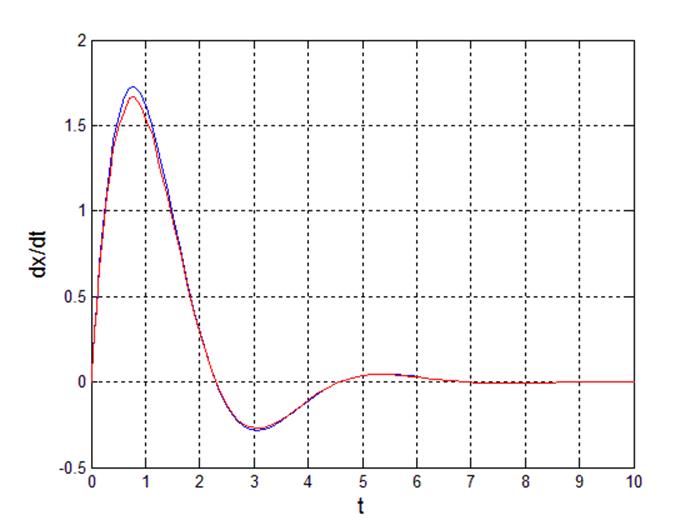
Рис 24. Переходный процесс производной выходного сигнала

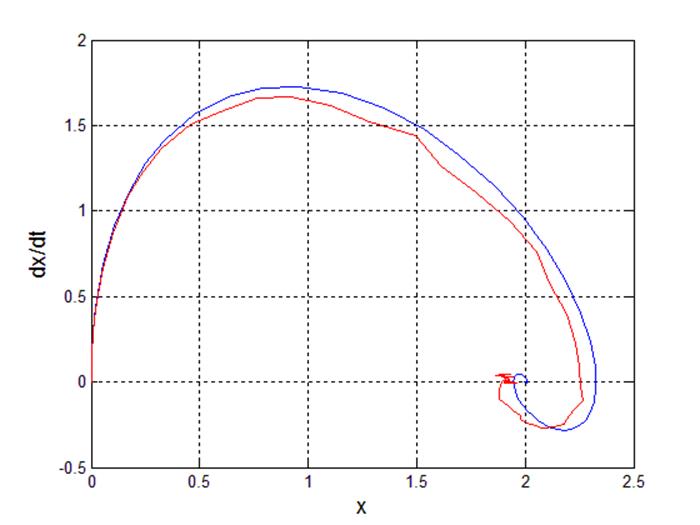
Рис 25. Фазовый портрет системы

5. ПРИЛОЖЕНИе 1.

function Main( )

% Коэффициенты дифференциального уравнения

global b;

global a0;

global a1;

global a2;

% Возмущающее воздействие

global c;

a0 = 2.5; % Коэффициент A0

b = 2.5; % Коэффициент B

a2 = 1; % Коэффициент A2

c = 2; % Внешнее воздействие

a1bf = 2*sqrt( a0 ); % Точка бифуркации

a1 = 0.5*a1bf; % Коэффициент A2

% Время моделирования

t0 = 0; tf = 10;

% Начальные условия

x0 = 0;

dxdt0 = 0;

% Решение уравнения

[ t, X ] = ode45( 'fun_du', [t0 tf] , [ x0; dxdt0 ]);

%%%%%%%%%%% Переходный процесс x(t) %%%%%%%%%%%

hFigure1 = figure('Color',[1 1 1]);

hAxes1 = axes('Visible','on','Parent',hFigure1);

box('on');

hold('all');

grid on;

xlabel( hAxes1, 't','FontSize',13); ylabel(hAxes1, 'x','FontSize',13);

hPlot1 = plot( t, X(:,1) );

set( hPlot1, 'color','b', 'LineWidth', 1)

%%%%%%%%%%% Переходный процесс по производной %%%%%%%%%%%

hFigure2 = figure('Color',[1 1 1]);

hAxes2 = axes('Visible','on','Parent',hFigure2);

box('on');

hold('all');

grid on;

xlabel(hAxes2, 't','FontSize',13); ylabel(hAxes2, 'dx/dt','FontSize',13);

hPlot2 = plot( t, X(:,2) );

set( hPlot2, 'color','b', 'LineWidth', 1)

%%%%%%%%%%% Фазовые траектории %%%%%%%%%%%

hFigure3 = figure('Color',[1 1 1]);

hAxes3 = axes('Visible','on','Parent',hFigure3);

box('on');

hold('all');

grid on;

xlabel( hAxes3, 'x','FontSize',13); ylabel(hAxes3,'dx/dt', 'FontSize',13);

hPlot3 = plot( X(:,1), X(:,2) );

set( hPlot3, 'color','b', 'LineWidth', 1);

end

function dXdt = fun_du( t, X )

global b;

global c;

global a0;

global a1;

global a2;

x = X(1);

y = X(2);

dXdt = [ y;

(1/a2)*(b*c - a1*y - a0*x ) ];

end

6. ВЫВОДЫ

Экспериментальные результаты моделирования объекта, описываемого линейным дифференциальным уравнением второго порядка, с помощью стенда АВК-31наглядно показали достаточную точность вычислений. Расхождение теоретических и практических значений может быть вызвано отклонением номинала аналоговых величин.

Характер переходного процесса зависит от коэффициентов уравнения:

· при a₀=0 наступают незатухающие колебания;

· при a₀=0,5a_бф процесс имеет малую степень колебательности;

· при увеличении коэффициента увеличивается быстродействие, и процесс