Модуляция сигналов. Понятие модуляции. Амплитудная модуляция. Условная модуляция. Спектры сигналов УМ, страница 2

 - неизменная часть начальной фазы.

 - модуляционная функция.

ФМ-сигнал аналитически представляется:

                                          (12)

Амплитуда ФМ-сигнала неизменна, а фазовый угол изменяется во времени.

При гармонической модуляции:

                           (13)

ФМ-сигнал может быть записан:

                                             (14)

 - индекс ФМ или девиация фазы.

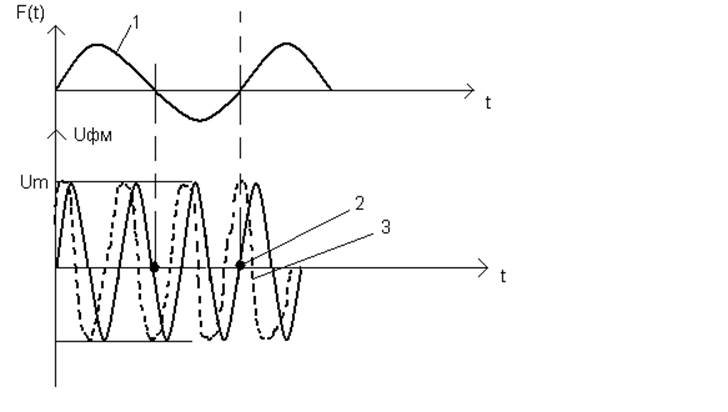
Рисунок 4.

1 – низкочастотный модулированный сигнал.

2 – немодулированный гармонический сигнал.

3 – ФМ-сигнал.

Частотная модуляция.

Модулирующий сигнал F(t) воздействует на частоту колебания.

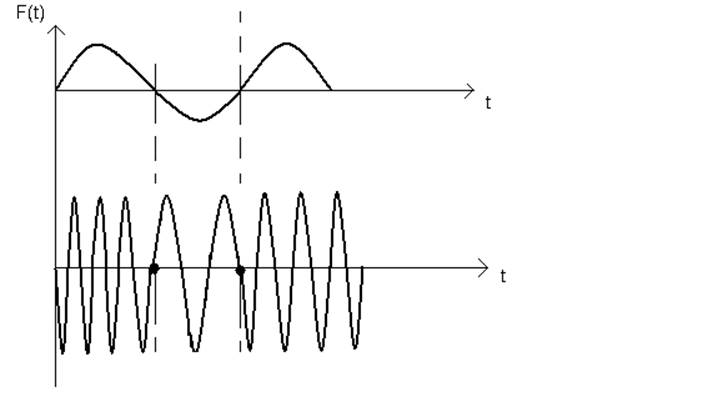
Рисунок 5.

                                                                                                (15)

 - мгновенная циклическая частота.

                                                                                                          (16)

 

 

С другой стороны:

                                                                                      (17)

Тогда подставим (15) и (17) в (12) и получим выражение для ЧМ-сигнала:

        (18)

При однотональной гармонической модуляции:

 

 

Для УМ окончательно получим:

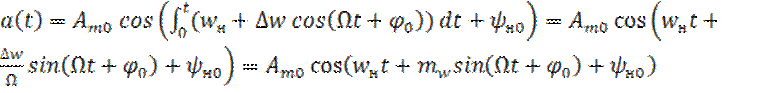              (19)

В сравнении выражения (14) и (19) показывают единство явления угловой модуляции.

При ФМ и ЧМ фаза колебаний меняется, но в соотношении между фазовым углом и модулированным сигналом различна.

Для ФМ:

 

                                          (20)

Для ЧМ:

                               (21)

                                                                                      (22)

Начальная фаза пропорциональна интегралу от модулированного сигнала.

Если колебания модулированы по фазе сигналом, предварительно прошедшим через интеграл, то получим колебания, индуцированные исходным сигналом.

Повышение экономичности передатчиков за счет полного использования мощности.

Будем рассматривать простейший случай угловой модуляции напряжения для ЧМ и для ФМ. Выражения (12) и (19) можно свести к такому виду:

                                                 (23)

m= - для ЧМ.

m= – для ФМ.

Сигналы с угловой модуляцией могут быть представлены в виде функции Бесселя первого рода n-порядка , аргументами которых являются индексы m():

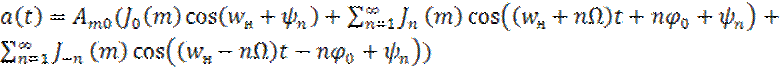                                                    (24)

Из (24) следует, спектры ЧМ- и ФМ-сигналов даже в случае простейшей гармонической модуляции имеют бесконечное число гармоник, образующих верхние и нижние боковые полосы с частотами  и  соответственно (в АМ-сигнале имеют место лишь 2 боковые гармоники) (рисунок 6):

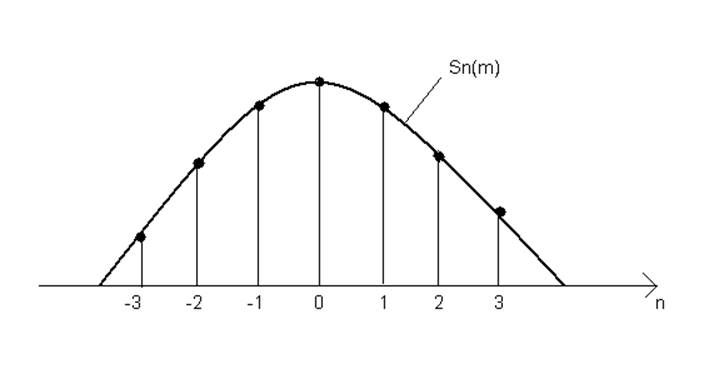
m=1

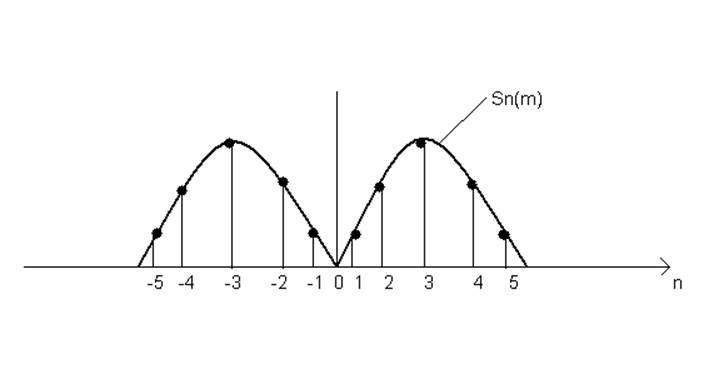
m=3

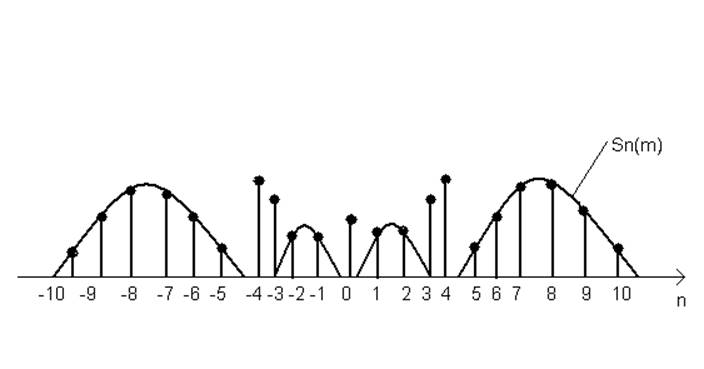
Рисунок 6.

Амплитуда каждой гармоники с частотой  или  в спектре ЧМ- и ФМ-сигналов определяется абсолютным значением функции Бесселя n-порядка с аргументом n . Амплитуды гармоник изменяются в зависимости от индекса модуляции m. Из рисунка 6 следует, что с увеличением индекса m порядок гармоник с максимальной амплитудой растет, стремясь к величине m (n→m). При этом гармоники высшего порядка возрастают. С увеличением m энергия модулированного сигнала сосредотачивается на гармониках высшего порядка.

Простые количественные изменения m пропорционального модулированному сигналу приводит к значительным качественным изменениям спектра.

Спектр сигнала при УМ бесконечен. Но в связи с тем, что при фиксированном m значение функции Бесселя быстро уменьшаются с ростом показателей n, то гармониками с порядковым номером n>m+1= в разложении по (24) можно пренебречь.

Ширина спектра УМ-сигнала равна:

                                                                             (25)

При m>>1:

                                                                                                          (26)

Ширина спектра при УМ определяется девиацией фазы (ФМ) или частоты (ЧМ).

При УМ с малыми индексами (m<<1) – когда узкополосная ЧМ, ширина спектра определяется так:

                                                                                                              (27)

То есть в спектре ЧМ-сигнала присутствует вместо боковых полос только пара боковых гармоник.

Ширина ЧМ спектра совпадает с шириной ФМ спектра.

Разница в спектрах ЧМ и АМ возрастает при больших индексах .

Например, в радиовещании ЧМ пусть , поэтому .

Ширина спектра по (26):

1) В случае АМ:

 

При равных условиях спектр ЧМ в 75 раз шире, чем спектр АМ-сигнала (). Передача широкополосных ЧМ и ФМ-сигналов возможна в диапазоне УКВ (f=30…300мГц).

Сравнение спектров ЧМ и ФМ.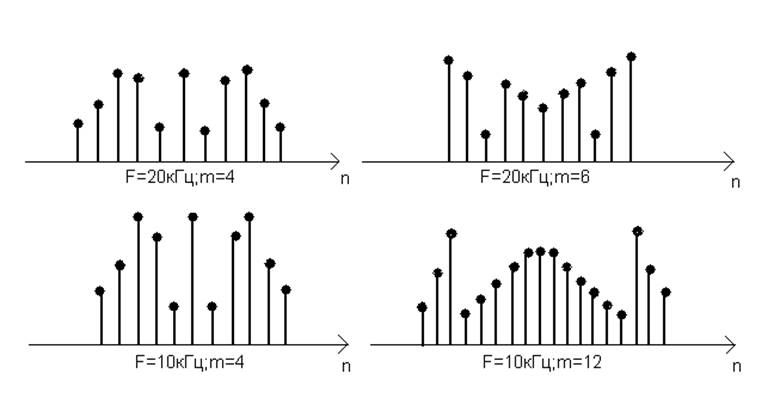

Рисунок 7.

1) При одинаковых , Ώ, m ЧМ и ФМ спектры ничем не отличаются друг от друга. Изменение  и m вызывают одинаковые изменения в ФМ и ЧМ спектрах.

2) Спектр ЧМ-сигнала в отношении ширины не зависит от частоты модуляции:

 

 

При уменьшении  расстояние между спектральными линиями уменьшается, но так как увеличивается m, то растет число учитываемых гармоник (рисунок 6). И следовательно, ширина ЧМ спектра практически не меняется.

3) Спектр ФМ-сигнала в отношении ширины от частоты не зависит. Индекс модуляции  от Ώ не зависит. Поэтому при уменьшении Ώ число учитываемых гармоник не изменяется, по ширине спектра уменьшается:

 

Следовательно, преимущество ЧМ перед ФМ состоит в большом постоянстве спектров сигналов.