Математические модели сигналов. Динамическое представление сигналов (ДПС) с помощью функций включения и дельта-функций

Лекция 2

Математические модели сигналов

1. Динамическое представление сигналов (ДПС) с помощью функций включения и дельта-функций.

2. Геометрические методы в теории сигналов.

1. Любой реальный сигнал может с целью анализа быть представлен суммой двух элементарных сигналов, возникающие в последние моменты времени.

Если длительность сигнала стремится к нулю, то в пределе получим точное представление сигнала – в этом и состоит динамическое представление сигнала.

Существует 2 основных способа ДПС:

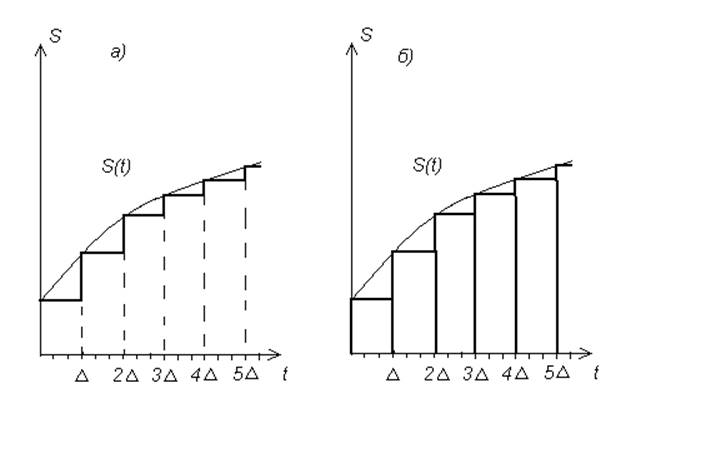
Рисунок 1

а) ДПС с помощью элементарной функции включения.

Б) ДПС с помощью элементарно примыкающих друг к другу импульсов.

При таком ДПС при ∆→0 последовательность функций включения или элементарных импульсов будет все точнее воспроизводить исходный непрерывный сигнал S(t).

Функция включения: пусть дана следующая функция

V(t)=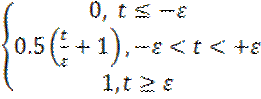                                                                       (1)

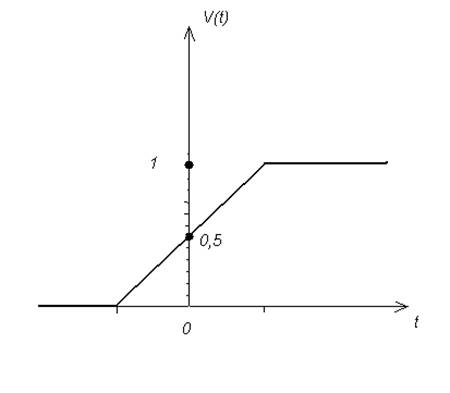
Рисунок 2

Если ε→0, то переход функции V(t) из нулевого в единичное состояние будет происходить мгновенно.

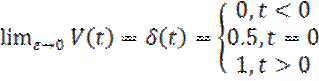                                                                        (2)

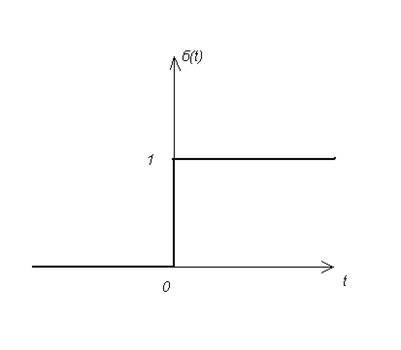
Рисунок 3

Функция  - функция включения или функция Хэвисайда, единичная ступенчатая функция. С помощью этой функции удобно рассматривать разнообразные цепи в электрических цепях. Часто используется смещенная функция включения.

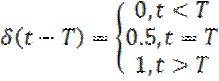                                                                                (3)

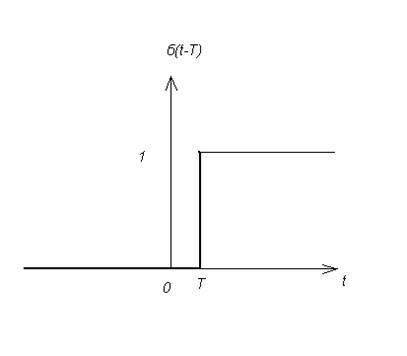
Рисунок 4

ДПС с помощью функций включения: пусть дан некоторый сигнал S(t), причем S(t)=0, при t<0. Пусть:{∆, 2∆, 3∆, 4∆, 5∆, …} – последовательность моментов времени, а множество {S₁, S₂, S₃, S₄, …} – соответствующая им последовательность значения сигнала.

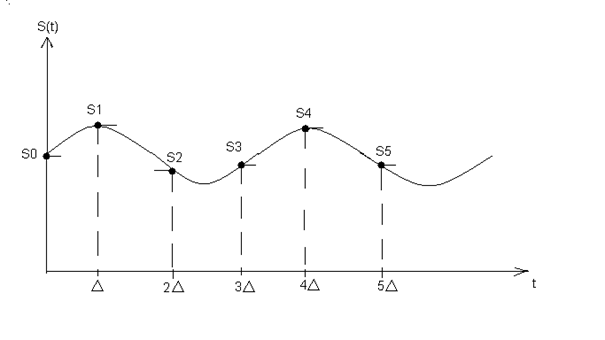
Рисунок 5

S₀ – S в нуле: S₀=S(0) – начальное значение сигнала, тогда S(t) можно представить при любом времени суммой функций включения:

S(t)≈S₀δ(t)+(S₁-S₀)δ(t-∆)+(S₂-S₁)δ(t-2∆)+…= S₀δ(t)+

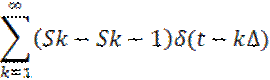                                                                                                (4)

Если теперь ∆→0, то k∆→δ. Малые приращения сигнала (S_k-S_k-1)→dS.

Тогда ДПС обретет следующий вид:

                                                                            (5)

Произвольный сигнал может быть представлен формулой (5).

Дельта-функция.

Пусть имеем прямоугольный импульс заданный зависимостью:

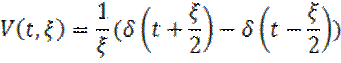                                                                            (6)

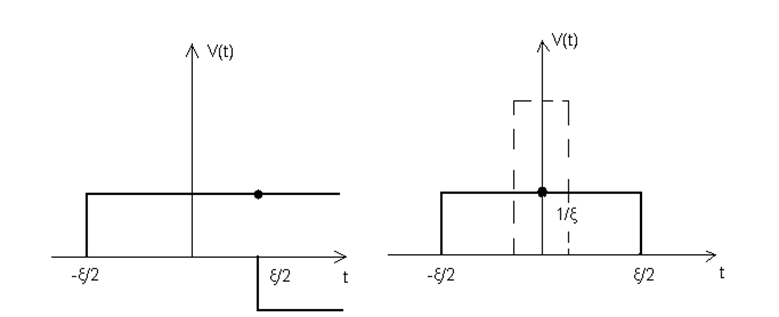
Рисунок 6

Он характеризуется тем, что при любом ξ его площадь равна 1:

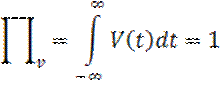
Если ξ→0, то импульс V(t) будет уменьшатся по длительности, однако его площадь неизменна, то амплитуда импульса 1/ξ неограниченно возрастает, в пределе получим дельта-функцию или функцию Дирака (см. рисунок 7).

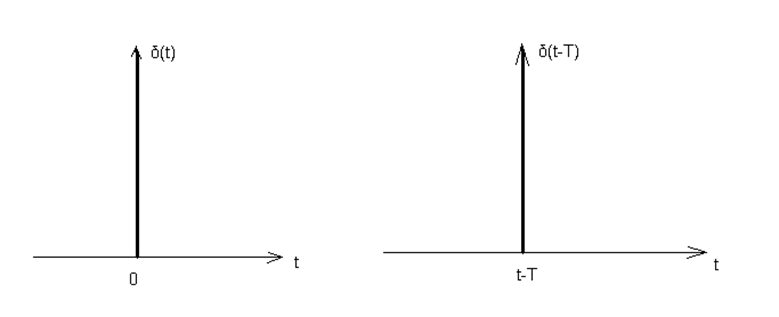
Рисунок 7

                                                                                             (7)

Функция Дирака – обобщенная функция, то есть она позволяет анализировать разрывные процессы, которые не доступные классическому анализу. Она сосредоточена в точке t=0, а ее интеграл:

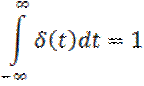                                                                                                      (8)

ДПС с помощью дельта-функций.

Элементарный импульс на рисунке 1,б) может быть представлен:

η_k = S_k(δ(t - t_k) - δ(t - t_k - ∆))                                                                             (9)

Исходный сигнал на 1,б) представлен как сумма сигналов:

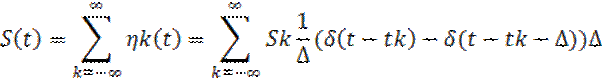
Получим формулу ДПС:

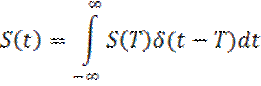                                                                                  (10)

Важное свойство дельта-функции: ее физическая размерность такая же как и у частоты.

Из (10) вытекает следующее свойство: если непрерывную функцию S(t) умножить на дельта-функцию и произведение проинтегрировать во времени, то результат равен значению непрерывной точки, где сосредоточен дельта-импульс.

Из этого свойства вытекает структурная схема мгновенных значений.

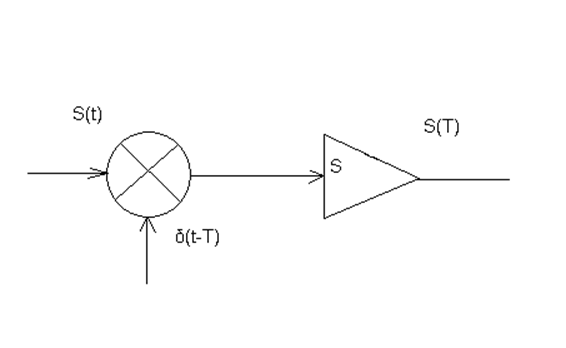
Рисунок 8