Спектральный анализ помех различной формы. Представление сигналов во временной области. Способы представления сигналов, методы перехода из одной формы представления в другую

Временное представление сигнала позволяет получить информацию не только о мгновенных значениях сигнала, но и о его поведении на всей временной оси как в "прошлом", так и в "будущем". Однако временное представление не дает информации о распределении энергии сигнала по частотному диапазону, что необходимо при анализе характера воздействия сигнала на конкретное микроэлектронное устройство.

Представление сигналов в частотной области

Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции. Значение гармонических сигналов для радиотехники обусловлено рядом причин:

   Гармонические сигналы инвариантны относительно преобразований, осуществляемых стационарными линейными электрическими цепями. Если такая цепь возбуждена источником гармонических колебаний, то сигнал на выходе цепи остается гармоническим с той же частотой, отличаясь от входного сигнала лишь амплитудой и начальной фазой.

  Техника генерирования гармонических сигналов относительно проста.

Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, то говорят, что осуществлено спектральное разложение этого сигнала. Отдельные гармонические компоненты сигнала образуют его спектр.

Спектральное разложение для периодического сигнала имеет вид:

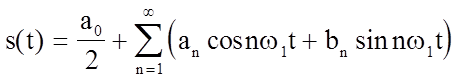
с коэффициентами

, 

,              .

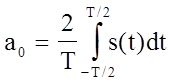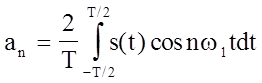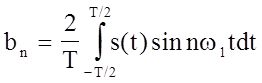В общем случае, периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами w_n=nw₁ (n=1,2,3,...), кратными основной частоте последовательности.

Преобразование Фурье для одиночного сигнала осуществляется по формуле

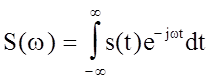
и носит название спектральной плотности сигнала.

Судить о распределении энергии сигнала по частотному диапазону можно по энергетическому спектру сигнала:

Энергия любого сигнала есть результат суммирования вкладов от различных интервалов частотной оси.

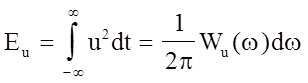
Рассмотрим энергетический спектр прямоугольного импульса.

Спектральная плотность прямоугольного видеоимпульса имеет вид:

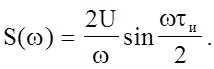
Энергетический спектр получим путем возведения в квадрат спектральной плотности:

.

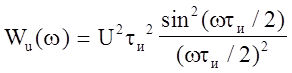Соответствующий график приведен на рис. 2.

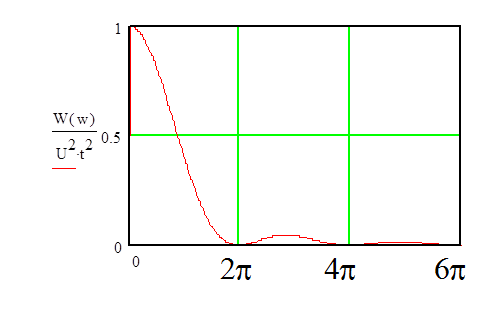
Рис. 2. Нормированный энергетический спектр прямоугольного видеоимпульса как функция безразмерной частотной переменной

Спектральный анализ помех

По оценкам специалистов в мире существует  порядка  200 различных стандартов по ЭМС,  в  том  числе  и  значительное число,  касающееся  испытаний  по  отношению  к   импульсным помехам. Международные усилия в области стандартизации привели к разработке стандарта IEC61000-4-4, который  состоит  из  пяти частей,  в  том  числе  три  из  них  касаются    импульсных испытаний, две - одиночными импульсами, третья - пачками. Эта часть стандарта  касается  испытаний  на  помехозащищенность пачками импульсов помех, которые  имеют  следующие  основные параметры:

·  форма импульса близка к экспоненциальной;

·  длительность фронта 5 нс;

·  длительность импульса на  уровне  половины  амплитуды импульса 50 нс;

·  длительность пачки импульсов 15 мс;

·  частота следования импульсов в пачке до 5 кГц;

·  количество импульсов в пачке 37 и 75.

Одиночный импульс МЭК

Определим спектральную функцию одиночного стандартизированного импульса МЭК, представленного формулой:

, где:

·  A- амплитуда импульса;

·  b1, b2 - коэффициенты наклона экспонент (b1 = 0.01742,b2 = 0.3051);

·  k - коэффициент крутизны:

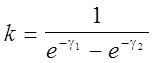  , где:

   ,  ,  .

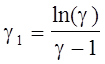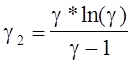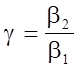Проинтегрируем функцию по t в интервале от 0 до t1=300 нс. Такой интервал выбран из соображений учета наибольшей энергии спектра импульса. Предел импульса 300 нс определен при анализе графика импульса МЭК как наиболее оптимальный. Спектральная функция определяется классическим способом при помощи преобразований Фурье

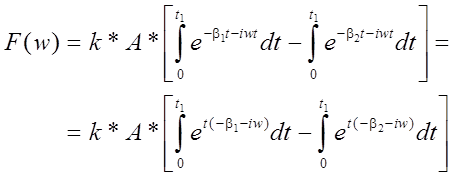
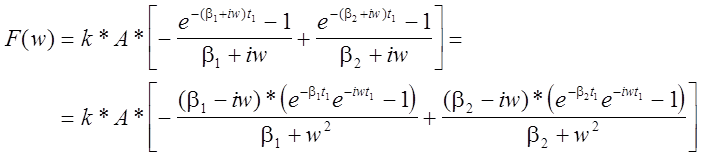Рассчитаем спектральную функцию в виде:

, где:

Q - реальная составляющая спектральной функции;

P - мнимая составляющая спектральной функции.

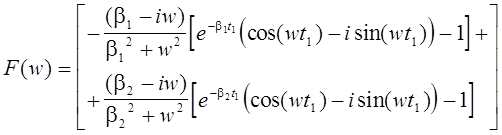
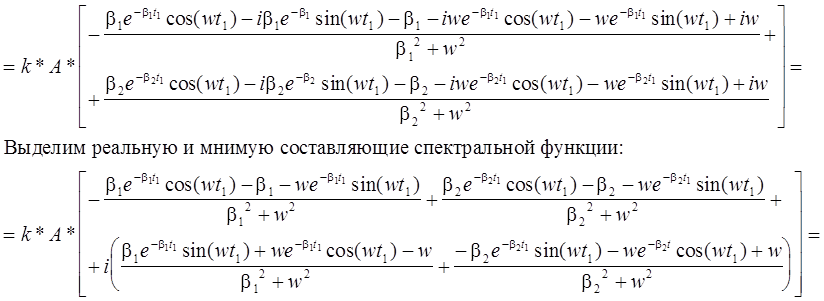
Получили спектральную функцию одиночного импульса стандарта МЭК как сумму реальной  составляющей  и мнимой составляющей спектра:

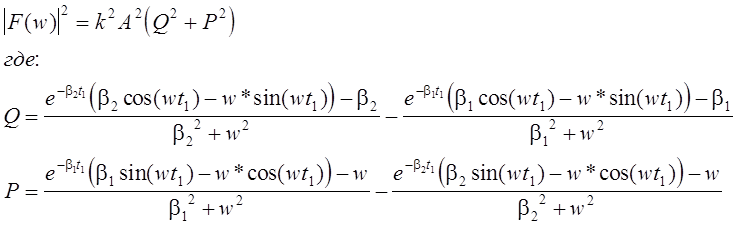
Спектр импульса  в  частотном диапазоне от 0 Гц до 0.3 ГГц представлен на рисунке 3.

Рисунок 3 Расчет спектра одиночного импульса стандарта МЭК с применением MathCAD

Сигналы сложной формы

Согласно  экспертных  оценок   некоторых    специалистов, наибольшую  опасность   для    микроэлектронных    устройств представляют  помехи  от  коммутации  реле  переменного    и постоянного тока, пускателей, двигателей, трансформаторов  и т.д. Помеха от коммутации реле переменного тока (рис. 4) представляет собой пачку коротких импульсов. Поэтому многие национальные и  международные  стандарты предусматривают испытания на пачки помех.

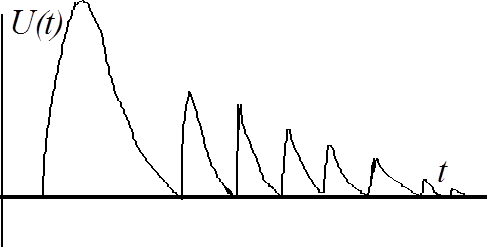
Рис.4. Помеха от коммутации реле переменного тока

Пачка импульсов стандарта МЭК

Рассмoтрим  ,  что  из  себя представляет энергетический спектр "пачки