Другие предметы \ Теория дискретных устройств

Синтез счётчика. Таблица состояний счётчика. Сигналы на информационных входах триггеров. Карта Карно для J1, страница 2


Перейдём от таблиц истинности к картам Карно и запишем минимизированные формулы. Для J1 имеем карту Карно, представленную на рисунке 1.4.1.

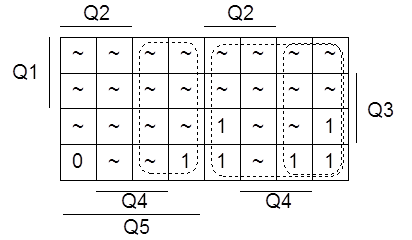
Рисунок 1.4.1 - Карта Карно для J1

Составим формулу по карте и перейдём к базису ИЛИ-НЕ:

Для J2 имеем карту Карно, представленную на рисунке 1.4.2.

 

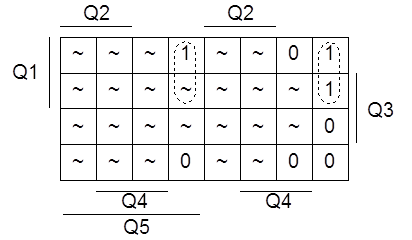
Рисунок 1.4.2 - Карта Карно для J2

Составим формулу по карте и перейдём к базису ИЛИ-НЕ:

Для K2 имеем карту Карно, представленную на рисунке 1.4.3.

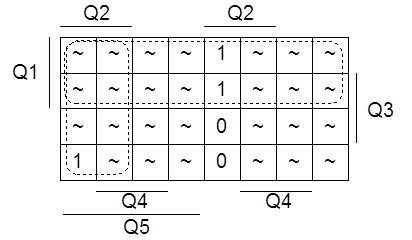
Рисунок 1.4.3 - Карта Карно для K2

Составим формулу по карте и перейдём к базису ИЛИ-НЕ:

Для J3 имеем карту Карно, представленную на рисунке 1.4.4.

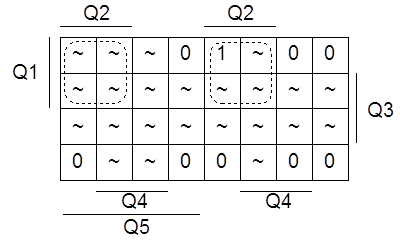
Рисунок 1.4.4 - Карта Карно для J3

Составим формулу по карте и перейдём к базису ИЛИ-НЕ:

Для K3 имеем карту Карно, представленную на рисунке 1.4.5.

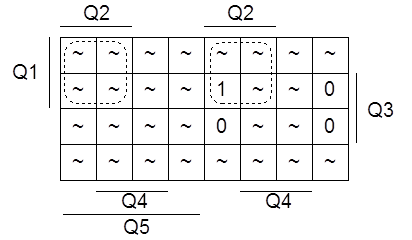
Рисунок 1.4.5 - Карта Карно для K3

Составим формулу по карте и перейдём к базису ИЛИ-НЕ:

Для J4 имеем карту Карно, представленную на рисунке 1.4.6.

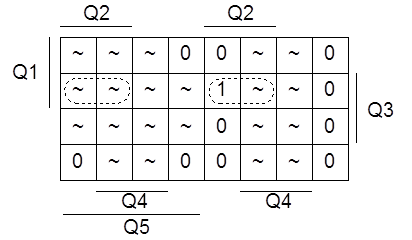
Рисунок 1.4.6 - Карта Карно для J4

Составим формулу по карте и перейдём к базису ИЛИ-НЕ:

Для K4 имеем карту Карно, представленную на рисунке 1.4.7.

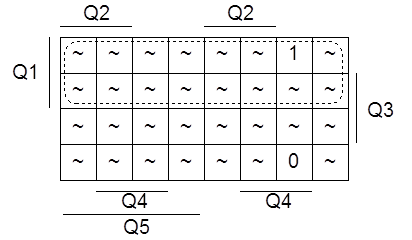
Рисунок 1.4.7 - Карта Карно для K4

Составим формулу по карте:

Для J5 имеем карту Карно, представленную на рисунке 1.4.8.

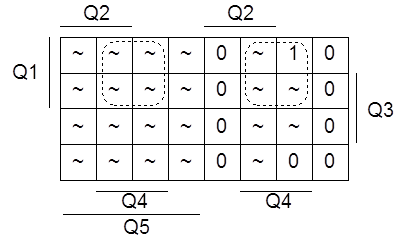
Рисунок 1.4.8 - Карта Карно для J5

Составим формулу по карте и перейдём к базису ИЛИ-НЕ:

Для K5 имеем карту Карно, представленную на рисунке 1.4.9.

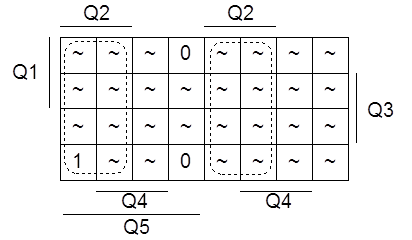
Рисунок 1.4.9 - Карта Карно для K5

Составим формулу по карте:

Воспользуемся минимизацией методом Квайна-Мак-Класки минимум один раз, согласно заданию. Обработаем вход K1 с помощью метода Квайна-Мак-Класки:

Запишем  СДНФ в функции f0, полученной из функции K1 путём задания нулей на всех неопределённых наборах аргументов:

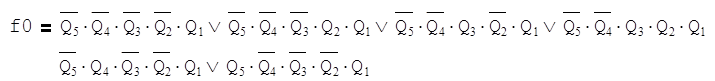
Запишем  СДНФ в функции f1, полученной из функции K1 путём задания единиц на всех неопределённых наборах аргументов:

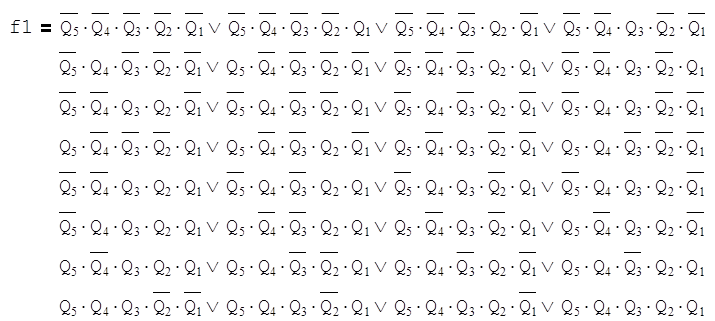
Запишем члены разложения СДНФ  функции f1 по группам в двоичном коде:

0 группа: 00000;

1 группа: 00001;00010;00100;01000;10000;   

2 группа: 11000;01100;00110;00011;10100;01010;00101;10010;

01001;10001;

3 группа: 11100;01110;00111;10110;10011;11010;01101;01011;

10101;11001;

4 группа: 11110;11101;11011;10111;01111;

5 группа: 11111;

I ранг:

0 группа: 0000-;000-0;00-00;0-000;-0000;

1 группа: -1000;-0100;-0010;-0001;1-000;0-100;0-010;0-001;

10-00;01-00;00-10;00-01;100-0;010-0;001-0;000-1;

1000-;0100-;0010-;0001-;

2 группа: -1100;-0110;-0011;-1010;-0101;-1001;1-100;0-110;

0-011;1-010;0-101;1-001;11-00;01-10;00-11;10-10;

01-01;10-01;110-0;011-0;001-1;101-0;010-1;100-1;

1100-;0110-;0011-;1010-;0101-;1001-;

3 группа: -1110;-1101;-1011;-0111;1-110;1-101;1-011;0-111;

01-11;10-11;11-01;11-10;011-1;101-1;110-1;111-0;

0111-;1011-;1101-;1110-;

4 группа: -1111;1-111;11-11;111-1;1111-;

II ранг:

0 группа: --000;0--00;00--0;000--;0-0-0;-0-00;00-0-;0-00-;

-00-0;-000-;

1 группа: 1—-00;10--0;100--;1-0-0;10-0-;1-00-;-1-00;01--0;

010--;-10-0;01-0-;-100-;--100;0-1-0;001--;0-10-;

-01-0;-010-;--010;0--10;00-1-;-0-10;0-01-;-001-;

--001;0--01;00--1;-0-01;0-0-1;0--01;

2 группа: 0--11;01--1;011--;0-1-1;01-1-;0-11-;-0-11;10--1;

101--;-01-1;10-1-;-011-;--011;1-0-1;110--;1-01-;

-10-1;-101-;--101;1--01;11-0-;-1-01;1-10-;-110-;

--110;1--10;11--0;-1-10;1-1-0;1--10;

3 группа: 111--;11--1;--111;1--11;-1-11;1-1-1;11-1-;-11-1;

1-11-;-111-;

III ранг:

0 группа: ---00;--00-;-00--;00---;0-0--;-0-0-;--0-0;0--0-;

-0--0;0---0;

1 группа: ---10;--1-0;-1--0;1---0;0---1;0--1-;0-1--;01---;

01---;-10--;-1-0-;-1--0;0-1--;-01--;--10-;--1-0;

-0-1-;--01-;---10;

2 группа: 11---;-11--;--11-;---11;1-1--;-1-1-;--1-1;1--1-;

-1--1;1---1;

IV ранг:

0 группа: 0----;-0---;--0--;---0-;----0;

1 группа: 1----;-1---;--1--;---1-;----1;

V ранг:       -----.

Составим импликантную таблицу (Таблица 1.4.2):

Таблица 1.4.2 – Импликантная таблица (для К1 - счётчика):

00001

00011

00101

00111

01001

10001

-----

V

V

V

V

V

V

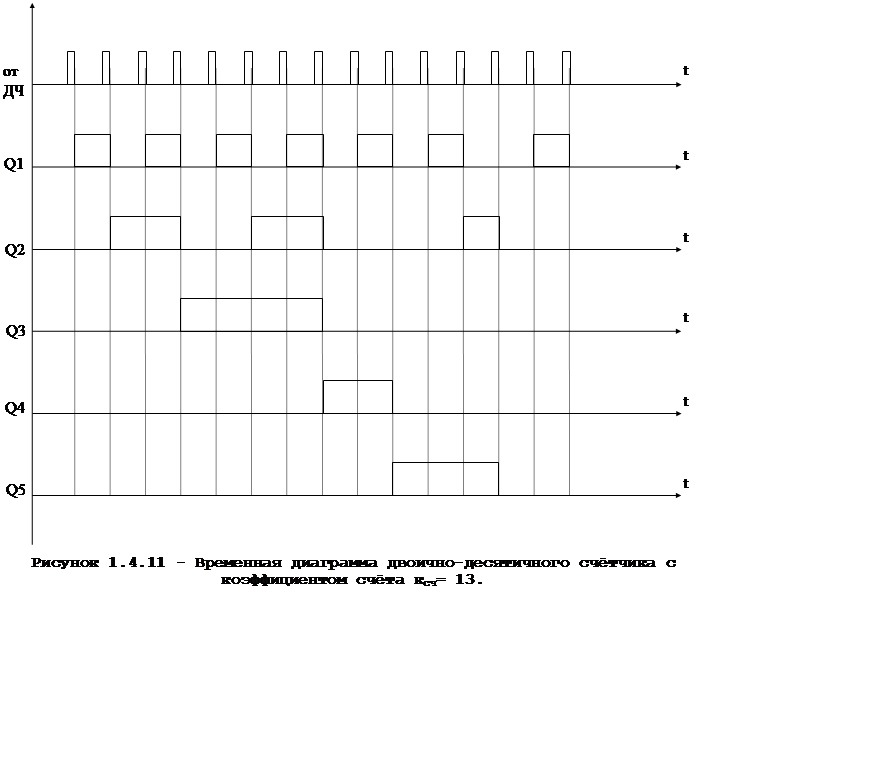
По полученным формулам осуществляем соединение триггеров. На рисунке 1.4.10 приведена схема двоично-десятичного счётчика с коэффициентом счёта ксч= 13. Временная диаграмма, поясняющая процесс функционирования счетчика, приведена на рисунке 1.4.11.

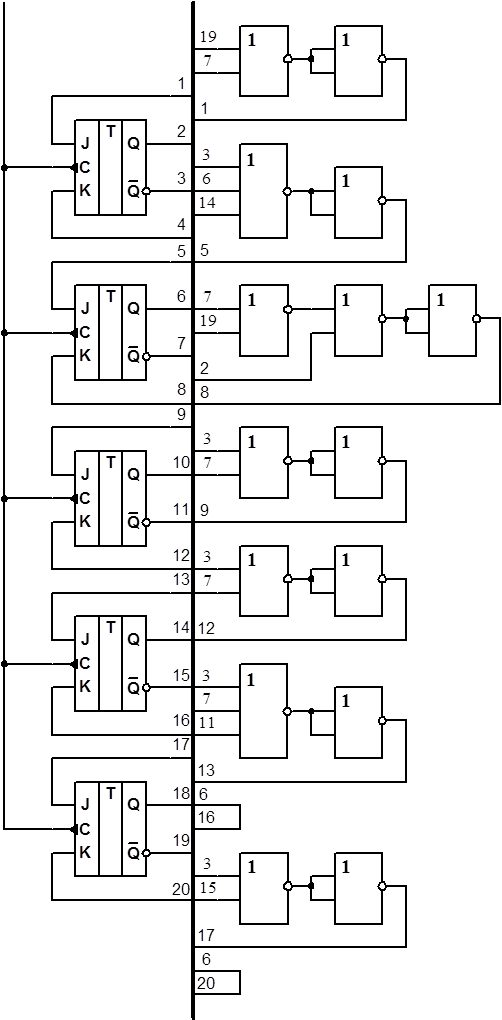
Рисунок 1.4.10 – Схема двоично-десятичного счётчика

 

Скачать файл