Синтез асинхронных конечных автоматов. Изучение и применение на практическом примере метода синтеза асинхронного конечного автомата с помощью кодирования состояний по столбцам таблицы переходов, страница 3

Для того чтобы АКА выполнил заданный алгоритм работы, критические состязания элементов памяти в нем должны быть исключены.

2.  МЕТОД КОДИРОВАНИЯ СОСТЯЗАНИЙ ПО СТОЛБЦАМ ТП.

Рассмотрим универсальный метод синтеза АКА с помощью кодирования состояний по столбцам ТП. Данный метод не требует анализа всех возможных случаев состязаний и обеспечивает устойчивость работы АКА при выбранном варианте кодирования. В качестве примера используем ТП (табл. 5).

Будем называть l - классом столбца а_j множество состояний, содержащее устойчивое состояние и все неустойчивые состояния, из которых задан переход в данное устойчивое состояние.

Столбец а₁ содержит 3 l - класса: l₁={ 1,6,7 }, l₂={ 2,3 }, l₃={ 4,5 }.

Столбец а₂ содержит четыре l-класса: l₅={ 1,3 }, l₆={ 2,4 },                   l₇={ 5,6 },l₈={ 7 }.

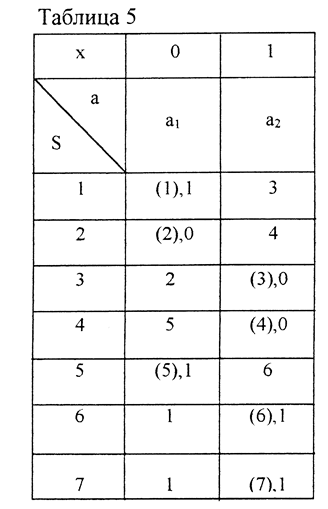Рассмотрим переходы схемы по столбцу а₁. Имеем переход из состояний 6 и 7 в состояние 1. Эти переходы осуществляются внутри класса l₁; переход из 3 в 2 внутри l₂; из 4 в 5 внутри l₃. Критические состязания возникают, если схема вместо одного устойчивого состояния ложно перейдет в другое устойчивое состояние, т. е., если из одного класса l схема ложно перейдет в другой класс l.

Необходимо исключить такие ложные переходы между l - классами. Для этой цели в столбце а_j необходимо выделить для кодирования состязаний, принадлежащих l - классам, специальные внутренние переменные, которые имеют следующие свойства.

Свойство 1. Для состязаний, принадлежащих одному l - классу, они имеют одинаковое значение.

Свойство 2. Для состязаний, принадлежащих разным l - классам, они имеют разное значение.

Свойство 3. При любом переходе внутри столбца а_j они не меняют своего значения.

Свойство 4. Поведение АКА в столбце а_j зависит только от этих переменных.

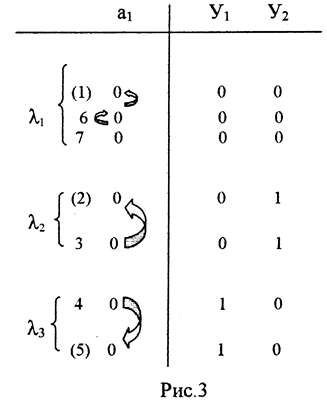На рис. 3 представлены l - классы для столбца а₁ и выделены внутренние переменные У₁ и У₂, которые, будем считать, обладают свойствами 1-4.

Предположим, что в схеме осуществляется переход из состояния 5 внутри

класса l₃. Во время этого перехода значение внутренних переменных У₁ и У₂ не меняется (свойство 3), так как и для состояния 4, и для состояния 5 У₁=1  У₂=0 (свойство 1). Нахождение схемы в состояниях, принадлежащих классу l₃ можно определить конъюнкцией а₁         (свойство 4).

Для других состояний l - классов этого же столбца имеем: для l₁ -  для l₂ - . Очевидно, что все конъюнкции отличаются хотя бы одним значением переменной У (свойство 2). Будем говорить, что l - классы по столбцу а₁ разделены внутренними переменными У₁ и У₂ (т. е. отличают их друг от друга). Эти переменные будем называть разделяющими.

Таким образом можно сделать вывод, что при кодировании состояний, принадлежащих l - классам столбца а_j разделяющими переменными, обладающими свойствами 1-4, исключаются ложные переходы между l - классами, а следовательно и критические состязания.

Рассмотрим способ кодирования строк ТП, который обеспечивает выполнение этого условия,

Будем обозначать через n_j – общее число устойчивых состояний или число l - классов столбца а_j. Для разделения l - классов столбца а_j необходимо выделять N=] log₂ n j [ разделяющих переменных.

Для примера имеем:

N₁  =  ] log₂ n₁ [  =  ] log₂ 3 [  =  2.

N₂  =  ] log₂ n₂ [  =  ] log₂ 4 [  =  2.

Таким образом, для разделения l - классов по столбцу а₁ требуется две переменные у₁ и у₂, а по столбцу а₂ также две переменные у₃ и у₄, классов столбца а₂ разделяющими переменными У₃ и У₄. На рис.4 приведен один из вариантов кодирования состояний l - классов.

Общее кодовое слово i-ой строки ТП образуется совокупность значений всех переменных по всем столбцам i-ой строки.