Каждый разряд десятичного числа представляет собой двоичный счётчик и затем с помощью специальных схемных решений эти двоичные счётчики соединяются между собой.
1) Определим число триггеров путём перевода ксч, заданного в десятичной форме в двоичную систему счисления:
2к-1![]() 9
9![]() 2к
2к
Отсюда, к=4, т.е. на младший разряд необходимо 4 триггера, а на старший 1 триггер;
2) Тип триггера : D- триггер;
3) Составим таблицу 2 предыдущего и последующего состояния счётчика, где расписываем все состояния входов:
Таблица 2
|
№ |
Предыдущее состояние |
Последующее состояние |
Информацион- ные входы |
||||||||||||
|
Qn4 |
Qn3 |
Qn2 |
Qn1 |
Qn+14 |
Qn+13 |
Qn+12 |
Qn+11 |
D4 |
D3 |
D2 |
D1 |
||||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|||
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|||
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|||
|
3 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|||
|
4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|||
|
5 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|||
|
6 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|||
|
7 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|||
|
8 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|||
|
9 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||
Обработаем вход D4 с помощью метода Квайна:
1) Запишем СДНФ в функции d0, полученной из функции D4 путём задания нулей на всех неопределённых наборах аргументов:
d0=![]()
2) Запишем СДНФ в функции d1, полученной из функции D4 путём задания единиц на всех неопределённых наборах аргументов и произведём попарное склеивание:
d1=![]()
![]()
![]()
![]()
![]()
3) Минимизируем функцию d1 и приведём её к упрощённой форме:
Составим импликантную таблицу(òàáëèöó 3):
Таблица 3
|
|
|
|
|
||
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|
|
d1=![]()
4) Составим импликантную таблицу из всех членов функции d0 и простых конъюнкций, упрощенной d1(таблица 4):
Таблица 4
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|||
|
|
5) Запишем результат минимизации:
D4=![]() ;
;
Для остальных входов используем минимизацию методом карт Карно:
Перейдём от таблиц истинности к картам Карно и запишем минимизированные формулы:
D1:
Q2
|
Q1 |
0 |
0 |
0 |
|||
|
0 |
0 |
|||||
|
1 |
1 |
Q3 |
||||
|
1 |
1 |
1 |
||||
Q4
D1=![]() ;
;
D2:
Q2
|
Q1 |
0 |
0 |
1 |
|||
|
0 |
1 |
|||||
|
1 |
0 |
Q3 |
||||
|
1 |
0 |
0 |
||||
Q4
Перейдём к базису И-НЕ:
D2=![]()
![]()
![]() ;
;
D3:
Q2
|
Q1 |
1 |
0 |
0 |
|||
|
0 |
1 |
|||||
|
1 |
1 |
Q3 |
||||
|
0 |
0 |
0 |
||||
Q4
Перейдём к базису И-НЕ:
D3=![]()
![]()
![]() ;
;
На рисунке 1.3 приведена схема двоично-десятичного счётчика с коэффициентом счёта ксч= 12.
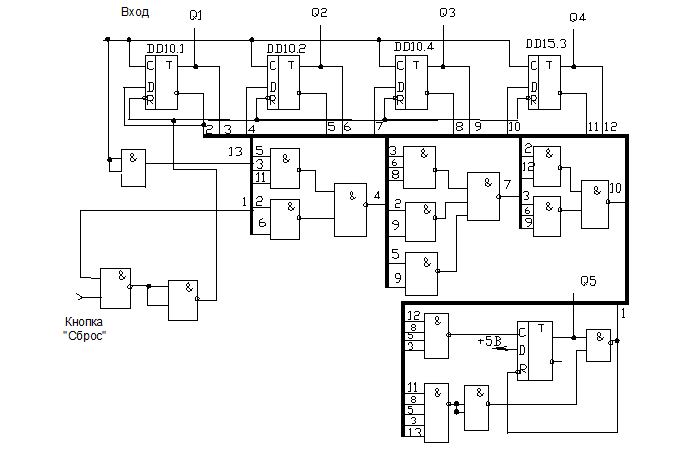
Рисунок 1.3 Двоично-десятичный счётчик с ксч=12
Дешифратор преобразует двоичные числа в десятичные.
Так как в данном курсовом проекте дешифратор следует после счетчика, то он преобразует двоичные числа представленные в коде 8421 в десятичные
1) Учитывая, что счётчик двоично-десятичный составим таблицу истинности (таблица 5):
Таблица 5
|
Десятичное число |
x4 |
x3 |
x2 |
x1 |
|
|
0 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
1 |
|
|
2 |
0 |
0 |
1 |
0 |
|
|
3 |
0 |
0 |
1 |
1 |
|
|
4 |
0 |
1 |
0 |
0 |
|
|
5 |
0 |
1 |
0 |
1 |
|
|
6 |
0 |
1 |
1 |
0 |
|
|
7 |
0 |
1 |
1 |
1 |
|
|
8 |
1 |
0 |
0 |
0 |
|
|
9 |
1 |
0 |
0 |
1 |
По таблице 5 можем составить независимые формулы для каждого выхода (СДНФ):
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
На рисунке 1.4 приведена схема дешифратора.
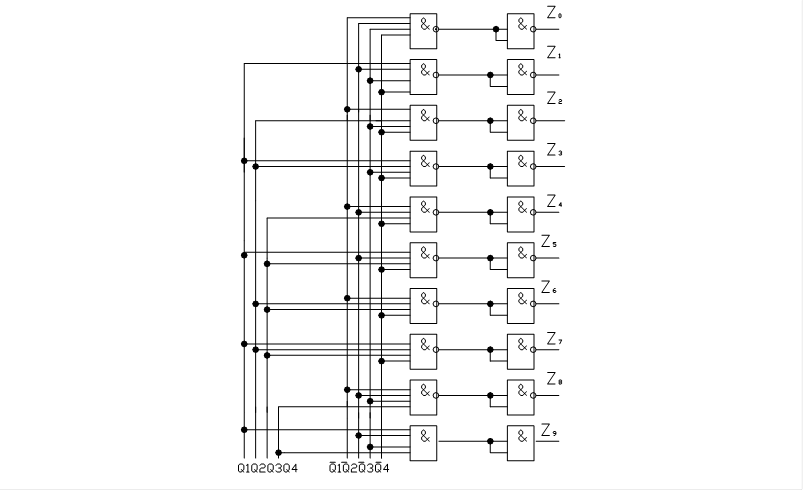
Рисунок 1.4 Схема дешифратора
Схему с одним выходом Q, k, управляющими входами А1,А2,...,Ак, n=2k-1, информационными входами D0,D1,...,Dn называют мультиплексором (коммутатором).
Набор переменных, поступающих на управляющие входы, задаёт двоичное число Ni вида x1,x2,x3....xk. Выходная переменная мультиплексора Q повторяет переменную информационного входа DNi с номером Ni, задаваемым двоичным кодом на управляющих входах [ 3 ]. В данном курсовом проекте мультиплексор имеет одиннадцать информационных входа. Следовательно, число адресных входов равно четырём.
Функционирование мультиплексора определяется таблицей 6.
Таблица 6
|
Адресные входы |
Выход |
||||||
|
А1 |
А2 |
А3 |
А4 |
Q |
|||
|
0 |
0 |
0 |
0 |
D0 |
|||
|
1 |
0 |
0 |
0 |
D1 |
|||
|
0 |
1 |
0 |
0 |
D2 |
|||
|
1 |
1 |
0 |
0 |
D3 |
|||
|
0 |
0 |
1 |
0 |
D4 |
|||
|
1 |
0 |
1 |
0 |
D5 |
|||
|
0 |
1 |
1 |
0 |
D6 |
|||
|
1 |
1 |
1 |
0 |
D7 |
|||
|
0 |
0 |
0 |
1 |
D8 |
|||
|
1 |
0 |
0 |
1 |
D9 |
|||
|
0 |
1 |
0 |
1 |
D10 |
|||
По таблице можно составить логическое выражение:
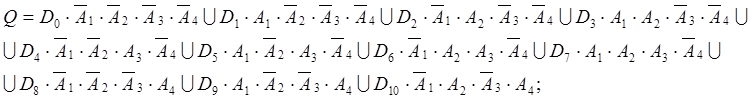
Преобразуем в базис И-НЕ.
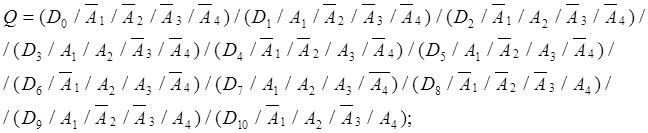
На рисунке 1.5 приведена схема мультиплексора.
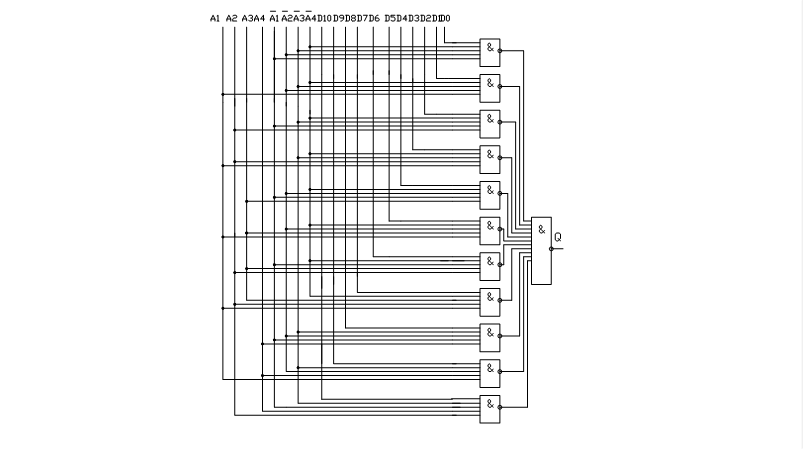
Рисунок 1.5 Схема мультиплексора
Регистром называется устройство, выполняющее функции приёма, хранения, преобразования и передачи информации. Информация в регистрах хранится в виде числа (слова), представляющих собой комбинацию символов 0 и 1. Каждому разряду числа, записанному в регистр, соответствует разряд регистра.
В сдвигающих регистрах запись кода осуществляется путём последовательного сдвига кода тактовыми импульсами, начиная с младшего или старшего разрядов.
В данном курсовом проекте синтезируем одиннадцати разрядный регистр сдвига, выполненный на D- триггерах. Информацию начинаем записывать в старший разряд регистра.
На рисунке 1.6 приведена схема регистра сдвига, выполненного на D- триггерах.
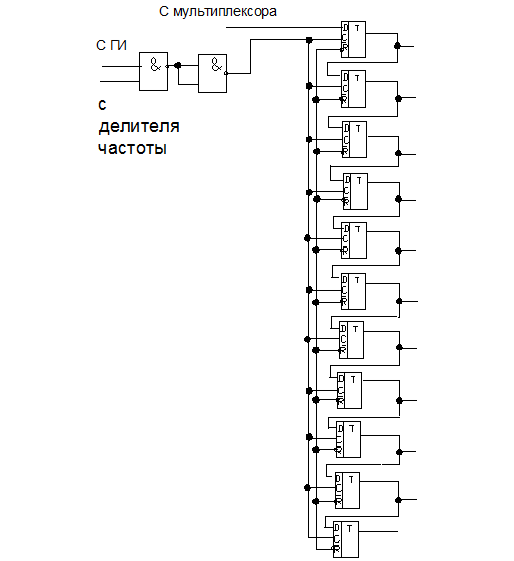
Рисунок 1.6 Схема регистра сдвига
На принципиальной схеме дискретного устройства, выполненного на логических элементах И-НЕ и D- триггерах, используемых в качестве элементов памяти, показана реализация функциональных блоков этого устройства:
n генератора тактовых импульсов (ГИ);
n делителя частоты;
n двоично-десятичного счётчика;
n дешифратора;
n мультиплексора;
n регистра сдвига;
Так как в качестве элементной базы применяются микросхемы серии К155, то для их запитки используется блок питания с выходным напряжением U=+5 В.
Первым функциональным блоком в схеме является генератор тактовых импульсов, представляющий собой кварцевый генератор, вырабатывающий тактовые импульсы с частотой f=100 кГц.
С выхода генератора импульсы поступают на вход делителя частоты на одиннадцать, который необходим для того, чтобы импульсы на информационные входы мультиплексора поступали в 11 раз медленнее чем на адресные. При этом информационные входы по очереди подключаются к выходу мультиплексора. Одновременно делитель частоты выполняет функции двоичного счётчика на 4 триггерах, имеющего коэффициент счёта равный одиннадцати для подачи сигналов на управляющие входы мультиплексора.
С выхода делителя частоты импульсы поступают на тактовый вход двоично-десятичного счётчика с коэффициентом счёта ксч=12. С выходов младшего разряда двоично-десятичного счётчика информация
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.