Разработка интерфейса распознающей системы. Средства для разработки интуитивно понятного интерфейса. Алгоритмические методы задания функции

Кафедра «МТ и УС»

ОТЧЁТ

По лабораторным работам

по дисциплине

«Техническая кибернетика»

Проверила доцент

Выполнил студент группы ЭМ-41

1999

Лабораторная работа №1 Разработка интерфейса распознающей системы

Цель работы: разработать удобный и интуитивно понятный интерфейс для программы распознавания образов. Предусмотреть выбор метода распознавания.

Ход работы:

Средства для разработки интуитивно понятного интерфейса предоставляет Borland C++ Builder 3.0.

Информация об авторе:

Лабораторная работа №2 Алгоритмические методы задания функции

Цель работы: изучить методы распознавания образов, реализовать программно методы «Ближайшего соседа» и «К - ближайших представителей».

Ход работы.

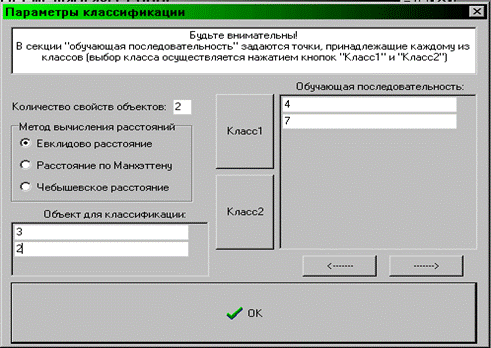
Выбор метода распознавания:

Правило ближайшего соседа является наиболее простым методом классификации объектов. Суть метода заключается в следующем: ищется ближайшая к распознаваемому объекту точка из обучающей последовательности; объект Zi относят к классу, к которому принадлежит эта  точка. Таким образом, в основе решения этой задачи лежит понятие расстояния между объектами - точками признакового пространства. В зависимости от свойств объектов и исследуемого процесса могут быть использованы различные формализованные определения  расстояния между точками.

Наиболее распространенными являются следующие определения:

r₁ – евклидово расстояние

   ,                                           ( 1 )

r₂ –расстояние  по Манхэттену

      ,                                        ( 2 )

r₃  - Чебышевское расстояние

                                                    ( 3 )

Здесь через    обозначена  i-я  составляющая j-го вектора.

В работе также используется определение расстояния в смысле Камберра:

                                                        ( 4 )

В случае некорректного ввода программа предупреждает пользователя:

Результаты распознавания по методу ближайшего соседа:

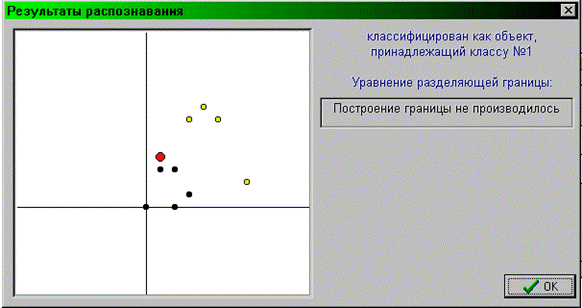
Обобщением метода ближайшего соседа является метод  К- представителей, согласно которому объект относят к тому классу, к которому принадлежит большинство из к ближайших к нему объектов обучающей последовательности.

Для того, чтобы избежать неопределенности, удобнее к выбирать нечетным. Итак, К - произвольное нечетное число, величина которого выбирается исходя из требований точности классификации с одной стороны и уменьшения машинных расчетов с другой. При больших К вероятность ошибки 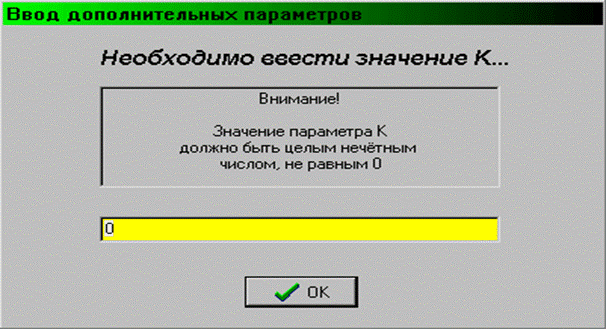классификации мала, но возрастают затраты машинного времени.

В случае некорректного ввода программа предупреждает пользователя:

К недостаткам метода следует отнести необходимость хранения в памяти всей обучающей последовательности, вычисления при классификации расстояний между всеми точками обучающей последовательности и классифицируемым объектом. Этот метод желательно применять при небольших объемах обучающих и распознаваемых выборок.

Вывод: метод К – ближайших представителей является более точным по сравнению с методом ближайшего соседа, однако он обладает рядом недостатков, среди которых и сложности при программировании. На рассмотренных примерах в процессе тестирования программы расхождений в классификациях, данных обоими методами не выявлено.

Лабораторная работа №3 Метод эталона

Цель работы: Изучить метод эталона, выявить достоинства и недостатки этого метода, написать блок к программе, осуществляющий классификацию объектов этим методом. Реализовать построение разделяющей границы в методе эталона.

Метод эталона в своей простейшей постановке может рассматриваться как частный случай метода К- ближайших представителей, если в качестве К- ближайших точек рассматриваются все точки обучающей последовательности. Возникает задача определения расстояния между точкой и классом. Расстоянием между точкой и классом считается расстояние между этой точкой и эталоном класса - его центром тяжести.

Координаты эталона рассчитываются по формуле

                                  ( 1 )

где Kj- число объектов обучающей последовательности j –го класса,  X_i –i-я координата эталона, X_i^j – i-я координата  l-той точки j-го класса.

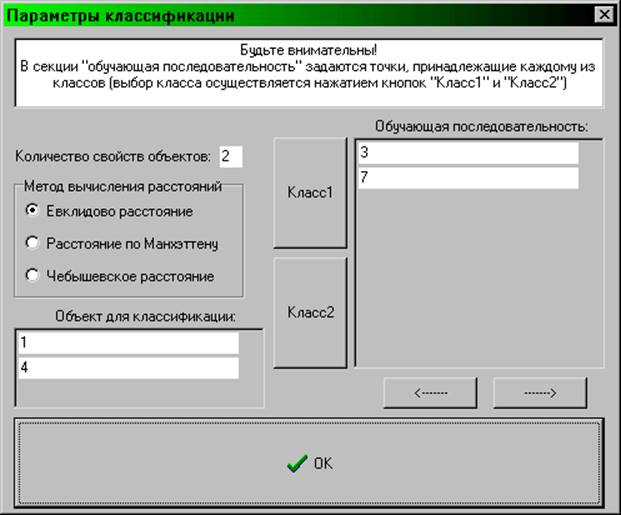Метод эталона позволяет резко сократить объемы хранимой информации объемы вычислительной работы при распознавании объектов за счет построения разделяющей границы между классами и формировании на ее основе аналитического выражения для решающего правила.

Алгоритм построения разделяющей границы между классами и методом эталона заключается в следующем:

1. Для каждого класса по формуле (1) рассчитывается эталон - наиболее типичный представитель класса.

2. Все признаковое пространство делится на две части гиперповерхностью, все точки которой одинаково отстоят от эталонов.

   Распознавание объектов можно производить без построения разделяющей границы на основании сравнения расстояний от исследуемой точки до эталона. В этом случае в памяти необходимо хранить только эталоны и вычислить всего два расстояния.

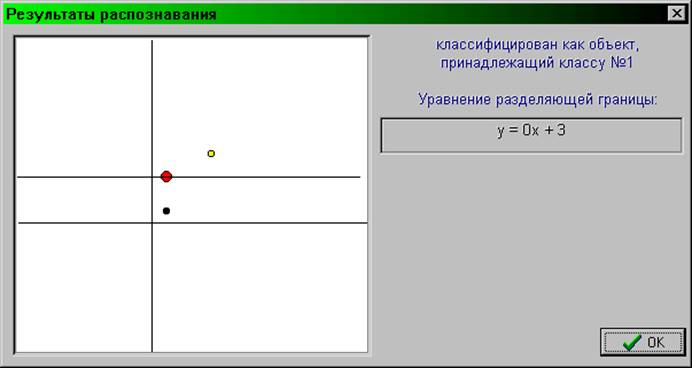Вывод: Метод разделяющей границы позволяет значительно сократить