Исследование детерминированных процессов. Процессы во временной области. Гармонический сигнал, амплитуда, страница 2

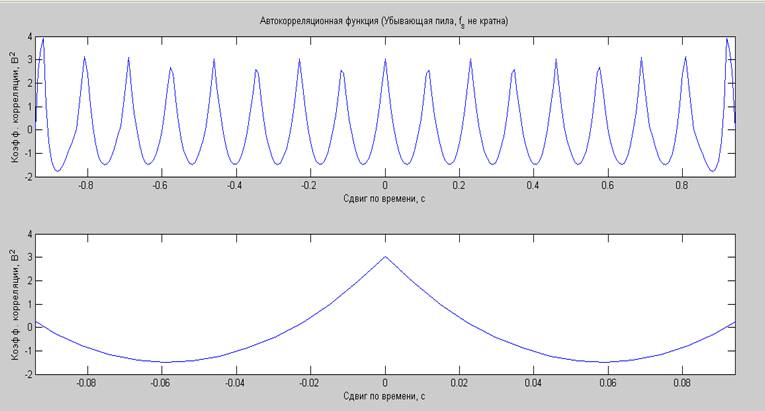
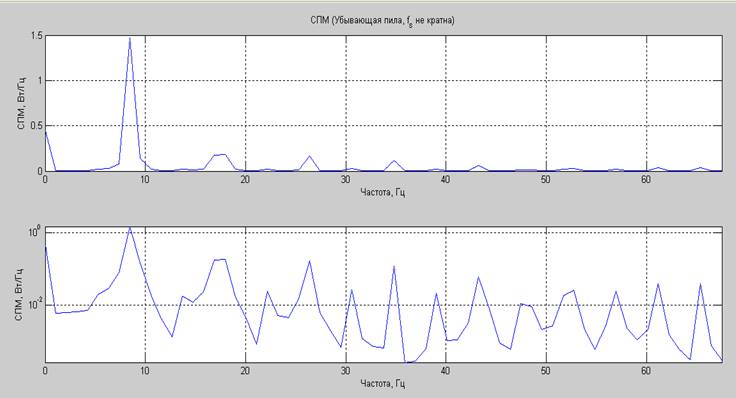
Математическое ожидание сгенерированного процесса: 0.6824 В.

Дисперсия сгенерированного процесса: 3.0499 В².

Суммарная мощность (по постоянной и переменной составляющим) сгенерированного процесса: 3.5156 Вт.

Средняя мощность, вычисленная по автокорреляционной функции, плюс мощность постоянной составляющей: 3.4918 Вт.

Средняя мощность, вычисленная по СПМ: 3.4918Вт.

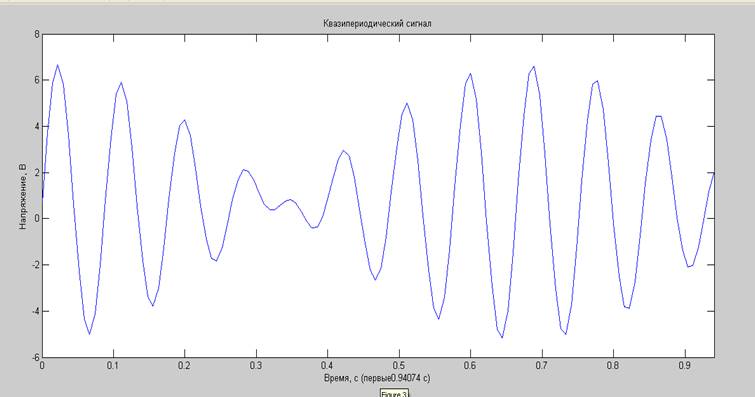
11) Квазипериодический сигнал (биения), амплитуды 3 В, постоянная составляющая 0.7 В, частоты 10.5469 Гц и *10.5469 Гц.

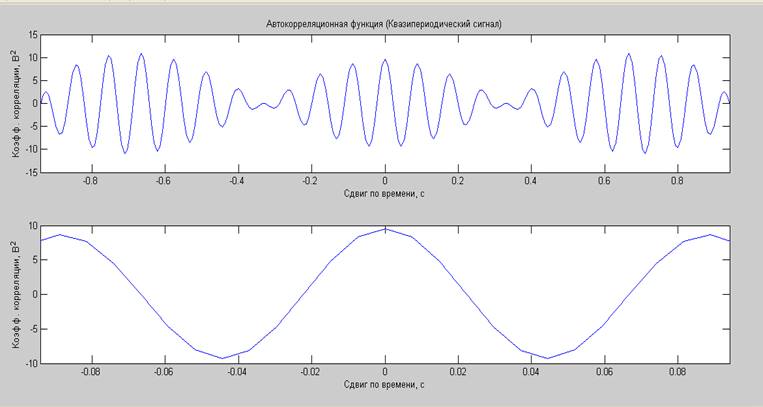
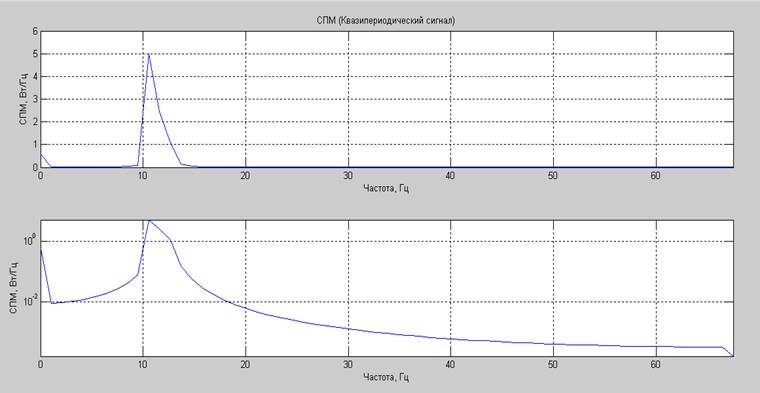
Математическое ожидание сгенерированного процесса: 0.7672В.

Дисперсия сгенерированного процесса: 9.6417В².

Суммарная мощность (по постоянной и переменной составляющим) сгенерированного процесса: 10.2303Вт.

Средняя мощность, вычисленная по автокорреляционной функции, плюс мощность постоянной составляющей: 10.1550Вт.

Средняя мощность, вычисленная по СПМ: 10.1550Вт.

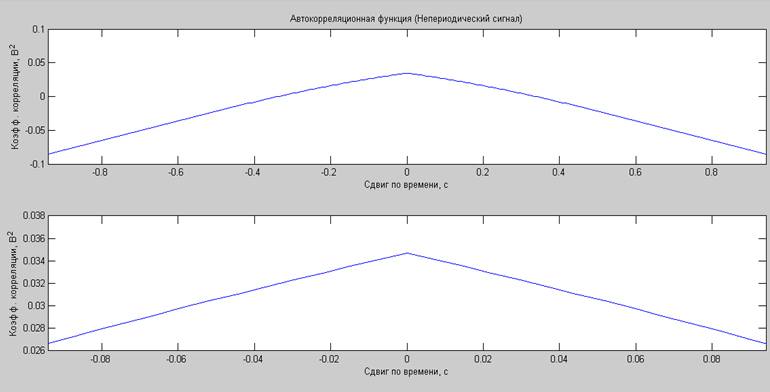
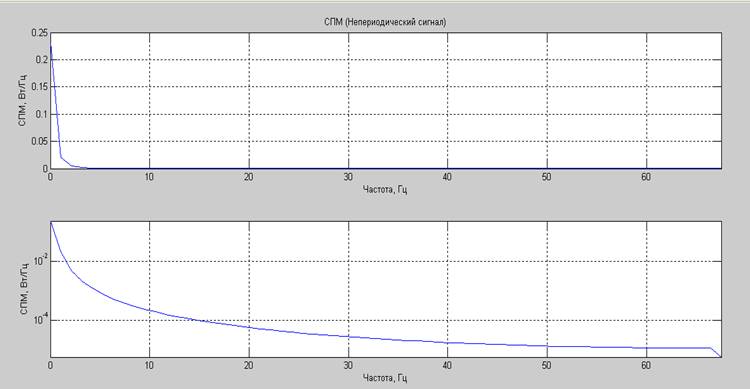
12) Непериодический сигнал, амплитуда 0.7, постоянная составляющая 0.7 В

Математическое ожидание сгенерированного процесса: 0.4927 В.

Дисперсия сгенерированного процесса:  0.0350В².

Суммарная мощность (по постоянной и переменной составляющим) сгенерированного процесса: 0.2777Вт.

Средняя мощность, вычисленная по автокорреляционной функции, плюс мощность постоянной составляющей: 0.2774Вт.

Средняя мощность, вычисленная по СПМ: 0.2774Вт.

Выводы: Спектры периодических детерминированных сигналов, имеющих частоту кратную разрешению по частоте, имеют четкие пики гармоник в спектре, а не кратную соответственно размытые. Количество отсчётов взято равным степени числа два для быстрого вычисления ДПФ. Для сигналов мы выбираем наименьшую частоту в предложенном диапазоне, удовлетворяющую условию кратности/не кратности Δf и теореме Котельникова. Цель такого выбора в том, чтобы до частоты Найквиста в спектре поместилось больше гармоник. Квазипериодический сигнал является таковым весьма условно, так как в компьютере ограничена разрядная сетка и представление иррациональных чисел невозможно, все числа в компьютере рациональные. Оценка автокорреляционной функции была получена несмещённой.

Код MatLab:

clc;

clear all;

%Входные данные

fd = 135; %частота дискретизации

N = 2^7; %число отсчетов

df = fd/N; %частотное разрешение

t = (0:N - 1)/fd; %время

fs = df*10; %частота сигнала (кратна разрешению по частоте)

fsNotKr = df*8.25; %частота сигнала не кратна разреш.

amplit = 3; %аплитуда сигнала

post_sost = 0.7; %постоянная состовляющая

%Выбор зависимости и выбор выводимых параметров

zavisimostN = 12;

ifFormaSign = 0;

ifCorreliats = 0;

ifSpectr = 1;

%Описание заданных процесов

names{1} = 'Гармонический сигнал';

sig(1, :) = amplit*sin(2*pi*fs*t) + post_sost;

names{8} = 'Гармонический сигнал, f_s не кратна ';

sig(8, :) = amplit*sin(2*pi*fsNotKr*t) + post_sost;

names{2} = 'Меандр';

sig(2, :) = amplit*square(2*pi*fs*t) + post_sost;

names{9} = 'Меандр, f_s не кратна ';

sig(9, :) = amplit*square(2*pi*fsNotKr*t) + post_sost;

names{3} = 'Равнобокая пила';

sig(3, :) = amplit*sawtooth(2*pi*fs*t, 0.5) + post_sost;

names{10} = 'Равнобокая пила, f_s не кратна ';

sig(10, :) = amplit*sawtooth(2*pi*fsNotKr*t, 0.5) + post_sost;

names{4} = 'Возрастающая пила';

sig(4, :) = amplit*sawtooth(2*pi*fs*t, 1) + post_sost;

names{11} = 'Возрастающая пила, f_s не кратна ';

sig(11, :) = amplit*sawtooth(2*pi*fsNotKr*t, 1) + post_sost;

names{5} = 'Убывающая пила';

sig(5, :) = amplit*sawtooth(2*pi*fs*t, 0) + post_sost;

names{12} = 'Убывающая пила, f_s не кратна ';

sig(12, :) = amplit*sawtooth(2*pi*fsNotKr*t, 0) + post_sost;

names{6} = 'Квазипериодический сигнал';

sig(6, :) = amplit*sin(2*pi*fs*t) + amplit*sin(2*pi*fs*sqrt(1.3)*t) + post_sost;

names{7} = 'Непериодический сигнал';

sig(7, :) = -0.7*t.^2 + post_sost;

y = sig(zavisimostN, :);

if zavisimostN > 7

fs = fsNotKr;

end;

%Вывод исходного процесса

if ifFormaSign == 1

figure;

plot(t, y);

title(names{zavisimostN});

xlabel(strcat('Время, с (первые ', num2str(10/fs - 1/fd), ' c)'));

ylabel('Напряжение, В');

xlim([0 10/fs - 1/fd]);

end;

%Статистические хар-ки

meanSig = mean(y)

covSig = cov(y)

powerSig = meanSig.^2 + covSig

%Корреляционные хар-ки

if ifCorreliats == 1

[corrSig,lags] = xcorr(y - meanSig, 'unbiased');

figure;

subplot(2, 1, 1);

plot(lags/fd, corrSig);

title(strcat('Автокорреляционная функция (', names{zavisimostN}, ')'));

xlabel('Сдвиг по времени, с');

ylabel('Коэфф. корреляции, В^{ 2}');

xlim([lags(1) lags(end)]/fd);

subplot(2, 1, 2);

plot(lags/fd, corrSig);

xlabel('Сдвиг по времени, с');

ylabel('Коэфф. корреляции, В^{ 2}');

xlim([lags(1) lags(end)]/fd/10);

powerCorrSig = corrSig(N) + meanSig^2

end;

%Спектральные хар-ки

if ifSpectr == 1

spdSig = fft(y);

spdSig = 2*spdSig.*conj(spdSig)/(N*fd);

spdSig(1) = spdSig(1)/2;

spdSig = spdSig(1:N/2 + 1);

spdSig(end) = spdSig(end)/2;

f = fd/N*(0:(N/2));

figure;

subplot(2, 1, 1);

plot(f, spdSig);

title(strcat('СПМ (', names{zavisimostN}, ')'));

grid on;

xlabel('Частота, Гц');

ylabel('СПМ, Вт/Гц');

xlim([f(1) f(end)]);

subplot(2, 1, 2);

spdSigTemp = spdSig;

spdSigTemp(spdSigTemp == 0) = 1e-40;

semilogy(f, spdSigTemp);

grid on;

xlabel('Частота, Гц');

ylabel('СПМ, Вт/Гц');

xlim([f(1) f(end)]);

ylim([min(spdSigTemp) max(spdSigTemp)]);

powerFtSig = sum(spdSig, 2)/N*fd

end;