Функции. Передача в функцию параметров стандартных типов. Передача имени функции в качестве параметра

ЛАБОРАТОРНАЯ РАБОТА  № 3. Функции

3.1. Передача в функцию параметров стандартных типов

Все необходимые данные для функций должны передаваться им в качестве параметров. Использование глобальных переменных в функциях не допускается.

1. Выполнить соответствующий вариант задания 2.1 лабораторной работы №2, оформив его с использованием функции.
2. Выполнить соответствующий вариант задания 2.3 лабораторной работы №2, оформив в виде функции вычисление значения многочлена по схеме Горнера в точке.
3. Выполнить соответствующий вариант задания 2.6 лабораторной работы №2, оформив в виде функции вычисление ряда Тейлора в точке.

3.2. Перегрузка и шаблоны функций

1. Выполнить соответствующий вариант задания 1.2.1 лабораторной работы №1, реализовав его через механизм функций и обеспечив их перегрузку для типов int, float, double. Кроме того, создать шаблон семейства этих функций.

2. Выполнить соответствующий вариант задания 2.3. лабораторной работы №1, реализовав его через механизм функций и обеспечив их перегрузку для типов int, float, double. Кроме того, создать шаблон семейства этих функций.

3.3. Передача имени функции в качестве параметра

Вариант 1.

a) Вычислить интеграл 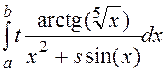 методом правых прямоугольников, воспользовавшись критерием двойного пересчета с точностью e = 10^–6  при  a = 0,1; b = 1,2; s = 0,1; t = 1,4. Вычисление значения функции в точке и вычисление интеграла оформить в виде функции.

b) Для заданных функций f(x) вычислить корень уравнения  на отрезке [a; b] с точностью e = 10^–6, используя  метод половинного деления и выполнив предварительно отделение корней:

1. f(x) = x² - 3;  a = 1;  b = 3;

2*. f(x) = ;  a = 0;  b = 1,5;  sÎ[0,1; 1,3];  Ds = 0,3.

Вычисление корня уравнения оформить в виде функции с функциональным параметром, параметры a, b, e, s – в виде  аргументов по умолчанию. Результат представить в виде таблицы (s – значение параметра, х – вычисленный корень уравнения, f(x) – значение функции в найденной точке х, k_iter – количество итераций цикла для получения корня с заданной точностью).

Вариант 2.

a) Вычислить интеграл 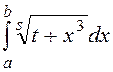 методом правых прямоугольников, воспользовавшись критерием двойного пересчета с точностью e = 10^–6  при  a = 0,81; b = 1,762; s = 1,5; t = 1. Вычисление значения функции в точке и вычисление интеграла оформить в виде функции.

b) Для заданных функций f(x) вычислить корень уравнения  на отрезке [a; b] с точностью e = 10^–6, используя  метод касательных и выполнив предварительно отделение корней:

  1. f(x) = x³ - 3;  a = 1;  b = 4;

2*. f(x) = ;  a = 0;  b = 4,5;  sÎ[0,5; 2];  Ds = 0,5.

Вычисление корня уравнения оформить в виде функции с функциональным параметром, параметры a, b, e, s – в виде  аргументов по умолчанию. Результат представить в виде таблицы (s – значение параметра, х – вычисленный корень уравнения, f(x) – значение функции в найденной точке х, k_iter – количество итераций цикла для получения корня с заданной точностью).

Вариант 3.

a) Вычислить интеграл 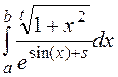 методом правых прямоугольников, воспользовавшись критерием двойного пересчета с точностью e = 10^–6  при  a = – 1; b = 1; s = 2; t = 3. Вычисление значения функции в точке и вычисление интеграла оформить в виде функции.

b)  Для заданных функций f(x) вычислить корень уравнения  на отрезке [a; b] с точностью e = 10^–6, используя  метод хорд и выполнив предварительно отделение корней:

1. f(x) = (x-1)² - 3 ; a = 1; b = 4;

2*. f(x) = ;   a = 0;   b = 2;  sÎ[0,3; 0,7];   Ds = 0,1.

Вычисление корня уравнения оформить в виде функции с функциональным параметром, параметры a, b, e, s – в виде  аргументов по умолчанию. Результат представить в виде таблицы (s – значение параметра, х – вычисленный корень уравнения, f(x) – значение функции в найденной точке х, k_iter – количество итераций цикла для получения корня с заданной точностью).

Вариант 4.

a) Вычислить интеграл 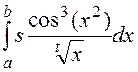 методом правых прямоугольников, воспользовавшись критерием двойного пересчета с точностью e = 10^–6   при        a = 0,1; b = 0,7; s = 4; t = 3. Вычисление значения функции в точке и вычисление интеграла оформить в виде функции.

b) Для заданных функций f(x) вычислить корень уравнения  на отрезке [a; b] с точностью e = 10^–6, используя  метод половинного деления и выполнив предварительно отделение корней:

  1. f(x) = (x-1)² - 3;  a = -2;  b = 1;

2*. f(x) = ;  a = 0;  b = 1;  sÎ[1,95; 2],   Ds = 0,01.

Вычисление корня уравнения оформить в виде функции с функциональным параметром, параметры a, b, e, s – в виде  аргументов по умолчанию. Результат представить в виде таблицы (s – значение параметра, х – вычисленный корень уравнения, f(x) – значение функции в найденной точке х, k_iter – количество итераций цикла для получения корня с заданной точностью).

Вариант 5.

a) Вычислить интеграл 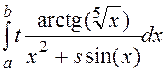 методом левых прямоугольников, воспользовавшись критерием двойного пересчета с точностью e = 10^–6  при  a = 0,1; b = 1,2; s = 0,1; t = 1,4. Вычисление значения функции в точке и вычисление интеграла оформить в виде функции.

b) Для заданных функций f(x) вычислить корень уравнения  на отрезке