Массивы. Обработка матрицы по столбцам. Обработка всей матрицы. Обработка части матрицы. Преобразование матрицы

Обработка части матрицы: к такому типу отнесем задачи, в которых выполняется обработка элементов главной или побочной диагонали квадратной матрицы, объявленной, например, так: const n=5; int A[n][n];

Структура циклов останется такой же, как при решении аналогичной задачи для одномерного массива. Например, для нахождения среднего значения главной диагонали необязательно писать два вложенных цикла:

double  Sum=0;

for (int i=0; i<n; i++)

   for(int j=0; j<n; j++)

if (i==j) Sum +=A[i][j];

Sum /=n;

Так как для элементов главной диагонали оба индекса одинаковы, то это можно выполнить компактнее с помощью одного цикла:

double Sum=0;

for (int i=0; i<n; i++)

Sum +=A[i][i];

Sum /=n;

Для обработки побочной диагонали необходимо найти зависимость второго индекса от первого. Легко видеть, что сумма индексов равна n-1. Поэтому второй индекс равен n-1-i, и соответствующая часть программы будет такой:

double Sum=0;

for (int i=0; i<n; i++)

Sum +=A[i][n-1-i];

Sum /=n;

Верхний треугольник квадратной матрицы относительно главной диагонали – это элементы, у которых i<j, если главная диагональ не включается, или i < =j, если включается. Аналогично определяется нижний треугольник, относительно главной диагонали и треугольники относительно побочной диагонали.

Для обработки таких треугольников необходимо определить, как изменяются индексы. В произвольной i-ой строке индекс j  изменяется от i до n-1. Поэтому, например, подсчет количества нулевых элементов верхнего треугольника, включая и главную диагональ, будет выглядеть следующим образом:

int K0=0;

for (int i=0; i<n; i++)

   for (int j=i; j<n; j++)

if (A[i][j] ===0)   K0++;

Если саму главную диагональ анализировать не надо, то заголовок внутреннего цикла будет выглядеть так:

for (int j=i+1; j<n; j++)

Подсчет количества нулевых элементов нижнего треугольника  относительно побочной диагонали выглядит так:

int K0=0;

for (int i=0; i<n; i++)

for (int j=n-i-1; j<n; j++)

if (A[i][j] ===0)   K0++;

5. Преобразование матрицы

Перестановка двух строк, номера которых n1 и n2 заданы, выполняется следующим образом:

int R;

for (int j=0; j<m; j++)

{R=A[n1][j]; 

A[n1][j]= A[n2][j];

A[n2][j]=R;}

Перестановка двух столбцов, номера которых m1 и m2 заданы, выполняется следующим образом:

int R;

for (int i=0; i<n; i++)

{R=A[i][m1]; 

A[i][m1]= A[i][m2];

A[i][m2]=R;}

Удаление k-ой строки  выполняется так:

for (int i=k; i<n-1; i++)

   for (int j=0; j<m; j++)

A[i][j] =A[i+1][j];

Здесь на место k-ой строки помещаем каждый элемент (k+1)-ой строки, на место (k+1)-й – (k+2)-ю и т.д. Таким образом, все строки, начиная с (k+1)-ой, «поднимаем на одну вверх». При этом объем зарезервированной для матрицы памяти не изменяется. Физически мы ни одну строку из памяти не удалили. Но после удаления одной строки, количество обрабатываемых строк на одну уменьшается. Последняя строка в обработке уже не должна участвовать.

Для вставки новой строки после k-й строки матрицы необходимо:

1. объявить массив как int A[n+1][m], так как после вставки количество строк увеличится;

2. все строки от k-й   до предпоследней переместить вниз:

for (int i=n-1; i>=k+1; i--)

for (int j=0; j<m; j++)

A[i+1][j] =A[i][j];

3. на место освободившейся (k+1)-й строки поместить вставляемую строку, например, одномерный массив В такой же размерности m, что и строка матрицы:

for (int j=0; j<m; j++)

A[k+1][j] =B[j];

Если новую строку надо вставлять в соответствии с некоторым условием (например, в строке больше половины нулей) после каждой строки, то матрицу надо объявить так: int A[2*n][m]. В этом случае резервируется максимальный объем памяти в предположении, что после каждой строки надо будет вставлять новую. Очевидно, что память в данном случае используется неэффективно. Это характерно и для случая удаления строк. На практике такое преобразование эффективнее выполнять с помощью динамических матриц или списков.

6. Построение матриц

Элементы матрицы можно задать по некоторому специальному правилу в зависимости от ее индексов. Например:

for (int i=0; i<n; i++)

   for (int j=0; j<m; j++)

A[i][j] =(i+1)*(j+1);

При построении матрицы можно использовать одно число. Например, построим матрицу А для заданных значений x и n:

Алгоритм следующий: очередной элемент «периметра матрицы» получаем так: умножаем предыдущий элемент на х и помещаем его в первую и последнюю строки, в первый и последний столбцы. Для этого достаточно одного цикла. Все «центральные» элементы обнуляем.

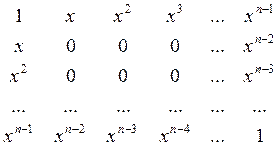
const n=5;

double x, A[n][n], T;

cin >> x;

A[0][0] = A[n-1][n-1] =1;

T=1;

for (int i=1; i<n; i++)

{T *=x;

A[0][i] =                 //элементы 0-й строки

A[i][0] =                 //элементы 0-го столбца

A[n-1][n-1-i] =       //элементы (n-1)-й строки

A[n-1-i][n-1] = T;   //элементы (n-1)-го столбца

}

for (int i=1; i<n-1; i++)

            for (int j=1; j<n-1; j++)

A[i][j]=0;

Матрицу можно построить, используя один или несколько одномерных массивов. Например, задано b[n]. Сформировать матрицу по следующему правилу:

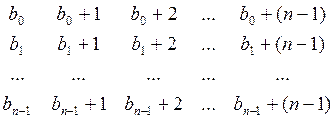
В таких задачах необходимо установить, от чего и как зависят индексы