Промышленность \ Технические средства автоматизации

Исследование системы автоматического управления. Оптимальные настройки регулятора в непрерывном варианте управления в зависимости от параметров объекта

Страницы работы

29 страниц (Word-файл)

Скачать файл

Уважаемые коллеги! Предлагаем вам разработку программного обеспечения под ключ.

Опытные программисты сделают для вас мобильное приложение, нейронную сеть, систему искусственного интеллекта, SaaS-сервис, производственную систему, внедрят или разработают ERP/CRM, запустят стартап.

Сферы - промышленность, ритейл, производственные компании, стартапы, финансы и другие направления.

Языки программирования: Java, PHP, Ruby, C++, .NET, Python, Go, Kotlin, Swift, React Native, Flutter и многие другие.

Всегда на связи. Соблюдаем сроки. Предложим адекватную конкурентную цену.

Заходите к нам на сайт и пишите, с удовольствием вам во всем поможем.

Фрагмент текста работы

Министерство высшего и среднего профессионального образования РФ.

Санкт-Петербургский Государственный Технологический

Университет Растительных Полимеров.

Кафедра автоматизированного электропривода и электротехники.

КУРСОВАЯ РАБОТА

ПО КУРСУ <ТАУ>.

Исследование системы автоматического

управления.

Выполнил студент группы 533 Проверил

. доцент

Санкт-Петербург

2003.

Задача курсовой работы.

Рассчитать оптимальные настройки регулятора в непрерывном варианте управления в зависимости от параметров объекта, сравнить качественные показатели переходных процессов САУ.

Выбрать систему с наилучшими показателями качества переходного процесса.

Исходные данные для выполнения курсовой работы.

а) Система автоматического управления.

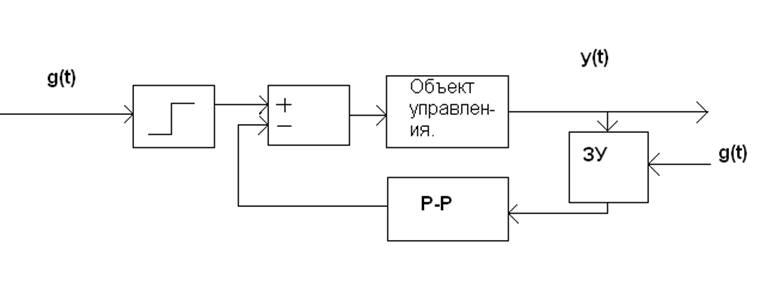
б) Уравнение объекта: a1dxвых/dt+ a2xвых=bxвх;

в) Значение Тоб, τоб, Коб.

Тоб - постоянная времени объекта;

Коб – коэффициентусиленияобъекта;

Τоб – запаздывание объекта;

х(t) – возмущающее воздействие;

y(t) – выходной параметр;

g(t) – задание;

р-р – регулятор;

T_об, с	τ_об,с	к_об
100	50	8

Исследование объекта управления.

1.1 Вывод дифференциального уравнения объекта.

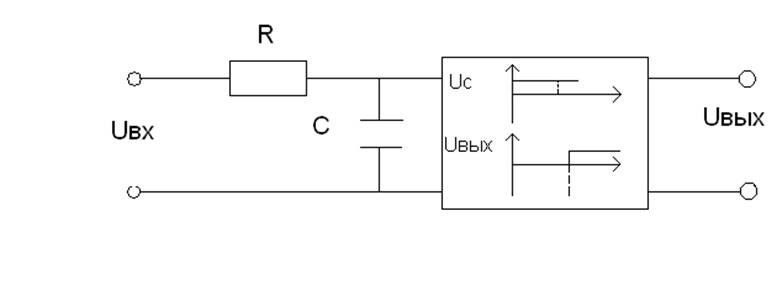
Рис.1. Схема исследуемого объекта.

Uвх=IR+Uc; i=cdUc/dt

Uвх=RCdUc/dt+Uc;

TdUc/dt+Uc=KUвх Uвх, где T=RC, K=1.

С учетом запаздывания τ уравнение объекта:

TdUвых/dt+Uвых=KUвх(t-τ).

Значение T=RC, τ, Kзадаются преподавателем.

Исследование объекта и САУ на ЭВМ.

Вывод передаточной функции объекта.

a1dxвых/dt+ a2xвых=bxвх;

a1/a2*dxвых/dt+xвых=b/a2xвх;

Tоб=a1/a2, Kоб= b/a2,

Tоб*dxвых/dt+xвых= Kобxвх;

TобPxвых(P)+Xвых(P)=Kобxвх(P);

xвых(P)/xвх(P)[TобP+1]=Kоб;

W(P)об=Kоб/TобP+1;

W(P)об=0.8/0.002P+1;

Cучетом запаздывания:

W(P)об=0.8/0.002P+1*e^-0,1Pоб;

Вывод амплитудно-фазовой, амплитудно-частотной, фазо-частотной и логарифмической характеристики объекта.

τоб=0;

Амплитудно-фазовая характеристика:

W(jω)=Kоб/√Tоб^2+ω^2+1*e^-arctgTобω;

W(jω)=0.8/√0.000004ω^2+1*e^-arctg0.002ω;

Амплитудно-частотная характеристика:

A(ω)=Kоб/√Tоб^2ω^2+1;

A(ω)=0.8/√0.000004ω^2+1;

Фазо-частотноя характеристика:

φ(ω)=-arctgTобω;

φ(ω)=-arctg0.002ω;

Логарифмическая характеристика:

L(ω)=20lg-20lg√Tоб^2+ω^2+1;

L(ω)=20lg-20lg√0.000004ω^2+1;

τоб≠0

Амплитудно-фазовая характеристика:

W(jω)=Kоб/√Tоб^2+ω^2+1*e^-arctgTобω-τобω;

W(jω)=0.8/√0.000004ω^2+1*e^-arctg0.002ω-0.1ω;

Амплитудно-частотная характеристика:

A(ω)=Kоб/√Tоб^2ω^2+1;

A(ω)=0.8/√0.000004ω^2+1;

Фазо-частотноя характеристика:

φ(ω)=-arctgTобω-τобω;

φ(ω)=-arctg0.002ω-0.1ω;

Логарифмическая характеристика:

L(ω)=20lg-20lg√Tоб^2+ω^2+1;

L(ω)=20lg-20lg√0.000004ω^2+1;

Переходная характеристика объекта:

Xвых(t)=Kоб(1-et^Tоб); Xвых(t)=0.8(1-et^0.002);

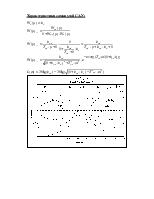
В результате исследования объекта были получены следующие зависимости:

1. Переходная характеристика.

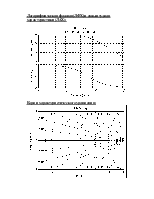
2. Амплитудная характеристика:

3. Логарифмическая характеристика:

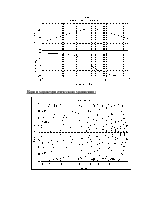
4. Амплитудно-фазовая характеристика.

Исследование объекта управления.

Структурная схема объекта:

τоб=0

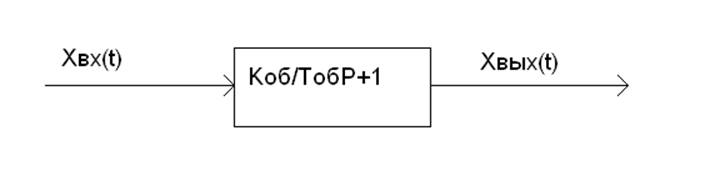
τоб≠0

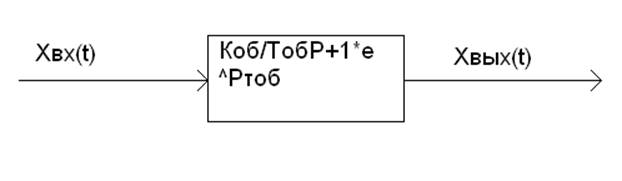
При моделировании объекта на ЭВМ необходимо определить:

1. Переходную характеристику при τоб=0 и при τоб≠0.

2. АФХ, ЛФХ, ЛАХ.

3. Определить Тоб, τоб и Коб и сравнить с заданным.

1. Исследование П-регулятора.

1.1. Объект имеет нулевое запаздывание: τ=0[с].

Рис. 1. Схема системы регулирования с П-регулятором и объектом регулирования, которому соответствует запаздывание τ=0[с].

Переходные процессы САУ.

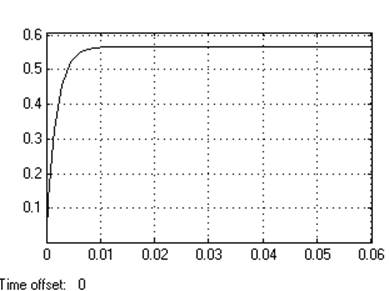Кр=0.5

Динамическое отклонение…нет.

Статическое отклонение...≈7.2℅

Время регулирования …0.01[c].

Динамический коэффициент регулирования………………0.51

Перерегулирование………….нет

Устойчивость………………….да

Кр=5

Динамическое отклонение…нет.

Статическое отклонение...≈3,6℅

Время регулирования …0.01[c].

Динамический коэффициент регулирования………………0,53

Перерегулирование………….нет

Устойчивость…………………да

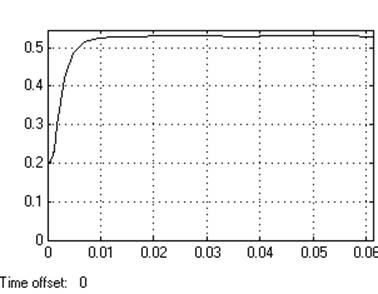
Кр=20

Динамическое отклонение…нет.

Статическое отклонение...≈1,8℅

Время регулирования …0.013[c].

Динамический коэффициент регулирования………………0,54

Перерегулирование………….нет

Устойчивость…………………да

1.2. Объект имеет запаздывание τ=0,1[c].

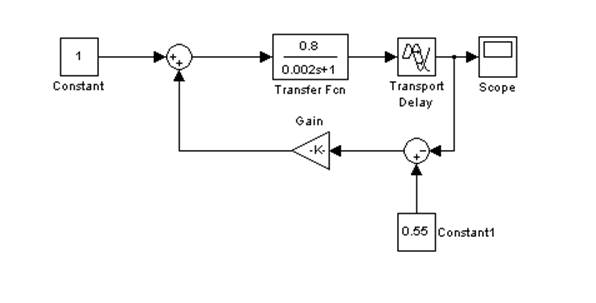
Переходные процессы САУ.

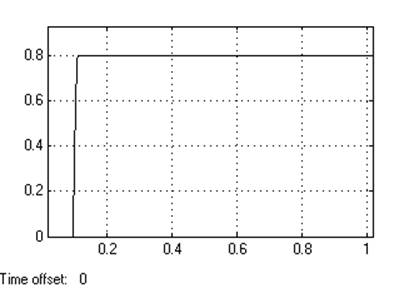
Кр=0,001

Динамическое отклонение…нет.

Статическое отклонение...≈9,1℅

Время регулирования …0.09[c].

Динамический коэффициент регулирования……………….0,5

Перерегулирование…………нет

Устойчивость…………………да

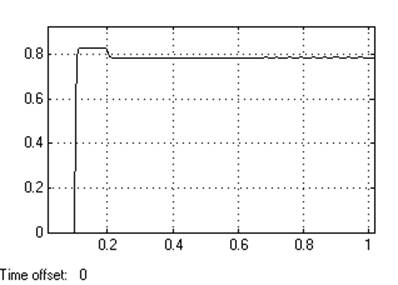Кр=0,07

Динамическое отклонение…нет.

Статическое отклонение...≈1,8℅

Время регулирования …0.023[c].

Динамический коэффициент регулирования………………0,54

Перерегулирование………….нет

Устойчивость…………………да

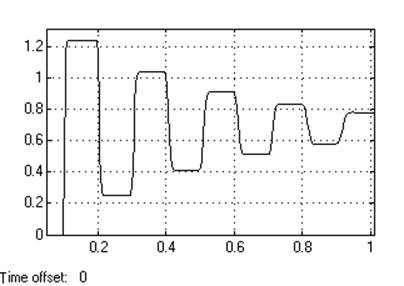Кр=1

Динамическое отклонение…0,26.

Статическое отклонение.......≈3℅

Время регулирования …...0.87[c].

Динамический коэффициент регулирования……………….0,78

Перерегулирование………….50℅

Устойчивость…………………..да

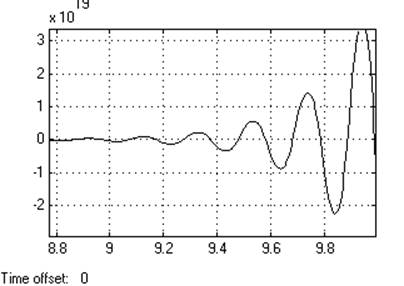
Кр=2

Динамическое отклонение…???.

Статическое отклонение.......???.

Время регулирования …...+∞[c].

Динамический коэффициент регулирования………………???

Перерегулирование………100℅

Устойчивость……….граничная

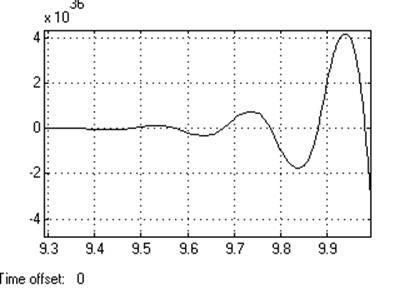
Кр=3

Динамическое отклонение…---.

Статическое отклонение.......---.

Время регулирования ……...---.

Динамический коэффициент регулирования………………---.

Перерегулирование…….>100℅

Устойчивость…………… нет.

2. Исследование И-регулятора.

2.1.Объект имеет запаздывание τ=0[c].

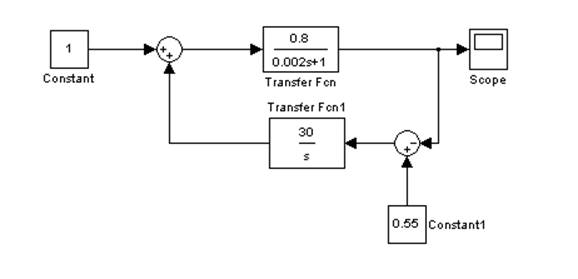
Рис. 3. Схема системы регулирования с И-регулятором и объектом регулирования, которому соответствует запаздывание τ=0[c].

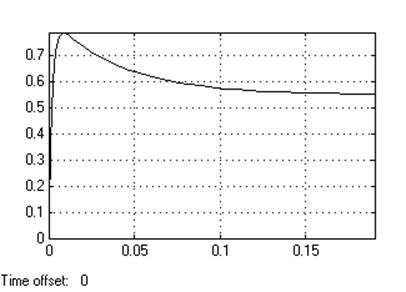
Кр=30

Динамическое отклонение….нет.

Статическое отклонение…..≈0℅.

Время регулирования………0.17.

Динамический коэффициент регулирования……………....0.55.

Перерегулирование………….нет.

Устойчивость…………………да.

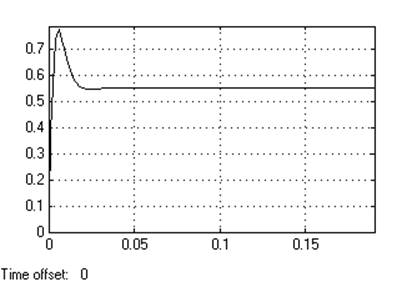Кр=235

Динамическое отклонение….0.11

Статическое отклонение…...≈0℅.

Время регулирования……0.03[c].

Динамический коэффициент регулирования……………….0.66.

Перерегулирование…………..8℅.

Устойчивость………………….да.

=350

Динамическое отклонение….0.13

Статическое отклонение…...≈0℅.

Время регулирования……0.025[c].

Динамический коэффициент регулирования……………….0.68.

Перерегулирование………….12℅.

Устойчивость…………………..да.

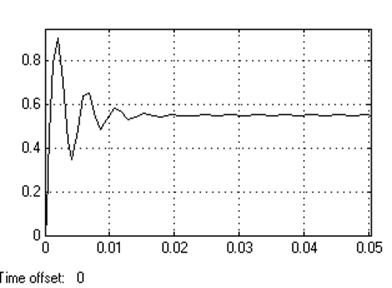
Кр=5000

Динамическое отклонение….0.35

Статическое отклонение…...≈0℅.

Время регулирования……0.02[c].

Динамический коэффициент регулирования……………….0.09.

Перерегулирование………….70℅.

Устойчивость………………….да.

2.2. Объект имеет запаздывание: τ=0,1[c].

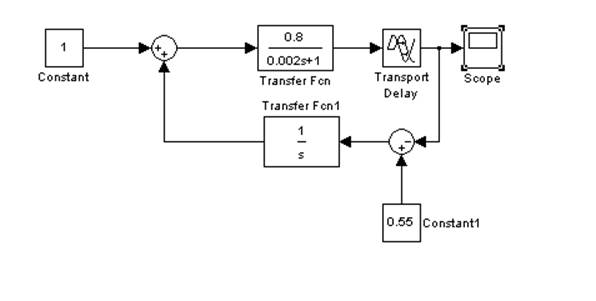
Рис. 4. Схема системы регулирования с И-регулятором и объектом регулирования, которому соответствует запаздывание τ=0,1[c].

Процессы автоматической системы.

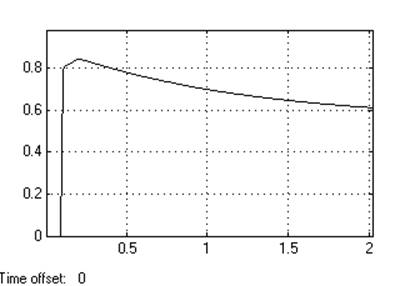
Кр=1

Динамическое отклонение….нет

Статическое отклонение…...≈0℅.

Время регулирования……2,00[c].

Динамический коэффициент регулирования……………….0.55.

Перерегулирование………….нет.

Устойчивость………………….да.

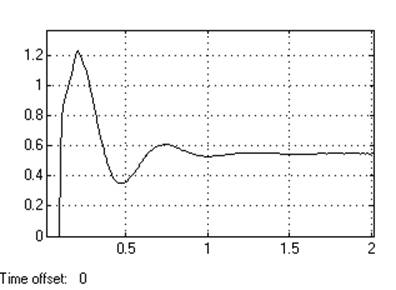
Кр=10

Динамическое отклонение….0.14

Статическое отклонение…...≈0℅.

Время регулирования……..1,25[c].

Динамический коэффициент регулирования……………….0.79.

Перерегулирование………….10℅.

Устойчивость………………….да.

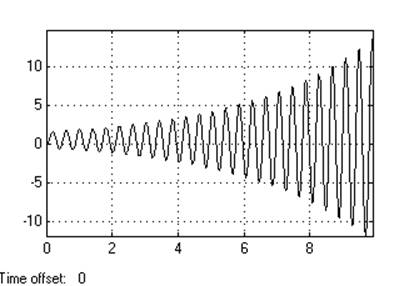
Кр=20

Динамическое отклонение….0.55

Статическое отклонение…...≈0℅.

Время регулирования……….+∞[c].

Динамический коэффициент регулирования………………..1.1.

Перерегулирование………….60℅.

Устойчивость………………….да.

Динамическое отклонение….<?>

Статическое отклонение….....<?>

Время регулирования……..+∞[c].

Динамический коэффициент регулирования………………..<?>

Перерегулирование………..100℅.

Устойчивость…………граничная.

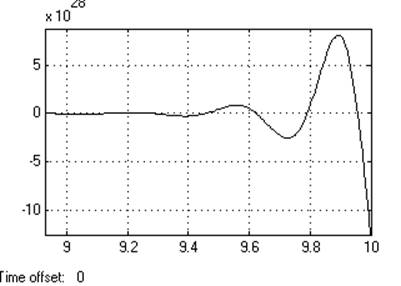
Кр=50

Динамическое отклонение….---.

Статическое отклонение…....---.

Время регулирования……….---.

Динамический коэффициент регулирования……………….---.

Перерегулирование…… >100℅.

Устойчивость……………….нет.

3. Исследование ПИ-регулятора.

3.1. Объект имеет запаздывание τ=0[c].

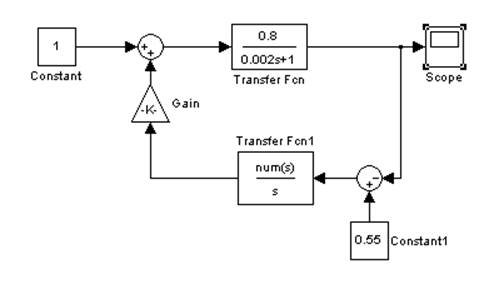
Рис. 5. Схема системы регулирования с ПИ-регулятором и объектом регулирования, которому соответствует запаздыванию τ=0[c].

Переходные процессы автоматической системы.

Примечание:

1) Путем увеличения параметра усилительного звена можно увеличить коэффициент усиления изодромного звена (Кр) и наоборот.

2) Путем увеличения числа перед оператором (S) в числителе выражения, характеризующего второе звено, можно увеличить время изодрома (Ти) и наоборот.

3) Величина (К1) характеризует пропорциональную состовляющую изодромного звена.

К1=0,01

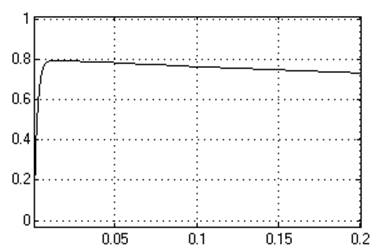Кр=200

Ти=0,00005

Динамическое отклонение….0,09.

Статическое отклонение…....≈0℅.

Время регулирования……0,2[c].

Динамический коэффициент регулирования………………./0.64.

Перерегулирование………… 10℅.

Устойчивость…………………..да.

К1=1

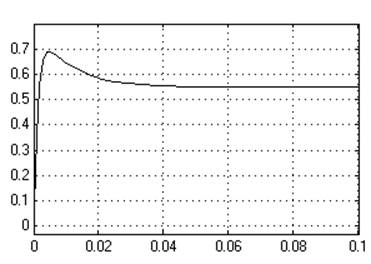Кр=200

Ти=0,005

Динамическое отклонение….0,05.

Статическое отклонение…....≈0℅.

Время регулирования……….0,45.

Динамический коэффициент

регулирования………………...0,6.

Перерегулирование………….. 0℅.

Устойчивость…………………..да

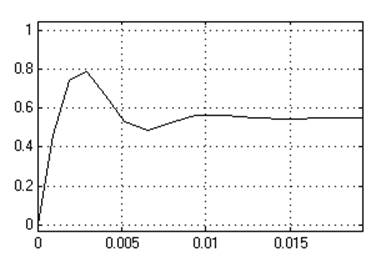К1=1

Кр=50

Ти=0,05[c]

Динамическое отклонение….нет.

Статическое отклонение…...≈0℅.

Время регулирования…....0,017[c].

Динамический коэффициент регулирования………………0.55.

Перерегулирование………… нет.

Устойчивость…………………да.

К1=1

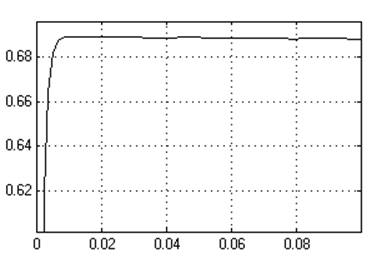Кр=0,1

Ти=10[c]

Динамическое отклонение….нет.

Статическое отклонение…...≈0℅.

Время регулирования……....>0.1

Динамический коэффициент регулирования……………….0,55.

Перерегулирование…………. нет.

Устойчивость…………………...да.

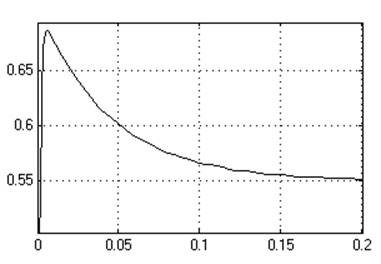
К1=1

Кр=50

Ти=0,02[c]

Динамическое отклонение….нет.

Статическое отклонение…...≈0℅.

Время регулирования…….0,02[c].

Динамический коэффициент регулирования……………….0,55.

Перерегулирование…………. нет.

Устойчивость…………………..да.

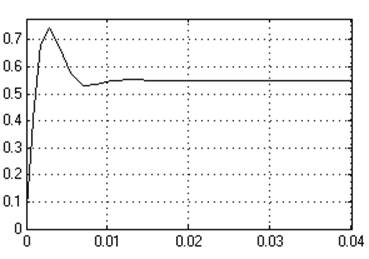К1=1

Кр=1500

Ти=0,000667

Динамическое отклонение….0,19.

Статическое отклонение…....≈0℅.

Время регулирования……0,015[c].

Динамический коэффициент регулирования………………0.74.

Перерегулирование……….. 40℅.

Устойчивость…………………да.

3.2. Объект имеет запаздывание τ=0,1[c].

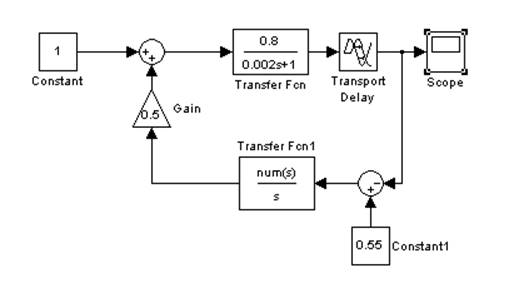
Рис. 6. Схема системы регулирование с ПИ-регулятором и объектом регулирования, которому соответствует запаздывание τ=0,1[c].

Путем изменения различным образом, параметров звеньев в цепи обратной связи, были получены следующие графические зависимости.

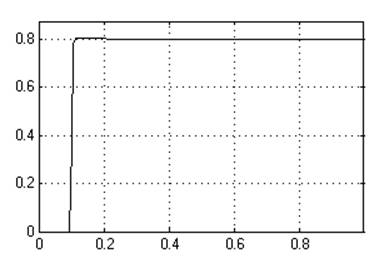
К1=0,007

Кр=0,5

Ти=0,014

Динамическое отклонение…..нет.

Статическое отклонение…....≈0℅.

Время регулирования………0,22[c].

Динамический коэффициент регулирования………………0.55.

Перерегулирование…………..нет.

Устойчивость…………………да

=0,007

Кр=1,8

Ти=0,00389

Динамическое отклонение….0,01.

Статическое отклонение…....≈0℅.

Время регулирования……0,1[c].

Динамический коэффициент регулирования………………0.56.

Перерегулирование………..…нет.

Устойчивость…………………..да

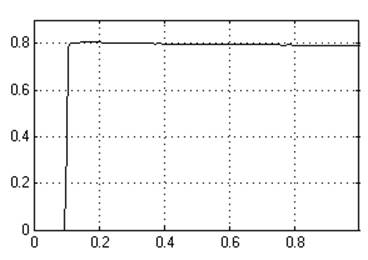
К1=0,007

Кр=10

Ти=0,0007

Динамическое отклонение….0,24.

Статическое отклонение…....≈0℅.

Время регулирования………..0,21[c].

Динамический коэффициент регулирования……………….0.79.

Перерегулирование……….. …7℅.

Устойчивость…………………да

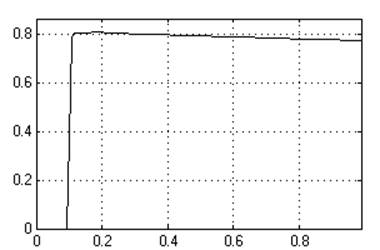
К1=0,007

Кр=30

Ти=0,0002333

Динамическое отклонение…<?>.

Статическое отклонение…...<?>.

Время регулирования…….0,93[c].

Динамический коэффициент регулирования………………<?>.

Перерегулирование……….100℅.

Устойчивость…………граничная.

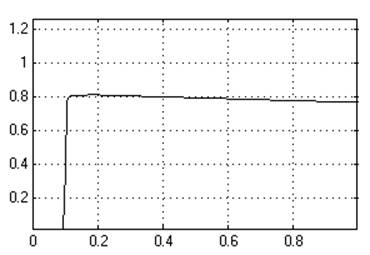К1=0,007

Кр=40

Ти=0,000175

Динамическое отклонение….----.

Статическое отклонение…....----.

Время регулирования……….0,88.

Динамический коэффициент регулирования……………….----.

Перерегулирование………..>100℅.

Устойчивость…………………нет

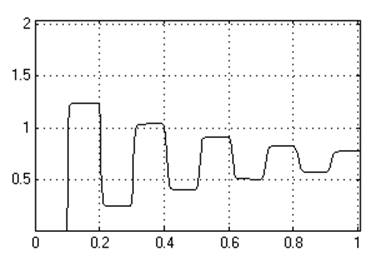К1=0,0007

Кр=0,07

Ти=0,01[c]

Динамическое отклонение…..нет.

Статическое отклонение…....≈0℅.

Время регулирования………0,92[c].

Динамический коэффициент регулирования………………0.55.

Перерегулирование…………..нет.

Устойчивость…………………..да

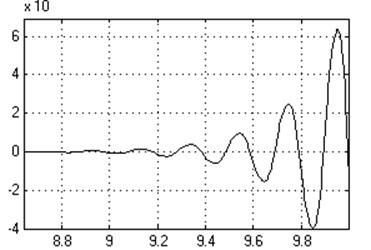
К1=1

Кр=0,07

Ти=14,285714

Динамическое отклонение….0,23.

Статическое отклонение…....≈0℅.

Время регулирования………+∞ [c].

Динамический коэффициент регулирования………………..0.78.

Перерегулирование…………. 40℅.

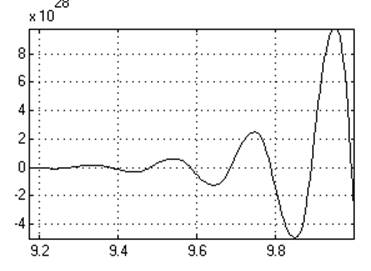Устойчивость……………………да

К1=2,0101

Кр=0,07

Ти=28.71571429

Динамическое отклонение…<?>.

Статическое отклонение…...<?>.

Время регулирования…….+∞[c].

Динамический коэффициент регулирования………………<?>.

Перерегулирование……….100℅.

Устойчивость…………граничная.

Характеристики замкнутой САУ:

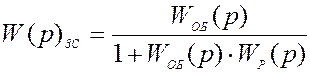
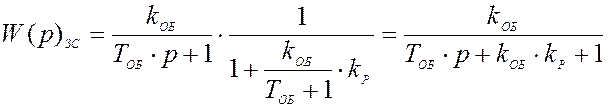
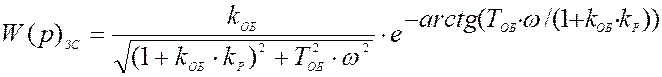
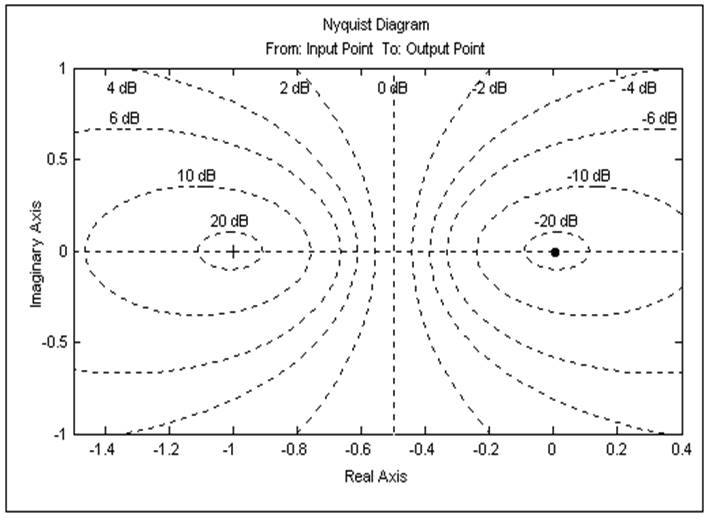
Логарифмическая фазовая(ЛФХ)и амплитудная характеристики(ЛАХ):

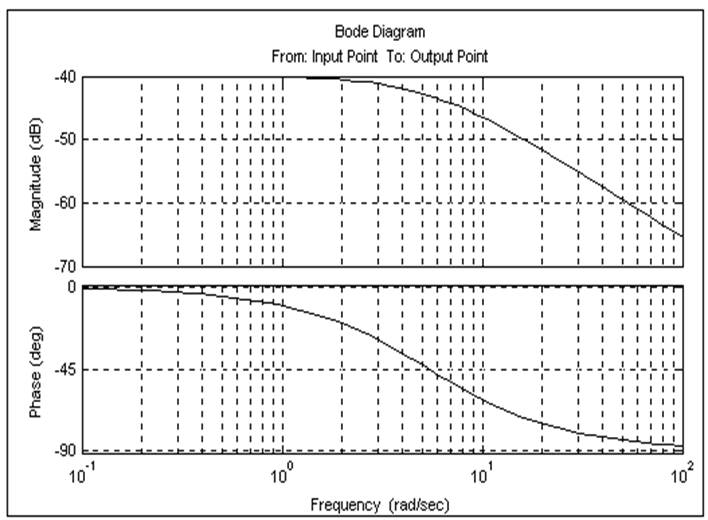Корни характеристического уравнения:

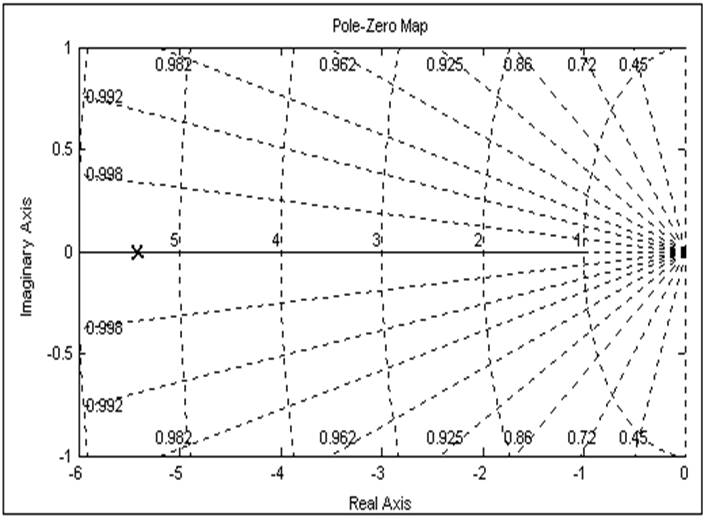
Характеристики замкнутой САУ:

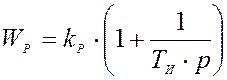
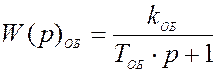
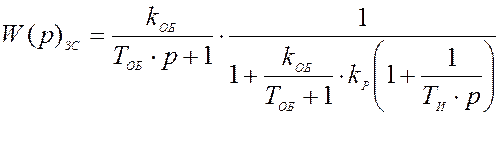
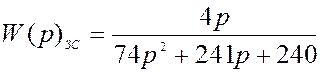
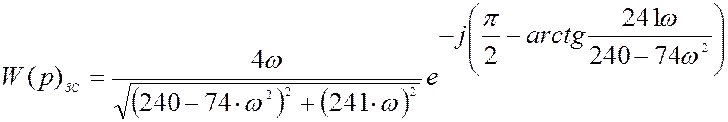
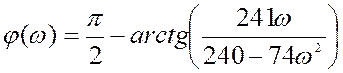
Амплитудно-фазовая характеристика:

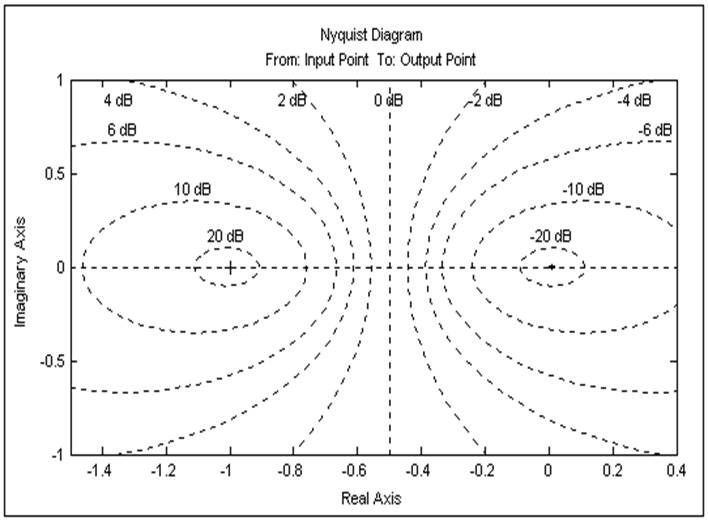
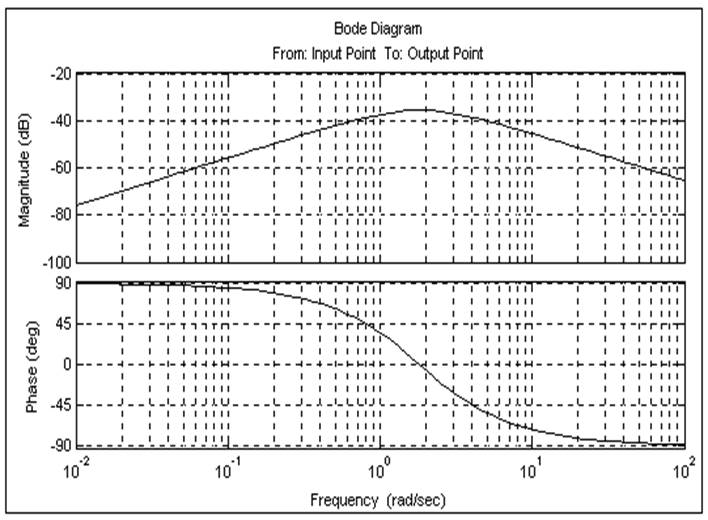
Корни характеристического уравнения:

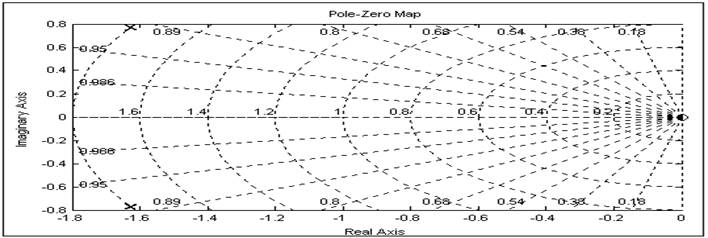
Графо-аналитический метод расчета настроек регулятора.

Построение АФХ объекта.

1-ый вариант

W(jω)=Kоб*e^-jωτоб/1+ jωТоб=А(ω)e^-jφ(ω);

где А(ω)= Kоб/√1+ jωТоб^2;

φ(ω)=-ωτоб-arctgωТоб;

ω, 1/с.	0	0,02	0,04	0,06	0,1	0,12	0,16	0,2
А(ω)	0,8	0,79	0,79	0,79	0,79	0,79	0,79	0,79
φ(ω),(рад)	0	-0,12	-0,25	-0,38	-0,64	-0,77	-1,03	-1,29

W(jω)=Kоб*e^-jωτоб/1+ jωТоб= 0,8*e^-j0,1ω/1+ j0,02ω;

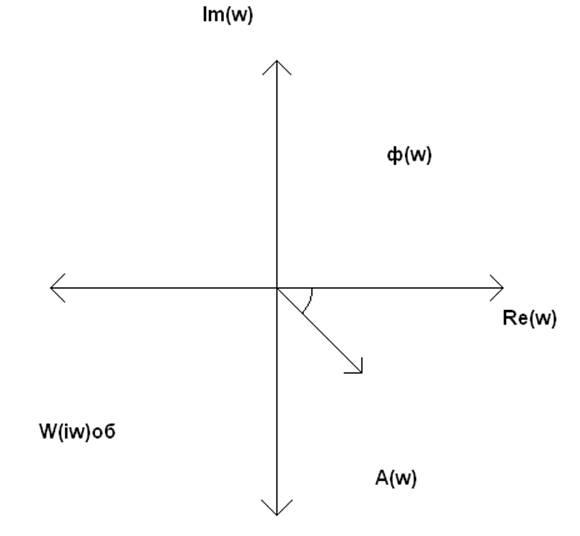
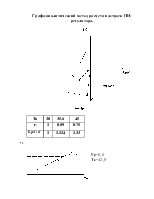
Графо-аналитический метод расчета настроек ПИ-регулятора.

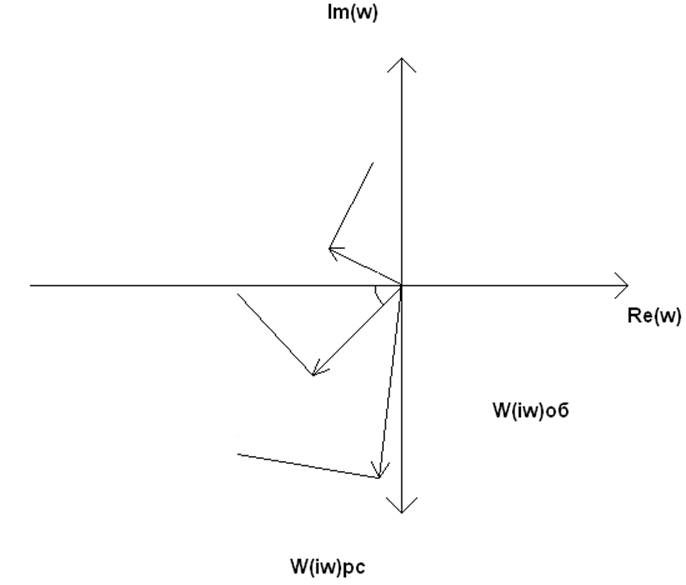
Ти	30	35.6	45
ri	1	0.89	0.75
Kp=1/ ri	1	1.124	1.33

Кр=1,1

Ти=32,5

Расчет настроек регулятора.

Типовой процесс регулирования: апериодический.

П-регулятор Коб=0,3/Коб*τоб/Тоб=0,3/0,8*0,1/0,02=0,075.

ПИ-регулятор Коб=0,7/Коб*τоб/Тоб=0,7/0,8*0,1/0,02=0,175.

Ти=0,6Тоб=0,6*0,02=0,012.

ПИД-регулятор Коб=0,95/Коб*τоб/Тоб=0,95/0,8*0,1/0,02=0,23.

Ти=2,4τоб=0,24.

Тпр=0,4τоб=0,04.

Типовой процесс регулирования: 20%-перерегулирование.

П-регулятор Кр=0,7/Коб*τоб/Тоб=0,7/0,8*0,1/0,02=0,175.

ПИ-регулятор Кр=0,7/Коб*τоб/Тоб=0,7/0,8*0,1/0,02=0,175.

Ти=0,7τоб =0,014.

ПИД-регулятор Кр=1.2/Коб*τоб/Тоб=1,2/0,8*0,1/0,02=0,3.

Ти=2,0τоб=2*0,1=0,2.

Тпр=0,4τоб=0,4*0,1=0,04.

min∫∆x^2выхс/t.

П-регулятор Кр=0.9/Тоб*τоб/Тоб=0.9/0.8*0.1/0.02=0.225.

ПИ-регулятор Кр=1/Тоб*τоб/Тоб=1/0.8*0.1/0.02=0.25.

Ти=Тоб=0.8.

ПИД-регулятор Кр=1.4/Коб*τоб/Тоб=1.4/0.8*0.1/0.02=0.35.

Ти=1.3τоб=1.3*0.1=0,35.

Тпр=0,5τоб=0,5*0,1=0,05.

Кр-коэффициент усиления регулятора;

τоб-запаздывание объекта;

Тоб-постоянная времени объекта;

δст-остаточное отклонение регулируемой величины после процесса регулирования;

Ти-время изодрома регулятора.

В процессе настройки П-регулятора, И-регулятора, ПИ-регулятора, было показано, что характер переходного процесса и, следовательно, качество регулирования определяется не только законом регулирования, но и значениями настройки регуляторов. При разных настройках одного и того же закона можно получить переходные процессы, отличающиеся друг от друга значениями перерегулирования, временем регулирования и т.д. Поэтому для оценки работы автоматической системы необходимо сравнивать отдельные показатели качества ее регулирования с какими-то процессами регулирования, принятыми за оптимальных настроек регулятора.

Вывод:

Об оптимальности регулятора можно судить, только если известны все составляющие данную систему объекты (или объект), а также все критерии и ограничения, которым должна удовлетворять данная система регулирования. К таким ограничениям можно, к примеру, отнести характер переходного процесса (время регулирования, максимальный динамический коэффициент отклонения и другие), также на САУ накладываются ограничения по надежности, простоте, и что в настоящее время особенно актуально по стоимости. Таким образом, систему можно назвать оптимальной, если