Гидродинамика вязкой жидкости. Стационарное течение жидкости. Условие неразрывности струи. Уравнение Бернулли и его следствия

ЛЕКЦИЯ №8

ГИДРОДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ.

1.Стационарное течение жидкости. Условие неразрывности струи.

Гидродинамика - раздел физики, в котором изучают вопросы движения жидкостей (несжимаемых) и взаимодействие их при этом с окружающими твердыми телами.

К жидкостям относятся вещества, которые по своим свойствам занимают промежуточное положение между газами и твердыми телами. Жидкие среды составляют наибольшую часть организма, их перемещение обеспечивает обмен веществ и снабжение клеток кислородом, поэтому механические свойства и течение жидкостей представляют собой интерес для медиков и биологов.

Рассмотрим установившееся или стационарное течение жидкости, т.е. такое течение, при котором скорости частиц жидкости в каждой точке потока со временем не изменяются.

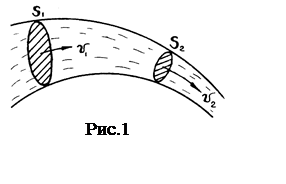Стационарное течение характеризуют линиями тока - воображаемыми линиями, совпадающими с траекториями частиц. Касательные к линиям тока показывают направление вектора скорости частиц жидкости, густота этих графически изображенных линий пропорциональна скорости. Часть потока жидкости, ограниченная со всех сторон линиями тока, образует трубку тока или струю (рис. 1).

Выделим трубку тока настолько узкую, что скорости частиц J в любом ее сечении S, перпендикулярном оси трубки, можно считать одинаковыми по всему сечению. Так как скорость частиц направлена вдоль линии тока, то частицы жидкости не могут выходить за пределы этой трубки. Тогда объем D V несжимаемой жидкости, протекающий через любое сечение трубки в единицу времени, остается постоянным:

DV = J= const .                                      (1)

 Соотношение (1) выражает условие неразрывности струи, т.к. только при сплошном течении через любое сечение за одно и то же время проходят одинаковые объемы несжимаемой жидкости.

Тогда: J₁S₁ = J₂S₂ (см. рис.1), откуда 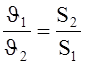, т.е. средние скорости течения в различных сечениях трубы  обратно пропорциональны площадям этих сечений.

Из условия неразрывности струи следует, что и для реальной жидкости при установившемся течении по трубе переменного сечения количество жидкости, протекающее за одно и то же время через любое сечение трубы, остается постоянным: Q = const. В частности, это с достаточно большой точностью выполняется и для кровотока в крупных кровеносных сосудах человека за время, равное нескольким, скажем трем, сердечным циклам, непосредственно следующих друг за другом.

2. Уравнение Бернулли и его следствия.

Одно из наиболее важных уравнений, используемых для описания движущихся жидкостей, было впервые получено швейцарским математиком и физиком Даниилом Бернулли (1700-1782 г.г.). Для вывода уравнения Бернулли предположил, что имеем дело с идеальной жидкостью. Это значит, что мы пренебрегаем любыми силами вязкого сопротивления и трения. Пусть жидкость течет совершенно плавно без каких-либо турбулентностей, т.е. течение жидкости стационарное. Более того, мы рассматриваем только несжимаемые жидкости, так что определенная масса жидкости будет занимать одинаковый объем, несмотря на положение или условия в потоке.

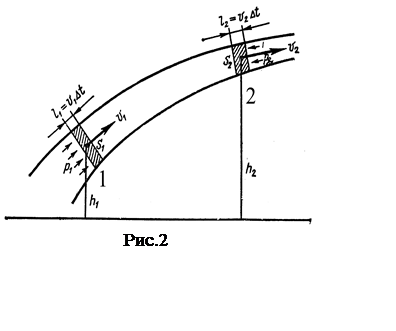Уравнение Бернулли можно вывести, используя закон сохранения энергии при протекании жидкости через трубу. Как показано на рис.2, трубка тока имеет различные площади поперечного сечения и различную высоту над некоторым исходным уровнем. Если совершить некоторую работу А над жидкостью, это вызовет изменение в потенциальной и кинетической энергии жидкости: А = D Е_п + D Е_к (2). Выделим в трубке тока достаточно малый объем жидкости DV массой m. Мы совершаем работу, действуя силой F₁ на количество жидкости в положении 1(см. рис. 2) и перемещая каждый малый элемент этого объема на величину единичного перемещения l₁  с постоянной скоростью J₁ . Так, объем DV₁ =l₁S₁ перемещен на расстояние l₁ и проделанная  над жидкостью работа равна F₁l₁. Каково влияние этого перемещения на жидкость, находящуюся в положении 2? Поскольку жидкость несжимаема, перемещение объема l₁S₁ на расстояние l₁ в положение 1 означает перемещение равного объема в положение 2. Поэтому количество жидкости, с площадью поперечного сечения S₂ смещается на расстояние l₂ c постоянной скоростью J₂, где S₁l₁ = S₂l₂. Объем жидкости в положении 2 движется вдоль трубы, толкая следующие слои жидкости. Сила F₂, действует при перемещении l₂, поэтому работа, совершаемая этим