Таким образом, передаточная функция регулятора (без фильтра) примет вид:
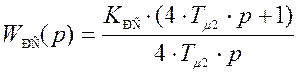
Структурная схема контура регулирования скорости, с учетом регулятора скорости, примет вид:
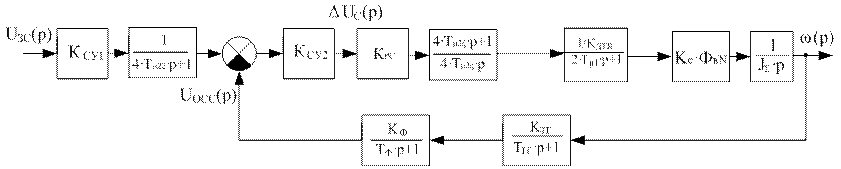
Рис. 6. Преобразованная структурная схема контура скорости
4. СТАТИЧЕСКИЙ РАСЧЕТ ЯКОРНОГО КАНАЛА
После синтеза регуляторов производят расчёт САУ в установившемся режиме, т.е. статический расчёт. Статический расчет производят с целью получения статической характеристики электропривода, расчёта недостающих коэффициентов передачи, определение статической ошибки и других технических показателей.
Статический расчет производят по структурной схеме в установившемся режиме, который получается при р = 0. Данную замену можно производить с условием, что не будет деления на ноль, и умножение на 0 передаточной функции. Получим преобразованную структурную схему рис. 7:
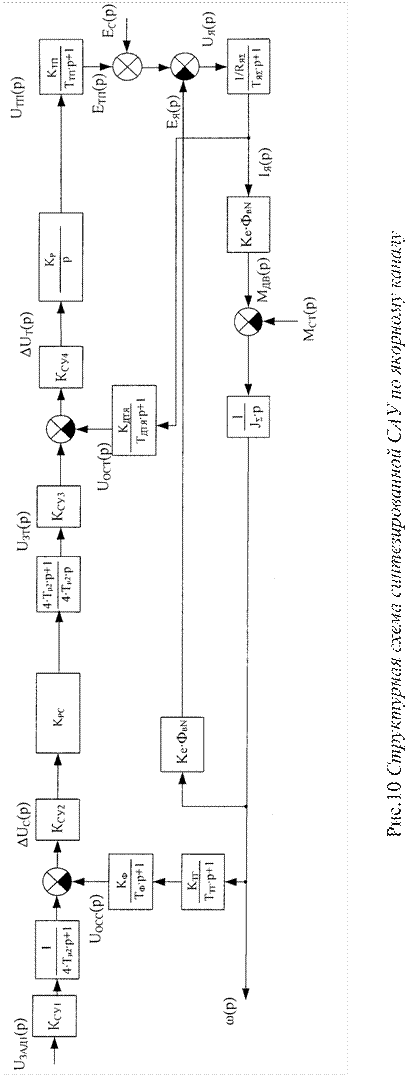
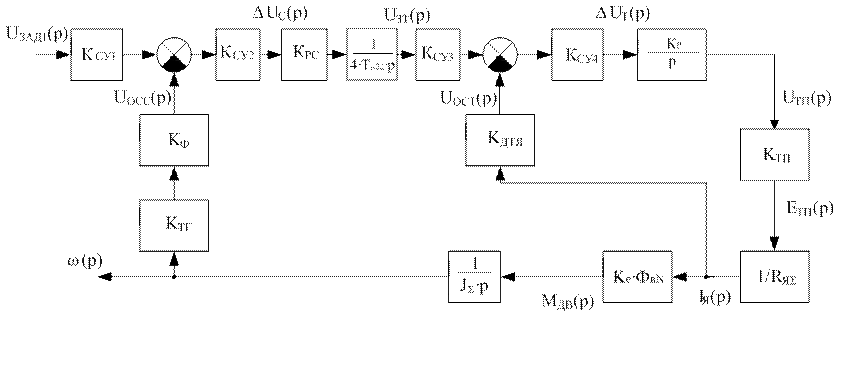Рис. 7. Преобразованная структурная схема
якорного канала
Используя правила структурного преобразования, преобразуем контур, охваченный обратной связью (контур тока):
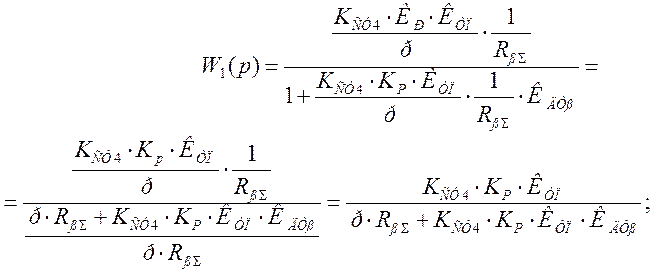
Положим р = 0:
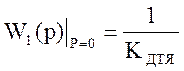
Преобразованная схема примет вид:
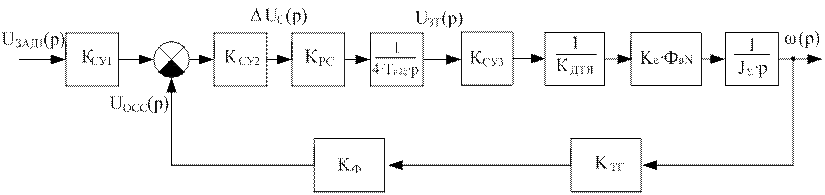
Рис. 8. Преобразованная структурная схема
Преобразуем полученную схему по правилам структурных преобразований и приведем ее к виду:
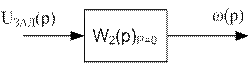
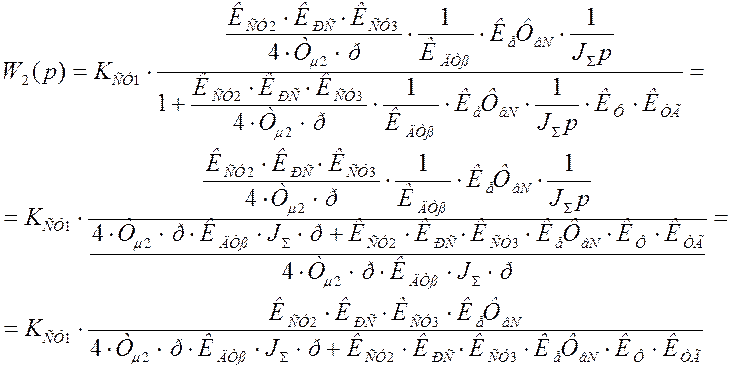
Положим р = 0:
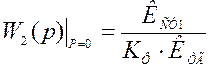
Окончательно получим структурную схему:
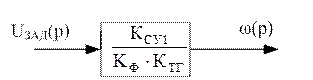
Тогда уравнение, описывающее статическую характеристику, будет иметь следующий вид:
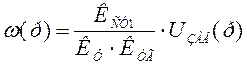
с учетом найденных коэффициентов получим:
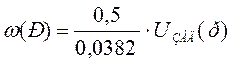
Задавая напряжение UЗАД от 0 до номинального значения построим статическую характеристику исследуемого канала:
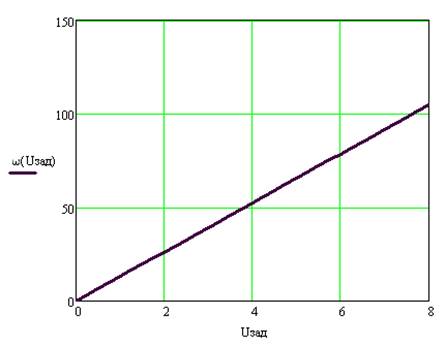
Рис. 9. Статическая характеристика
Произведем статический расчет для канала ω(МСТ). Преобразованная схема для данного канала имеет вид:
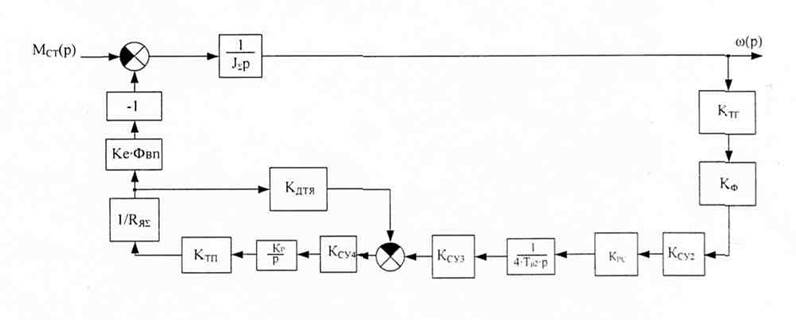
Используя правила структурных преобразований, приведем данную схему к схеме с передаточной функцией:
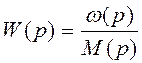при р
= 0
Преобразуем первую обратную связь:
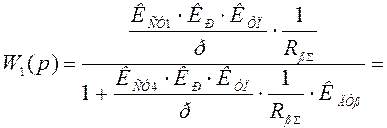
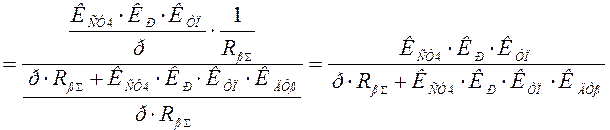
При р = 0 имеем:
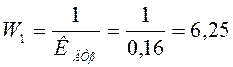
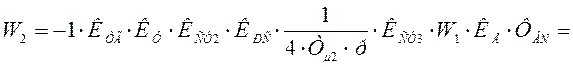
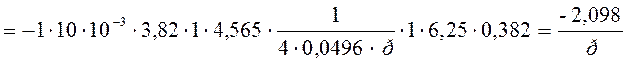
Преобразуем вторую обратную связь:
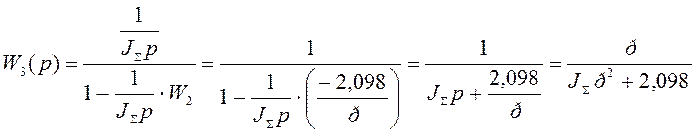
При р = 0 имеем:
W3 = 0
Следовательно, данная САУ не имеет статической ошибки по возмущению (моменту нагрузки).
Произведем статический расчет для канала ω(UС). Преобразованная схема для данного канала имеет вид:
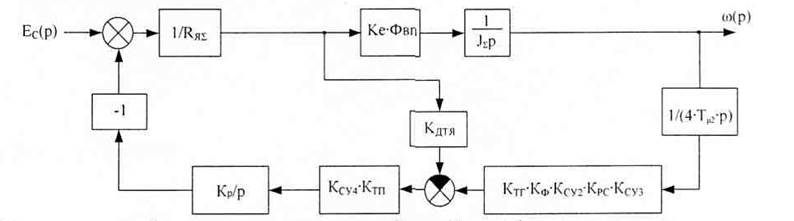
Используя правила структурных преобразований (перенос точки разветвления через звено на его выход) получим преобразованную схему:
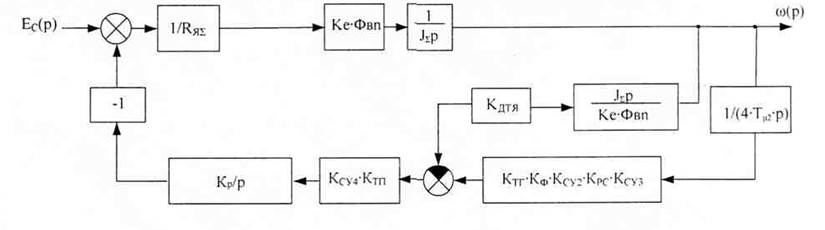
Используя правила структурных преобразований, приведем данную схему к схеме с передаточной функцией:
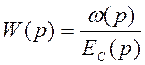при р = 0
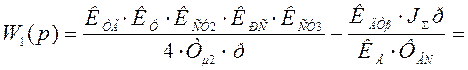
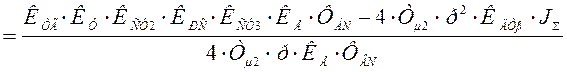
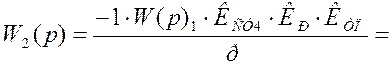
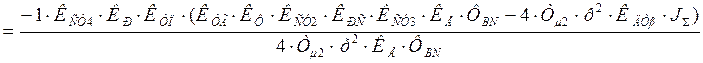
Тогда:
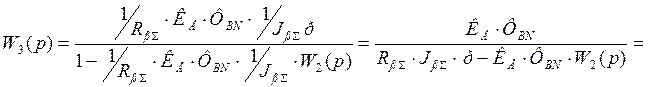
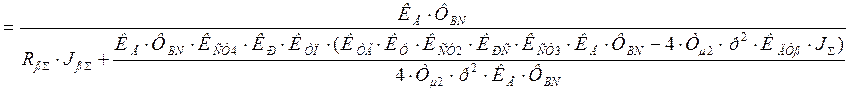После
преобразования, пологая р = 0 получим W3(p) = 0. Следовательно, данная САУ не имеет
статической ошибки по ЕС.
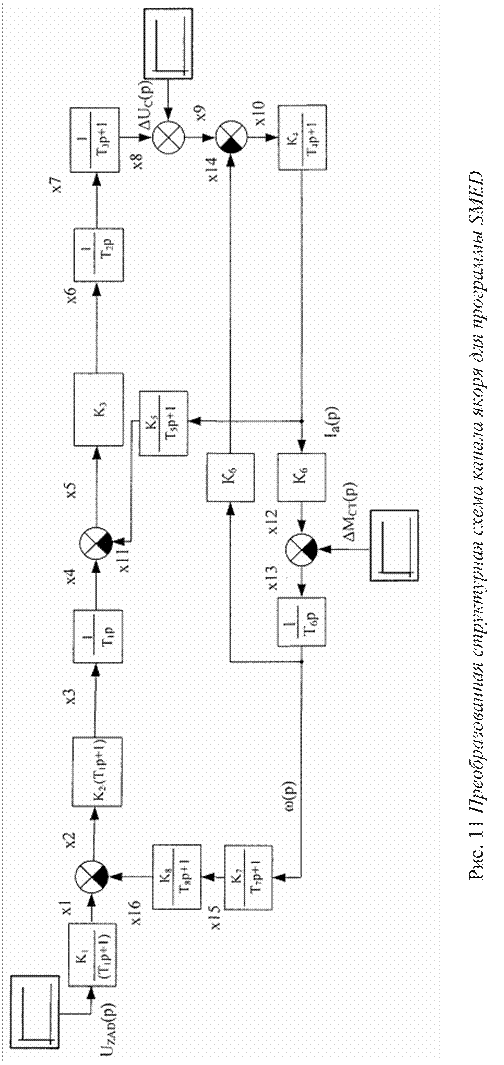
В данной схеме введены следующие обозначения:
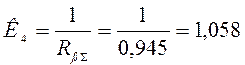
с
с
с
с
с
с
с
с
Скачки сигналов:
В
Н·м
В
Производя расчеты в программе SMED, получили следующие зависимости для контура тока:
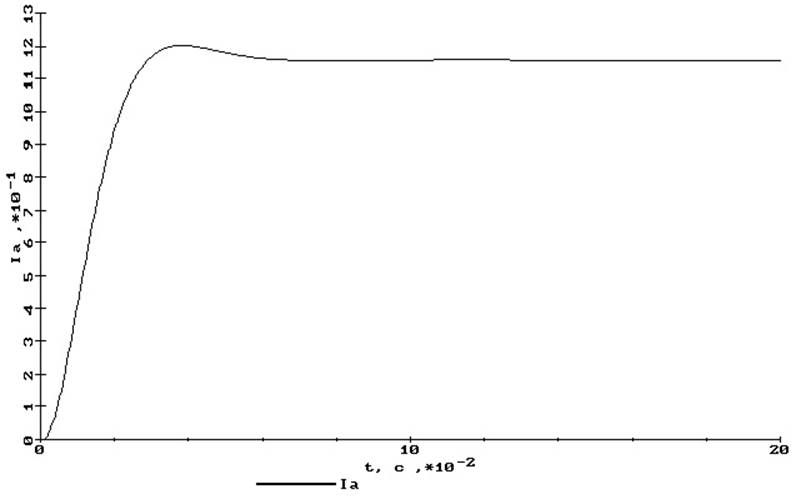
а)
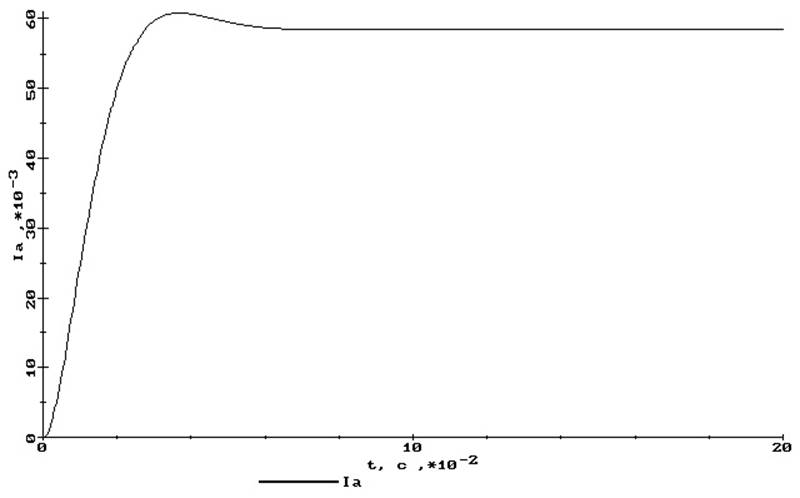
б)
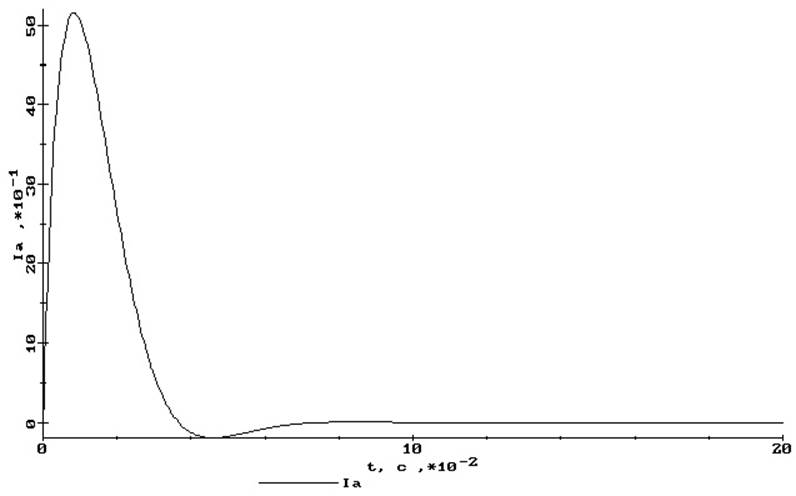
в)
Рис. 12 Переходные процессы контура регулирования тока якоря:
а) по заданию, б) по возмущению (от момента нагрузки),
в) от напряжения сети
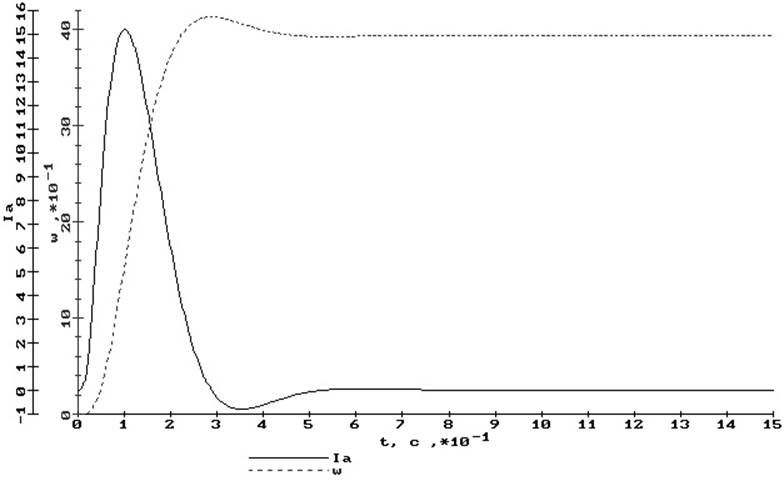
а)
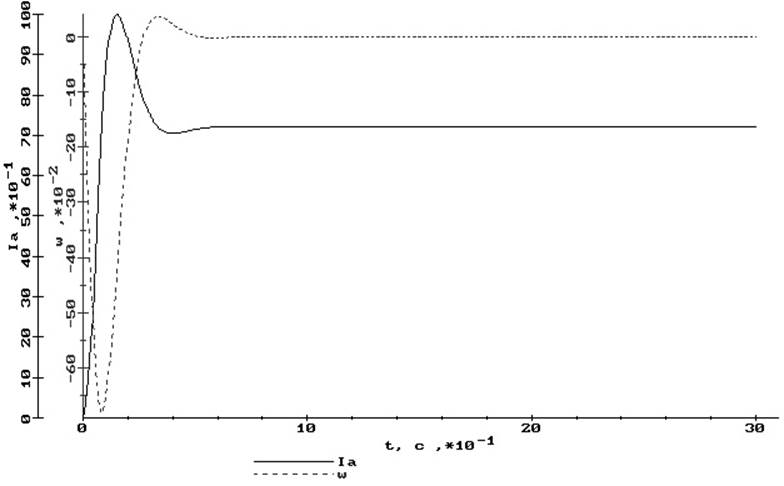
б)
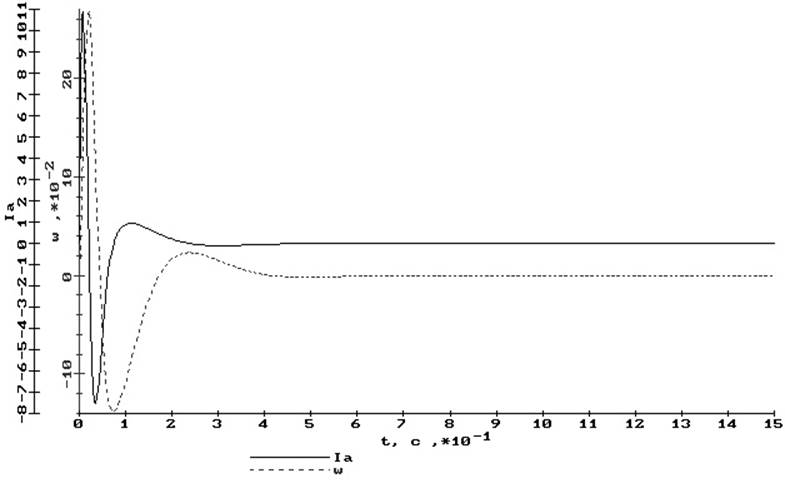
в)
Рис. 13 Переходные процессы якорного канала:
а) по заданию, б) по возмущению (от момента нагрузки),
в) от напряжения сети
5. АНАЛИЗ КАЧЕСТВА НАСТРОЙКИ РЕГУЛЯТОРА
После расчета переходных процессов можно оценить правильность синтеза структуры регуляторов и расчета их параметров, т.е. оценить качество настройки регуляторов.
В разделе 3.1 было указано, что оптимизация на технический оптимум (ТО) обеспечивает отсутствие статической ошибки по управлению (по возмущению статическая ошибка может быть или не быть), перерегулирование σ% = 4,3%, быстродействие tрег ≤ 4,2∙(2∙Тμ).
Улучшенный симметричный оптимум (УСО) устраняет статические ошибки по управлению и по возмущению, перерегулирование σ% <8,1%, время регулирования tрег ≤ 13,3·(2·Тμ). Эти показатели можно взять за контрольные и путем сравнения их с полученными по переходным процессам, сделать вывод о качестве настройки регуляторов.
На рисунках 5.1 – 5.2 представлены рассчитанные переходные процессы в канале регулирования электродвигателя со стороны якоря. Малые постоянные времени контура тока и контура скорости: Тμ1 = 0,0069 с, Тμ2 = 0,0496 с.
Так как регулятор тока настроен на ТО, то:
tрег1 = 4,2·2·Тμ1= 4,2·2·0,0069 = 0,058 с
Контур скорости настроен на УСО:
tрег2 = 13,3·2·Тμ2 = 13,3·2·0,0496 = 1,319 с.
Из переходных характеристик получим при обработки задания (рис.12а, 13а)
tрег1 = 0,008 с, tрег2 = 0,6 с а при обработке возмущения (от момента нагрузки) (рис. 12б, 13б)
tрег1 = 0,008 с, tрег2 = 0,6 с от напряжения в сети (рис. 12в, 13в)
tрег1 = 0,1 с, tрег2 = 0,5 с
Видно, что быстродействия тока контура и контура действия лучше, чем ожидаемое.
Перерегулирование по рис. 12а, 13а:
σ% = 4,2%, σ% = 7,2%, что меньше необходимого перерегулирования.
Дополнительно определим время первого перехода и время достижения максимума при отработки управления:
tПП1=30мс; tMAX1=38мс; tПП2=23мс; tMAX2=29мс и возмущения
tПП1=27мс; tMAX1=38мс; tПП2=90мс; tMAX2=160мс
Можно сделать вывод о хорошей настройке регулятора скорости и тока.
6. СИНТЕЗ ЭЛЕКТРИЧЕСКИХ СХЕМ РЕГУЛЯТОРОВ
В нашем случае регулятор тока якоря имеет следующую передаточную функцию:
.
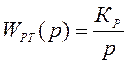Данную передаточную функцию можно представить в виде:
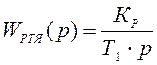, где 
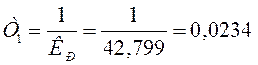с.
Регулятор тока представляет собой интегральный регулятор (И – регулятор):
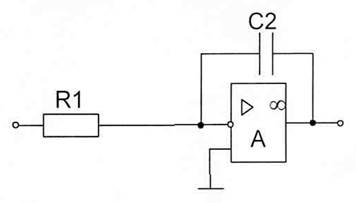
Рис. 14 Электрическая схема регулятора тока якоря
с
Выбираем из стандартного ряда: R2= 90 кОм, тогда
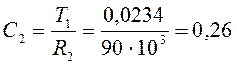мкФ
Из стандартного ряда выбираем С2=0,25 мкФ.
Регулятор скорости имеет следующую передаточную функцию:
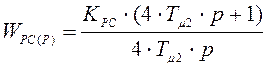
Регулятор скорости представляет собой пропорциональный регулятор
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
