






























синтеза внешнего контура контур тока заменяем эквивалентным звеном:
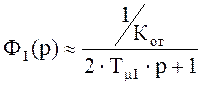
3) Регулятор натяжения.
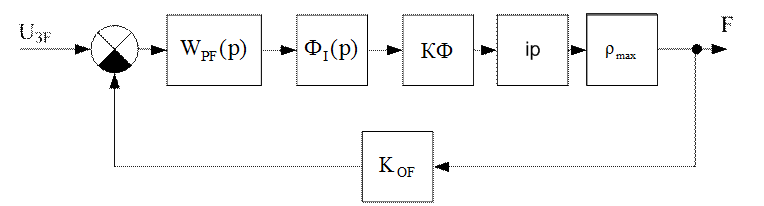
Рис. 5. Контур натяжения.
Коэффициент
обратной связи по натяжению: 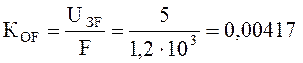 ;
;
Предаточная функция контура натяжения с учетом эквивалентной передаточной функции контура тока имеет вид:
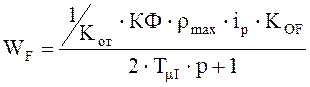
Тогда передаточная функция регулятора будет иметь вид:
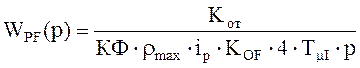
4) Регулятор потока.
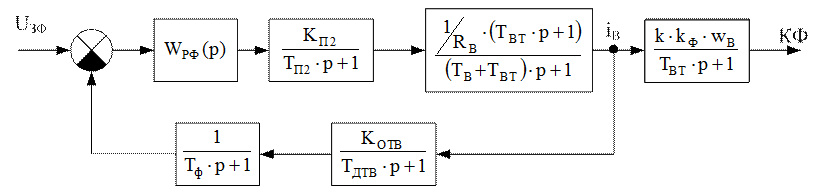
Рис. 6. Контур потока.
Ток
возбуждения равен: 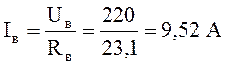 , тогда
коэффициент обратной связи будет равен:
, тогда
коэффициент обратной связи будет равен: 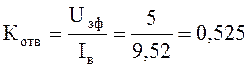 .
.
Для компенсации форсирующего звена в канале обратной связи установлен фильтр с параметрами: Тф = Твт = 0,0218 с.
Принимаем Тдтв = 0, а за малую постоянную времени контура принимаем:
Тμф = Тп2 = 0,01 с.
Для настройки на ТО необходим ПИ-регулятор:
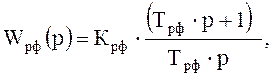
с параметрами:
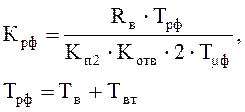
Поскольку в канале обратной связи присутствует апериодическое звено, постоянная времени которого не входит в малую постоянную времени контура, то передаточная функция замкнутого контура тока возбуждения будет иметь вид:
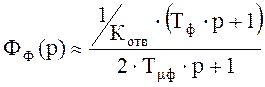
5) Регулятор ЭДС.
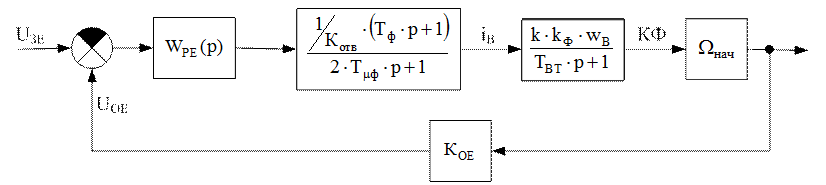
Рис. 7. Контур ЭДС.
Передаточная функция объекта управления Контура ЭДС имеет вид:
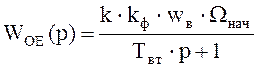 ,
,
Но в передаточной функции замкнутого контура потока имеется форсирующее звено с постоянной времени Тф = Твт. В результате в прямом канале контура получим :
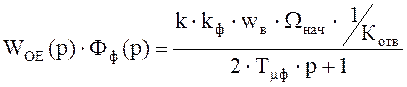 .
.
Т.о.
объект регулирования – безинерчионный и для настройки на ТО необходим
И-регулятор. При это малая постоянная времени контура будет равна: ![]()
Передаточная функция регулятора:
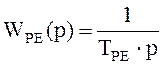 , где
, где
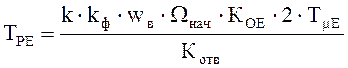
В качестве Ωнач необходимо взять значение, которое даст максимальный коэффициент передачи контура, т.е. Ωнач = ωmax = 23,9 рад/с.
Коэффициент обратной связи по ЭДС:
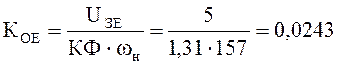
Коэффициент согласования в канале обратной связи по току:
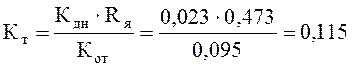
Коэффициент передачи выдилителя модуля:
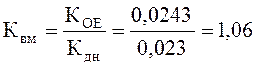
Расчет электрических номиналов элементов регуляторов
1) Регулятор напряжения.
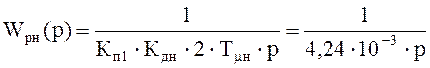
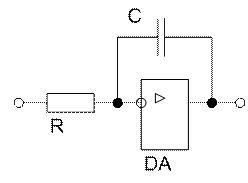
Рис. 8. Электрическая схема регулятора напряжения.
Т = R·C = 4,24·10-3 с.
Принимаем: С = 1,6 мкФ, тогда R = Т/С = 4,24·10-3 / 1,6·10-6 = 2650 Ом.
Принимаем: R = 2,7 кОм.
2) Регулятор тока.
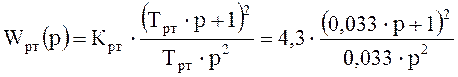
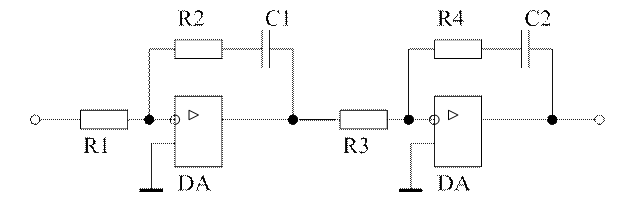
Рис. 9. Электрическая схема регулятора тока.
Т = R2·C1 = R4·C2 = 0,033 c
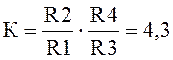
Принимаем: С1 = С2 = 3,3 мкФ; R2 = R4 = Т/С2 = 0,033 / 3,3·10-6 = 10000 Ом
Принимаем: R2 = R4 = 10 кОм, тогда
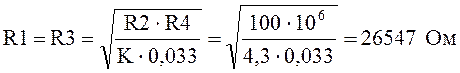
Принимаем: R1 = R3 = 27 кОм
3) Регулятор натяжения.
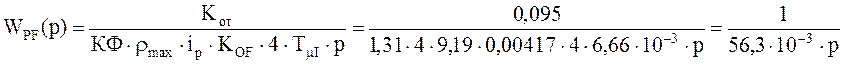

Рис. 10. Электрическая схема регулятора натяжения.
Т = R·C = 56,3·10-3 с.
Принимаем: С = 1,2 мкФ, тогда R = Т/С = 56,3·10-3 / 1,2·10-6 = 46917 Ом.
Принимаем: R = 47 кОм.
4) Регулятор потока.
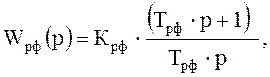
с параметрами:
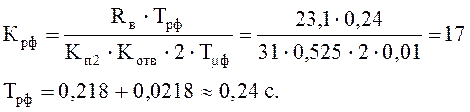
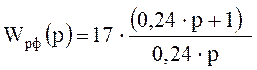
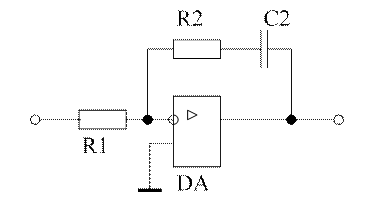
Рис. 11. Электрическая схема регулятора потока.
Т = R2·C2 = 0,24 с,
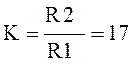 ,
,
Принимаем: С2 = 12 мкФ, тогда R2 = Т/С2 = 0,24 / 12·10-6 = 20000 Ом.
Принимаем: R2 = 20 кОм.
5) Регулятор ЭДС.
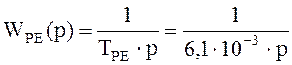 , где
, где
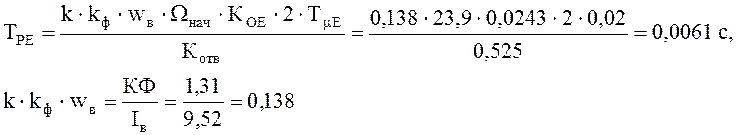

Рис. 12. Электрическая схема регулятора ЭДС.
Т = R·C = 6,1·10-3 с.
Принимаем: С = 1,3 мкФ, тогда R = Т/С = 6,1·10-3 / 1,3·10-6 = 4692 Ом.
Принимаем: R = 4,7 кОм.
6. Анализ динамики ЭП
Анализы динамики системы автоматического управления электроприводом наматывающего устройства заключается в расчетах переходных процессов основных динамических показателей системы.
Расчет переходных процессов произведем в программе Matlab в приложении Simulink.
Построим переходные процессы для натяжения и КФ, причем переходной процесс натяжения состоит из двух этапов: заправка металла с ограничение натяжения 10% от номинального значения и при ограничении скорости намотки 15% от номинального значения.
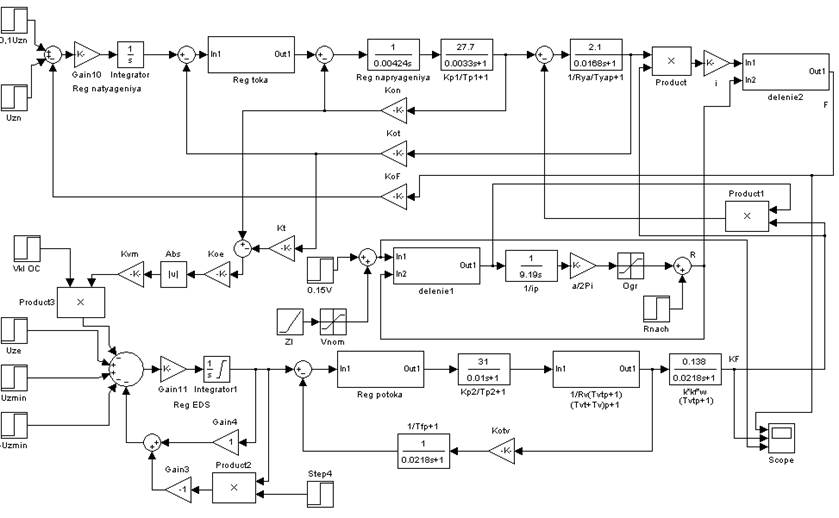
Рис. 13. Фрагмент документа MatLab: структурная схема САУ приводом наматывающего устройства.
Переходные процессы можно рассматривать в несколько этапов.
Сначала задается напряжение задания минимального КФ (оно составляет 2,49 В). Далее при пониженной скорости (15% от рабочего значения) производится заправка материала при ограничении натяжеия 10% от номинального. Далее подается номинальный сигнал задания натяжения (равный 5 В) и линейное нарастание скорости до рабочего значения (6 м/с).
В момент достижения скоростью рабочего значения подается номинальное напряжение задания ЭДС равное 5 В.
Рассмотрим некоторые участки.
1) Скачок напряжения задания минимального потока.
Быстродействие контура ЭДС при синтезе на ТО:
tрегЕ1 = 4,2∙2∙ТμЕ = 4,2·2·0,02 = 0,168 с,
Анализируя переходные процессы видно, что: tрегЕ1 = 0,16 с, т.е. быстродействие контура удовлетворительное.
Перерегулирование:
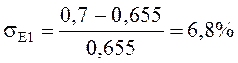
2) Заправка материала при ограничении скорости и натяжения.
Быстродействие контура натяжения:
tрегF1 = 4,2∙2∙ТμF = 4,2·2·0,013 = 0,11 с,
Анализируя переходные процессы видно, что: tрегF1 = 0,1 с.
Перерегулирование в данном случае равно 0.
3) Скачок напряжения задания натяжения до номинального значения и линейное нарастание скорости.
Быстродействие контура натяжения:
tрегF2 = 4,2∙2∙ТμF = 4,2·2·0,013 = 0,11 с,
Анализируя переходные процессы видно, что: tрегF2 = 0,3 с, что больше ожидаемого времени переходного процесса, т.к. данный переходной процесс был получен при скачке номинального напряжения задания.
4) Скачок напряжения задания ЭДС до номинального значения.
Быстродействие контура ЭДС:
tрегЕ2 = 4,2∙2∙ТμЕ = 4,2·2·0,02 = 0,168 с,
Анализируя переходные процессы видно, что: tрегЕ2 = 0,12 с.
Перерегулирование:
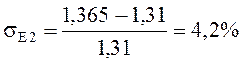
В целом можно сделать вывод, что переходные процессы можно считать
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.