Динамическое программирование. Основные понятия динамического программирования. Принципы динамического программирования

множество управлений (решений), которые могут быть приняты в начале -го года. Множество состоит из двух элементов «сохранение» и «замена»;

 – прибыль в -ом году от использования оборудования;

 – условно-оптимальная прибыль от использования оборудования в период с -го по -й год с принятым решением ;

 – условно-оптимальная прибыль от использования оборудования в период с -го по -й год;

Имеем основное функциональное уравнение 2.1 или в виде 2.2.

                                         (2.1)

                                           (2.2)

Прибыль в -ом году принимает вид 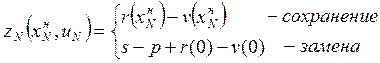2.3.

                         (2.3)

Для -ого планового года имеем 2.4.

                                  (2.4)

Прибыль в -ом году принимает вид 2.5.

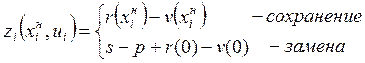                            (2.5)

2.2 Решение задачи о замене оборудования

Так как , что приняли для упрощения задачи, то начнём рассмотрения с последнего 4-го года.

Поясним обозначения:

 – множество состояний (1,2,3,4,5,0) оборудования перед 4-ым годом;

 – множество состояний (1,2,3,4,5,0) после выбора управления в 4-ом году;

 – множество решение (сохранение, замена) в начале 4-ого года.

 – прибыль в 4-ом году от использования оборудования;

 – условно-оптимальная прибыль от использования оборудования в период с 4-го по 5-й год с принятым решением ;

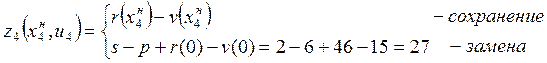
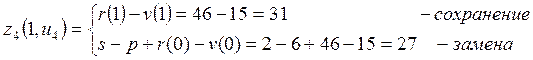
Из последнего видно, что целесообразнее на 4-ом году сохранить оборудование, так как при этом прибыль будет больше, чем при замене (31>27).

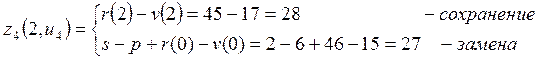
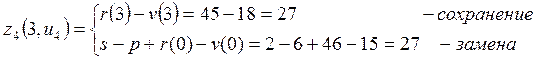
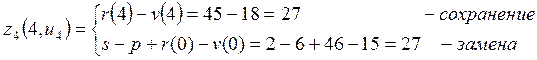
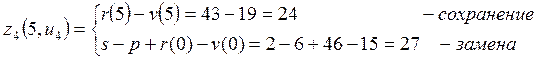
Сведём полученные значения прибылей  и условно-оптимальных прибылей  для 4-ого года использования оборудования с возрастом 1, 2, 3, 4, 5 лет в таблицу 2.2.

Таблица 2.2 – Прибыли в начале 4-ого плавного периода

Перейдем к анализу 3-его года планового периода, записываем функциональное уравнение.

 

       

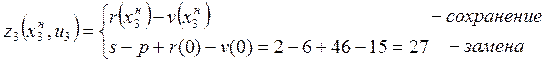
Рассчитаем , :

         

        

        

        

        

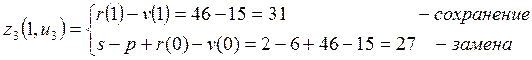
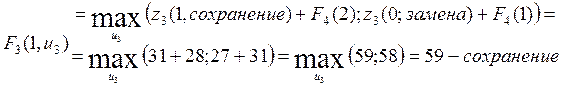
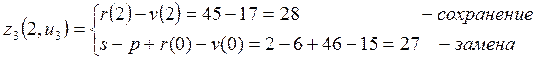
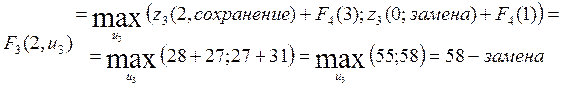
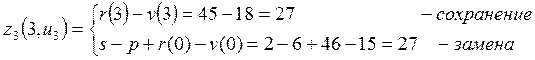
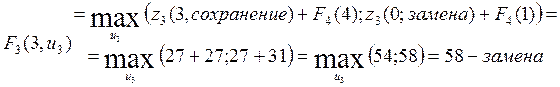
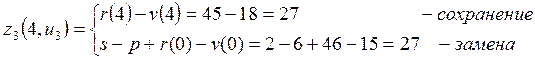
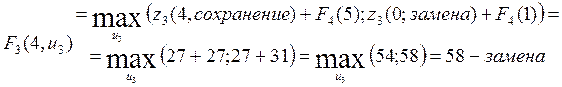
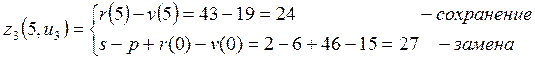
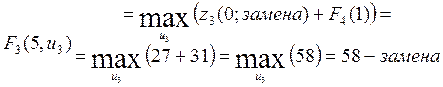
Поясним обозначения:

 – множество состояний оборудования перед -ым годом. Элементами множества могут быть числа , характеризующие возраст оборудования, при чем  – после выбора управления в -ом году и  – в конце -го года;

 – множество управлений (решений), которые могут быть приняты в начале -го года. Множество состоит из двух элементов «сохранение» и «замена»;

 – прибыль в -ом году от использования оборудования;

 – условно-оптимальная прибыль от использования оборудования в период с -го по -й год с принятым решением ;

 – условно-оптимальная прибыль от использования оборудования в период с -го по -й год;

Рассмотрим таблицу 2.3.

Таблица 2.3 – Для пояснений

Из таблицы имеем: во второй строке цифры 1, 2 означают возраст оборудования на начало 3-его года – 1 год, к концу 3-его года – 2 года, т.е. постарело.

В третьей строке цифры 0, 1 означают возраст оборудования на начало 3-его года 0 лет (т.е. после замены), к концу 3-его года – 1 год, т.е. постарело (эксплуатировалось 1 год).

Составим таблицу 2.4 с получением прибыли за 3 и 4 плановые периоды.

Таблица 2.4 – Прибыли за 3,4 плановые периоды

			(из предыдущей таблиц по 1-ой колонке)		(из предыдущей таблицы соответственно )
1	Сохранение	1	2	31	28	59	59
	Замена	0	1	27	31	58
2	Сохранение	2	3	28	27	55	58
	Замена	0	1	27	31	58
3	Сохранение	3	4	27	27	54	58
	Замена	0	1	27	31	58
4	Сохранение	4	5	27	27	54	58
	Замена	0	1	27	31	58
5	Сохранение	5	-	24	-		58
	Замена	0	1	27	31	58

Продолжим вычисления, которые сведем в таблицы 2.5 и 2.6.

Таблица 2.5 – Прибыли со 2-ого по 4-ый плановые периоды

			(из предыдущей таблиц по 1-ой колонке)		(из предыдущей таблицы соответственно )
1	Сохранение	1	2	31	58	89	89
	Замена	0	1	27	59	86
2	Сохранение	2	3	28	58	86	86
	Замена	0	1	27	59	86
3	Сохранение	3	4	27	58	85	86
	Замена	0	1	27	59	86
4	Сохранение	4	5	27	58	85	86
	Замена	0	1	27	59	86
5	Сохранение	5	-	24	-		86
	Замена	0	1	27	59	86

Таблица 2.6 – Прибыли для всего 4-ого периода

			(из предыдущей таблиц по 1-ой колонке)		(из предыдущей таблицы соответственно )
0	Сохранение	0	1	31	89	120	120
1	Сохранение	1	2	31	86	117	117
	Замена	0	1	27	89	116
2	Сохранение	2	3	28	86	114	116
	Замена	0	1	27	89	116
3	Сохранение	3	4	27	86	113	116
	Замена	0	1	27	89	116
4	Сохранение	4	5	27	86	113	116
	Замена	0	1	27	89	116
5	Сохранение	5	-	24			116
	Замена	0	1	27	89	116

Составим таблицу 2.7 максимальных прибылей по предыдущим расчетам.

Таблица 2.7 – Матрица максимальных прибылей

Возраста оборудования, -лет	Годы планового периода
	1-4	2-4	3,4	4
	Максимальная прибыль, ден.ед.
0	120			-
1	117	89	59	31
2	116	86	58	28
3	116	86	58	27
4	116	86	58	27
5	116	86	58	27

Из таблицы 2.7 имеем, все элементы выше жирной линии, находятся в «области сохранения», все элемент ниже жирной линии – в «области замены».

Каждый столбец таблицы 2.7 соответствует столбцам таблиц прибылей .

2.3 Выводы по результатам решения

Из условия задачи п.2.1 пусть на начало планового периода имеется оборудование в возрасте 4-е года. Тогда по таблице максимальных прибылей 2.7 п.2.2 на пересечении  и столбца  находится элемент 116 – максимальная прибыль за четыре года. Этот элемент расположен в зоне замены. Заменив оборудование и использовав его в течение года, к началу третьего второго года окажемся с оборудованием в возрасте 1 год. На пересечении  и столбца  расположен элемент 89 – максимальной прибыли в зоне сохранения. Продолжая политику, как показано на рисунке, к 4-ому году оборудование необходимо сохранить.

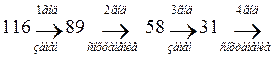
Рисунок 2.1 – Политика использования оборудования

Из условия п.2.1. пусть на начало планового периода имеется оборудование в возрасте 1-о года. Следуя политике, как показано на рисунке, к 4-ому году оборудование необходимо также сохранить.

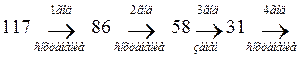
Рисунок 2.2 – Политика использования оборудования

Заключение

В результате курсовой работы для решения поставленной задачи рассмотрены основные понятия и принципы динамического программирования в п.1.1 – п.1.2.

Рассмотрен принцип оптимальности Беллмана в задаче о замене оборудования, который записывается функциональными уравнениями 1.2 – 1.6 рекуррентного характера, которые рассмотрены в п.1.3.

На примере рассмотренной задачи из сборника [1] решена задача