Основные типы функций выпуска. Оценка параметров степенной производственной функции. Параметры множественной линейной функции регрессии линейного вида в MS Excel

Лабораторная работа 7. Основные типы функций выпуска

1. Оценка параметров степенной производственной функции

Рассмотрим двухфакторную производственную функцию Кобба-Дугласа ,  , .  Параметры этой функции  , ,  можно установить  множественным регрессионным анализом, предварительно приведя функцию к линейному виду: .

Параметры множественной линейной функции регрессии линейного вида в MS Excel устанавливаются при помощи функции ЛИНЕЙН. Для ввода результата необходимо выделить матрицу в размере , где  - количество переменных, строк – всегда 5.

Введите диапазоны данных как показано в таблице.

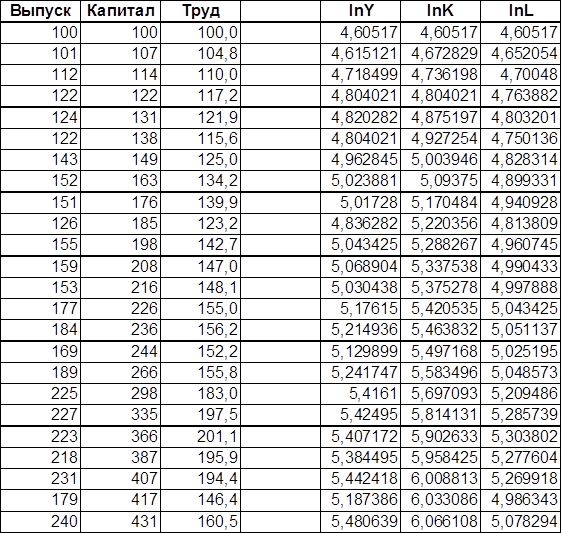
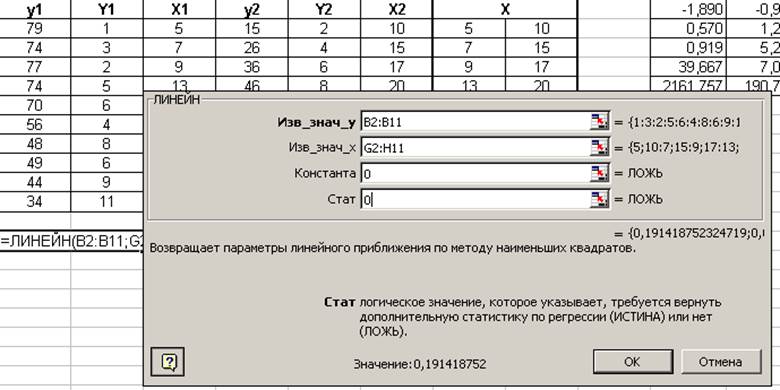
Выделите область ячеек. И введите диапазоны данных, используя функцию ЛИНЕЙН, как показано на рис.1.

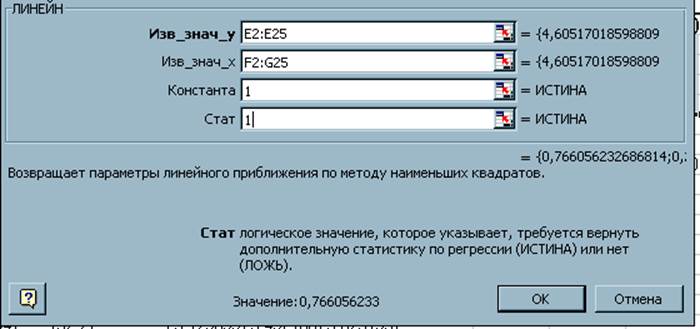
Поскольку функция ЛИНЕЙН матричная, то необходимо помнить, что независимые переменные  вводятся в виде единой матрицы. Ввод константы и статистики обеспечивает представление результатов вычислений в различных  вариантах. Константа обозначает свободный член уравнения. Поэтому если константе присвоить значение "1". То уравнение будет представлено со свободным членом, если "0", то уравнение будет представлено без свободного члена. При назначении статистики "1", будет выведена оценка достоверности, если "0", то нет.  При работе с массивами данных в MS Excel необходимо применять команду с одновременным нажатием клавиш <Shift>+<Ctrl>+<Enter>.

В выводимой функцией ЛИНЕЙН таблице результатов представлены следующие параметры (для функции двух независимых переменных):

расч

, ,  - параметры регрессии; , ,  - стандартные отклонения параметров;  - стандартное отклонение ;  - коэффициент детерминации; _расч - -статистика;  - число степеней свободы, определяемое по формуле , где  - количество исходных данных,  - число переменных;  - регрессионная сумма квадратов;  - остаточная сумма квадратов.

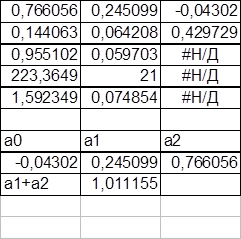
Рис. 2

Как видно, сумма  - неизменный коэффициент масштаба.

2. Использование производственных функций в сравнительном экономическом анализе

Ø Рассчитать сравнительную эффективность двух предприятий.

Ø Построить производственные функции по статистическим данным работы двух предприятий (таблица 2).

Ø Оценить фондоотдачу предприятий согласно статистическим данным, определить сравнительную экономию основных фондов (таблица 2) за все годы работы.

Ø Определить производительность труда на предприятиях и рассчитать сравнительную экономию трудовых ресурсов.

Ø Сделать вывод о том, какое предприятие работает более эффективно.

Ø Составить отчет.

3. Системы одновременных уравнений

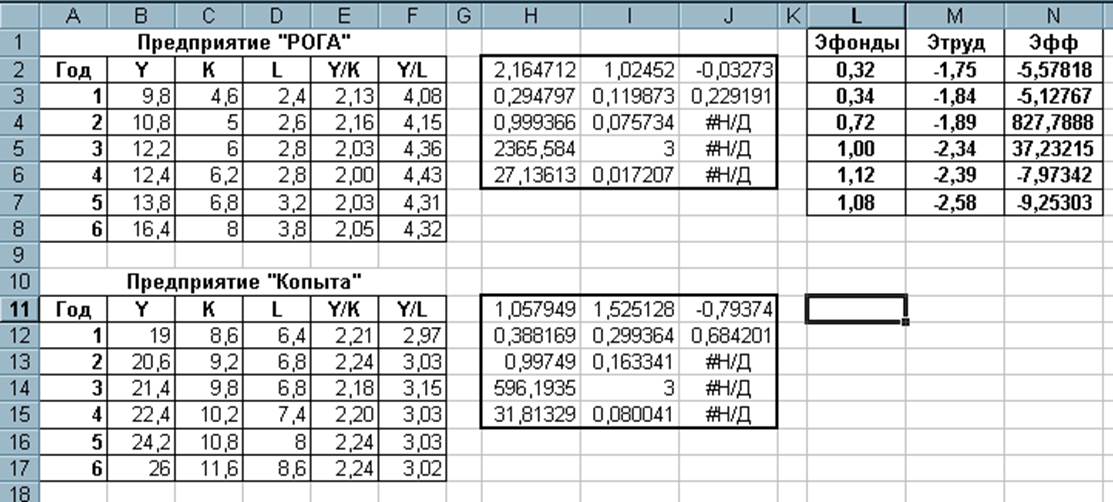
При моделировании достаточно сложных экономических объектов часто приходится вводить не одно, а несколько связанных между собой уравнений. Таким образом, при проведении регрессионного анализа модели может возникнуть необходимость оценивать систему уравнений, что требует введения новых понятий и требований.

Методы оценивания систем одновременных уравнений можно разделить на методы, позволяющие оценивать каждое из уравнений поочередно, и методы, предназначенные для оценивания всех уравнений сразу. Примерами первой группы может служить двухшаговый метод наименьших квадратов и метод ограниченной информации для одного уравнения, а примерами методов второй группы – трехшаговый метод наименьших квадратов и метод максимального правдоподобия полной информации.

В Excel нет встроенного двухшагового метода наименьших квадратов. Поэтому основные возможности следующие: последовательные вычисления с использованием функции ЛИНЕЙН, учитывая, что она выводит вектор-строку коэффициентов регрессии в обратном порядке. Поэтому вектор-столбец коэффициентов при транспонировании также выходит в обратном порядке. Следующая возможность – использовать матричные функции или комбинацию матричных функций и функции ЛИНЕЙН. Рассмотрим систему уравнений «спрос-предложение». Обозначим  - спрос;  - предложение; ,  - цена; ,  - доход, , , , , ,  - искомые коэффициенты регрессий:

Ввести исходные данные как показано в таблице 3.

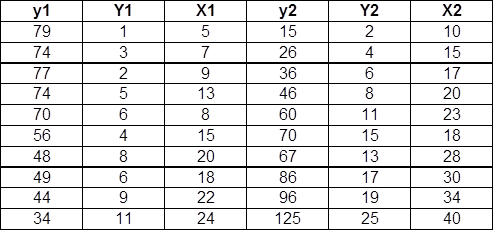Таблица 3

Определить для сравнения коэффициенты уравнений обычным методом наименьших квадратов, т.е. применить функцию ЛИНЕЙН к обоим уравнениям (Табл.4).

Таблица 4

Записать, как выглядят уравнения с найденными коэффициентами.

Использование двухшагового метода наименьших квадратов.

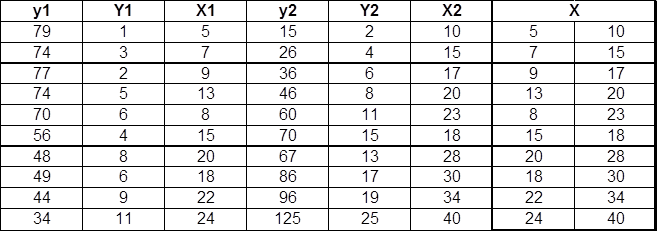
Преобразовать матрицу  как показано в таблице 5

Таблица 5

Определить коэффициенты приведенной формы для первого уравнения. Для этого нужно применить функцию ЛИНЕЙН к  и матрице  и вывести результат, как показано в таблице 5.

Таблица 5

Сформировать вектор коэффициентов приведенной  формы, скопировав значение ячейки А13 в ячейку B14. Рассчитать вектор прогнозных значений  в столбце J2:J11, перемножив матрицу  на вектор коэффициентов приведенной формы. Для этого нужно использовать функцию МУМНОЖ как функцию массива, т.е. ввести ее в диапазон J2:J11 при помощи клавиш <Shift>+<Ctrl>+<Enter>.

Определить коэффициенты регрессии для первого уравнения между  и матрицей , которая сформирована в ячейках J2:K11 (функция ЛИНЕЙН). Ответ ввести в ячейки F13:H17.

Проделать аналогичные вычисления для второго уравнения, ввести коэффициенты приведенной формы в ячейки D13:E14.

В ячейках L2:L11 рассчитать вектор прогнозных значений  (функция МУМНОЖ).

Сформировать матрицу  в ячейках L2:M11 и определить коэффициенты регрессии для второго уравнения между  и матрицей  функцией ЛИНЕЙН, ввести ответ в ячейки I13:K17.

Таблица 6

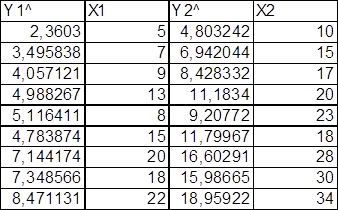
Таблица 7. Коэффициенты регрессии для первого  и второго уравнений

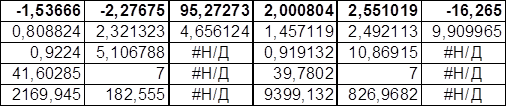
Таким образом, система уравнений выглядит следующим образом:

Оформить отчет.