Двухфакторные производственные функции. Производственная функция Кобба-Дугласа. Предельная норма замены труда капиталом

Лабораторная работа N1. Двухфакторные производственные функции. Часть 1. Производственная функция Кобба-Дугласа.

Производственная функция (ПФ) описывает зависимость объема выпускаемой продукции от затрачиваемых или используемых ресурсов. В данной лабораторной работе мы будем рассматривать двухфакторную производственную функцию Кобба-Дугласа, описывающую зависимость выпуска продукции Q от вложенного капитала K и затраченного труда L в следующем виде

                                                    (1), где A, a, b - положительные параметры; a < 1, b < 1, величина A зависит от выбранных единиц измерения и эффективности производственного процесса.

График ПФ двух переменных, очевидно, представляет собой поверхность в трехмерном пространстве. Линия уровня ПФ, т.е. линия, в каждой точке которой объем выпуска при разных значениях K, L один и тот же, называется изоквантой или кривой безразличия производства. Изокванты не пересекаются, причем большему объему производства отвечают изокванты, более удаленные от начала координат.

При исследовании свойств ПФ используются предельные величины. Предельным продуктом капитала (труда) называется частная производная ПФ по переменной K (L) соответственно:

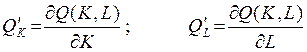     .                       (2)

Легко показать, что предельные продукты капитала и труда для ПФ Кобба-Дугласа равны:

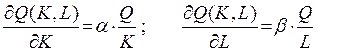.                         (3)

Еще одной важной характеристикой ПФ является предельная норма замены труда капиталом, определяемая отношением соответствующих предельных продуктов и для функции Кобба-Дугласа имеющая вид:

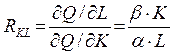 .                                              (4)

            Задание к лабораторной работе

1. Построение графика функции Кобба – Дугласа с помощью Excel

На начальном этапе необходимо задать сетку точек, в которых будет производиться расчет функции. Введите в ячейку A2 значение 0,1. С помощью маркера автозаполнения занесите в ячейки A2:A26 значения переменной K (шаг установите равным 0,2). Аналогично, используя то же начальное значение (0,1) и значение шага, сформируйте сетку точек в ячейках B1:Z1. (Для удобства восприятия уменьшите ширину столбцов A-Z).

Занесите в ячейки A30:C30 значения параметров A, a, b (например 100; 0,3 и 0,7 соответственно).

В ячейку B2 введите расчетную формулу =$A$30*($A2^$B$30)*(B$1^$C$30). Используя маркер автозаполнения скопируйте данную формулу в диапазон B2:Z26.

На основании расчетных значений ПФ Кобба-Дугласа постройте график (Вставка – Диаграмма, выберите тип Поверхность, в списке вид укажите стандартную поверхность. В следующем окне диалога на вкладке Диапазон данных выберите Ряды в столбцах, в поле Диапазон введите A1:Z26).

После построения поверхности вы можете менять ее ориентацию в пространстве. Для этого выделите диаграмму, выполните команду Диаграмма – объемный вид и в диалоговом окне Формат трехмерной проекции найдите и используйте кнопки, осуществляющие поворот диаграммы.

2. Построение изоквант функции Кобба – Дугласа

Скопируйте полученную диаграмму в область по соседству с областью исходной диаграммы (при этом должна быть нажата клавиша Ctrl). Выделите дочернюю диаграмму и выполните последовательность действий Диаграмма – Тип диаграммы. Далее для типа Поверхностная выберите вид Контурная диаграмма. Полученные в результате кривые представляют изокванты ПФ. При желании вы можете изменить расстояние по вертикали (шаг по z) между секущими плоскостями. Для этого щелкните два раза по области легенды и в появившемся окне диалога на вкладке Шкала установите новую цену основных и промежуточных делений (соответствующий флажок должен быть убран). Озаглавьте рабочий лист (например, Функция Кобба-Дугласа). Измените значения параметров a, b и понаблюдайте за изменениями расчетных графиков. Сумма данных постоянных может быть как равна единице, так и быть меньше или больше единицы.

3. Построение поверхностей предельного продукта капитала и труда

Расчет данных функций будем проводить по формулам (3). Вначале рассчитаем предельный продукт капитала.

Скопируйте рабочий лист с рассчитанной функцией Кобба-Дугласа. Для этого достаточно щелкнуть правой кнопкой мыши на ярлычке рабочего листа, выбрать в контекстном меню опцию переместить/скопировать и установить флажок создавать копию. Переименуйте скопированный лист (например, Q_K). Выделите ячейку B2 и измените в формульной строке формулу =$A$30*$B$30*($A2^$B$30)*(B$1^$C$30) на

=$A$30*$B$30*($A2^$B$30)*(B$1^$C$30)/$A2. Используя маркер автозаполнения скопируйте данную формулу в диапазон B2:Z26.

Постройте аналогично предыдущему случаю диаграмму для рассчитанной функции предельного продукта капитала.

Аналогичным образом рассчитайте и представьте в виде диаграммы предельный продукт труда.

Указание: расчет проведите на отдельном листе (используйте копирование рабочего листа). В ячейку B2 необходимо ввести формулу =$A$30*$B$30*($A2^$B$30)*(B$1^$C$30)/B$1 и провести копирование в диапазон B2:Z26. Постройте диаграмму.

4. Построение поверхности предельной нормы замены труда капиталом.

Постройте расчетную сетку точек аналогично предыдущим случаям. В ячейки A30 и B30 введите значения параметров a, b (в нашем случае 0,3 и 0,7). В ячейку B2 введите формулу = ($B$30/$A$30)*($A2/B$1) и скопируйте формулу в диапазон ячеек B2:Z26. Постройте диаграмму.