Изображение синусоиды, ее производной иинтеграла на комплексной плоскости. Индуктивный элемент в цепи синусоидального тока

Токи в ветвях определяют наложением контурных токов, замыкающихся через каждую ветвь. Расчетные уравнения получают по второму закону Кирхгофа, так что система контурных уравнений имеет порядок     р = [n'-(q-1]. Каждая

ветвь с идеальным источником тока снижает порядок системы на 1: n'= n - nj. Система уравнений по МКТ в матричной форме записывается в следующем виде:

       где [Rkk] - матрица контурных сопротивлений, размерностью р х р; р - количество расчетных контурных токов. Например, для системы третьего порядка:

На главной диагонали коэффициенты R11, R22, R33 - сумма сопротивлений первого, второго и третьего контуров, соответственно. Коэффициенты всегда положительные. Остальные коэффициенты с разными индексами Rki- сумма сопротивлений ветвей, общих для контура к и i. Коэффициент положителен, если контурные токи к и iна общем сопротивлении направлены одинаково, и отрицателен, если неодинаково. Матрица симметрична относительно главной диагонали, т.е. Rki= RiK.

       

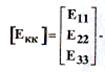  матрица контурных ЭДС: сумма ЭДС данного контура. Правило знаков: если ЭДС ветви совпадает с направлением контура, то «+», и если не совпадает - то «-».

Порядок расчета по МКТ:

1. Определим количество неизвестных контурных токов.

2. Выберем путь протекания тока источника.

3. Составим систему уравнений по МКТ, решим полученную систему уравнений.

4. Определим токи в ветвях, суммируя контурные токи, замыкающиеся через данную ветвь. Правило знаков: если контурный ток замыкается через ветвь и совпадает по направлению с током ветви, то «+»; если не совпадает, то «-».

5. Рассчитаем баланс мощностей.

Метод узловых потенциалов (МУП)

В качестве неизвестных в данном методе выбираются узловые потенциалы, определяемые относительно некоторого базового узла, потенциал которого принимается равным 0. Общее количество неизвестных потенциалов составляет

q =(у -1) и равно числу независимых уравнений по первому закону Кирхгофа. Расчетная система уравнений в матричной форме записывается следующим образом:

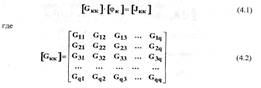
Матрица узловых проводимостей размерностью qxq симметрична относительно главной диагонали. Коэффициенты G11, G22 ... G_qq, лежащие на главной диагонали, всегда положительны, носят название «проводимость к-го узла» и равны сумме проводимостей ветвей, подключенных к узлу к. Коэффициенты, расположенные на боковых диагоналях Gqk, рассчитываются как сумма проводимостей ветвей, соединяющих узел «q» и узел «к». Коэффициенты всегда отрицательны,   и   в   силу симметрии матрицы узловой проводимости

 матрица размерностью q х 1 - столбцовая матрица неизвестных узловых потенциалов;

 столбцовая матрица узловых токов, имеющих в своей сумме члены двух видов:

где ± Ек gK - произведение ЭДС ветви, подключенной к данному узлу на проводимость данной ветви. Знак «плюс» ставится, если ЭДС направлена к узлу, и «минус» - если от узла;

± Jk- ток источников тока, подключенных к данной ветви. Знак «плюс» ставится в том случае, если ток источника направлен к узлу, и «минус», если от узла.

Решая систему уравнений (4.1), определяют узловые потенциалы. Токи в ветвях рассчитывают по закону Ома для активной ветви.

Порядок расчета цепей МУП

1. Прежде чем приступить к формированию уравнений по МУП, рассчитаем полные сопротивления ветвей:

2. Определим количество расчетных уравнений.

Примечание: в схеме имеется один источник тока J. Поскольку внутреннее сопротивление идеального источника тока

Rj = со, то если ветвь с источником тока не содержит последовательно включенных сопротивлений, достаточно показать, к каким узлам схемы подключен источник тока.

3. Сформируем расчетную систему уравнений.

4. Выберем произвольно направления токов в ветвях и рассчитаем их значения по закону Ома.

5. Проверим правильность расчета токов  по первому закону Кирхгофа