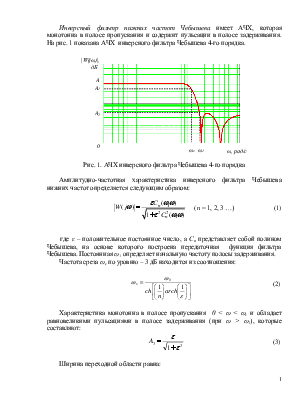
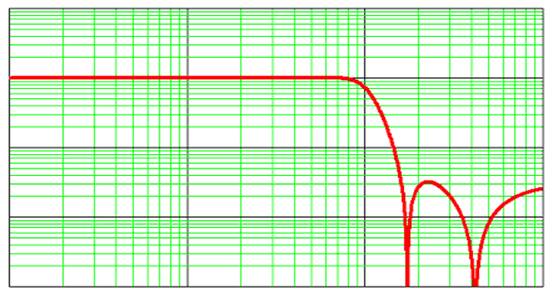
Инверсный фильтр нижних частот Чебышева. АЧХ инверсного фильтра Чебышева 4-го порядка. Биквадратная схема фильтра нижних частот 2-го порядка

Инверсный фильтр нижних частот Чебышеваимеет АЧХ, которая монотонна в полосе пропускания и содержит пульсации в полосе задерживания. На рис. 1 показана АЧХ  инверсного фильтра Чебышева 4-го порядка.

Рис. 1. АЧХ инверсного фильтра Чебышева 4-го порядка

Амплитудно-частотная характеристика инверсного фильтра Чебышева нижних частот определяется следующим образом:

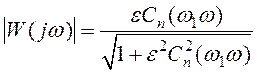                                        (n = 1, 2, 3 …)                        (1)

где ε – положительное постоянное число, а С_n представляет собой полином Чебышева, на основе которого построена передаточная  функция фильтра Чебышева. Постоянная ω₁ определяет начальную частоту полосы задерживания.

Частота среза ω_с по уровню – 3 дБ находится из соотношения:

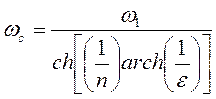                                                 (2)

Характеристика монотонна в полосе пропускания  0 < ω < ω_c и обладает равновеликими пульсациями в полосе задерживания (при ω > ω₁), которые составляют: 

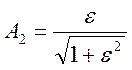                                                     (3)

Ширина переходной области равна:

                                                                                                              (4)

Если  α₂= – 20lgA  представляет собой минимальное затухание в полосе задерживания (дБ), то:

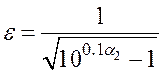                                                                                                      (5) 

Следовательно, для заданного порядка n, минимально допустимого затухания в полосе задерживания α₂ и частоты ω₁ (начала полосы задерживания, содержащей пульсации) можно из (5) найти значение ε, а из (1) – требуемую амплитудно-частотную характеристику. Тогда частоту среза ω_c  и ширину переходной области можно определить из (2) и (4).

Минимальный порядок n, требуемый для обеспечения заданных технических требований по α₂, ω_c и ω₁ из (2) и (5), определяется следующим образом:

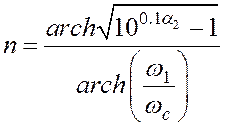                                               (6)

Соотношение между шириной переходной области T_ω  и отношением частот ω₁ / ω_c находится из (4) и равно:

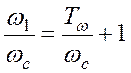                                                    (7)

Из (6) и (7) можно также получить нормированную ширину переходной области:

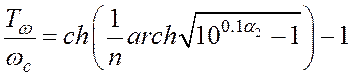                               (8)

Следовательно, для более узкой переходной области требуется большее значение порядка n, что связано с увеличением числа пульсаций. 

Инверсный фильтр Чебышева  является  неполиномиальным фильтром, его передаточная функция имеет общий вид (16). В общем случае инверсный фильтр Чебышева более сложен в реализации, чем полиномиальные фильтры Баттерворта и Чебышева.

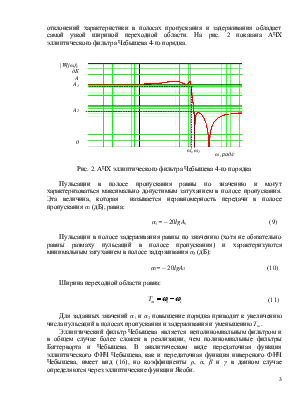
Эллиптический фильтр нижних частот Чебышева (фильтр Кауэра) – имеет амплитудно-частотную характеристику, которая содержит пульсации как в полосе пропускания, так и в полосе задерживания. Данный фильтр является лучшим среди всех классов ФНЧ в том смысле, что для заданного порядка и допустимых отклонений характеристики в полосах пропускания и задерживания обладает самой узкой шириной переходной области. На рис. 2 показана АЧХ эллиптического фильтра Чебышева 4-го порядка.  

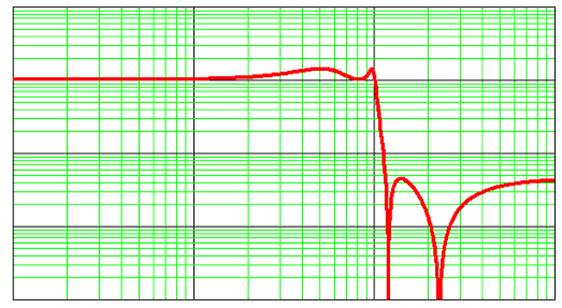
Рис. 2. АЧХ эллиптического фильтра Чебышева 4-го порядка

Пульсации в полосе пропускания равны по значению и могут характеризоваться максимально допустимым затуханием в полосе пропускания. Эта величина, которая  называется неравномерность передачи в полосе пропускания α₁ (дБ), равна:  

α₁= – 20lgA₁(9)

Пульсации в полосе задерживания равны по значению (хотя не обязательно равны размаху пульсаций в полосе пропускания) и характеризуются минимальным затуханием в полосе задерживания α₂ (дБ):

α₂= – 20lgA₂ (10)

Ширина переходной области равна:

                                                                                                              (11)

Для заданных значений α₁ и α₂ повышение порядка приводит к увеличению числа пульсаций в полосах пропускания и задерживания и уменьшению T_ω .

Эллиптический фильтр Чебышева  является  неполиномиальным фильтром и в общем случае более сложен в реализации, чем полиномиальные фильтры Баттерворта и Чебышева. В аналитическом виде передаточная функция эллиптического ФНЧ Чебышева, как и передаточная функция инверсного ФНЧ Чебышева, имеет вид (16), но коэффициенты ρ, α, β и γ в данном случае определяются через эллиптические функции Якоби.

 Биквадратный фильтр нижних частот 2-го порядка. На рис. 3 представлена схема  фильтра нижних частот на основе биквадратной схемы.

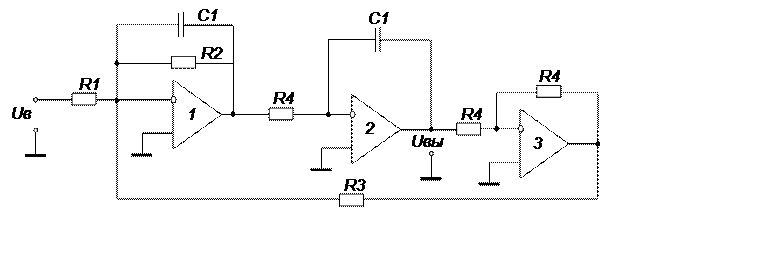Рис. 3. Биквадратная схема фильтра нижних частот 2-го порядка

Передаточная функция схемы рис. 3 имеет вид:

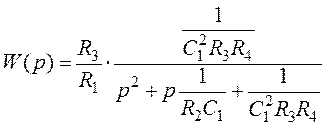                                                                  (12)

ФНЧ на основе биквадратной схемы реализует типовую полиномиальную передаточную функцию звена 2-го порядка с неинвертирующим коэффициентом усиления  k, причем справедливо:

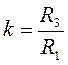
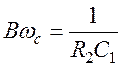                                                        (13)

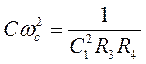
Если задаться значениями емкостей С₁ и резистора R₄, то из данной системы можно найти значения остальных элементов схемы. Значения С₁ и R₄ выбираются из условий:

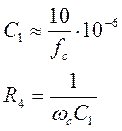                                                              (14)

В этом случае получаем:

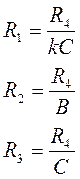                                                                   (15)

Из полученной системы видно, что биквадратная схема относительно легко настраивается. Для выбранных значений С₁ и R₄ изменение R₂ приводит к изменению коэффициента В, изменение R₃ – к изменению коэффициента С, а изменение R₁– к изменению коэффициента усиления k.

2.  Лабораторный стенд для исследования активного фильтра нижних частот