Исследование алгоритма защиты информации RSA. Криптосистемы с открытым ключом. Алгоритм Евклида, страница 2

не мог бы послать шифрованное сообщение или подтвердить подпись Протокол подтверждения подлинности отправителя сообщения.

•  Отправитель А и получатель В знают число р и случайное число N из интервала (1,N). А генерирует случайные числа * и у из того же интервала.

•  х является секретным ключом, а у должно быть взаимно простым с

передает В документ с подписью (Q,R,S,T). в    Получатель    В    проверяет    подпись,    контролируя    тождество

В этой системе секретным ключом для подписания сообщений является число х, а открытым ключом для проверки достоверности подписи - число

Q.

2.2. Криптосистема RSA

В 1978 году R.L.Rivest, A.Shamir, L.Adleman опубликовали криптосистему с открытом ключом, которая стала известной как RSA система. Рассматриваемая система криптографии основывается на следующей теореме.

Теорема (Эйлера). Пусть а и п целые числа. Тогда

где НОД (а, п) - наибольший общий делитель чисел а и п, ф{_п) - функция Эйлера

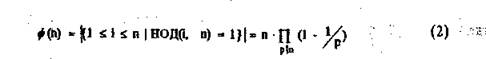
определяется для всех целых положительных о и представляет собой число чисел ряда 0,1,..., п-1 взаимно простых с п. Если существует каноническое разложение числа п

Алгоритм. RSAКаждый пользователь выбирает два простых числа р_и и Яи, произведение которых образует число n_u= p„ q„,. Из (2) следует, что

Далее пользователь U определяет целое число е, 1< е_и<ф(п„) , для которого НОД(е„, ф(п_и)) = 1. С Помощью алгоритма Евклида пользователь U вычисляет за 2log]$(n_u) шагов целое число d_u, удовлетворяющее сравнению

Пользователь U публикует числа е_ц и п„в открытой книге, но держит d„ в секрете. Числа р_и и q_u не играют большой роли, но также не публикуются.

Шифрование сообщения. Если пользователь А хочет передать сообщение m пользователю В (0 < гп < пв), то А выбирает из открытой книги число е_в и вычисляет зашифрованный текст:

С ш m '» modn_a .(5)

Расшифровка сообщения. Пользователь В восстанавливает сообщение m

ИЗ С, ВЫЧИСЛЯЯ

V => C^d» =ш''■*» = m^H1#?n»⁾« m  mod n_B ;      (I-любое)   ,

7

гдеН0Д(т,п_в)=1.

Прииер L Пусть p=2U, q -223, n = pq = 47053, ф(п)= (p-l)(q-l)=46620, открытый ключ е= 16813, секретный ключ d=19837. Пользователь хочет передать английский текст RSA. Буквам соответствуют следующие номера их положения в английском алфавите: R=18, S=19, A=l. Тогда 5- битовое представление текста будет иметь следующий вид:

т=((1-32)+19)32+18=1650.

После шифрования получаем

С =. m^dmo«l n - 1650¹⁶⁸¹³mod 47053 - 3071.

Получатель расшифровывает сообщение с помощью секретного ключа: P^Cmodn = 307l"⁸³⁷mod 47053 = 1650.

Пример 2. Рассмотрим случай, когда используется N- значный алфавит и известны положительные числа к и 1, к<1, причем значения N^k и N¹ охватывают диапазон около 200 значного числа. Используется английский алфавит из N=26 букв, к=3,1=4. Шифруемое слово "YES".

формирование ключей пользователя А

1.  Определяется величина модуля  N^k< n_A <Я\ Для этого выбираются простые числа p_A=281,q_A= 167, п_А= p_Aq_A = 281167 =46927.

2.  Используя генератор случайных чисел определяется секретный ключ е_А= 39423, удовлетворяющий условиям НОД(е_А, р_А-1) = НОД(е_А, q_A-3.   Вычисляется открытый ключ d_л = е'2 mod( р_л - Щйл " ^l) ⁼ 26767 4   Числар_А, q_A, d_A являются секретными.

Пользователь А использует для шифрования ключ (п_А, е_А) •*( 46927, 39423). Сообщение представляется в цифровом виде как триграф следующим образом: