Перед расчетом принципиальной схемы каждого блока следует провести анализ осуществляемого схемой принципа обработки сигналов. Конечной целью анализа должно стать определение необходимых зависимостей параметров элементов схемы (номинальных значений сопротивлений и емкостей, основных параметров интегральных усилителей и т. п.) от реализуемой этой схемой функции (генерация, усиление, ограничение и т. д.) и качеством ее выполнения (точность, быстродействие, стабильность). Например, анализ схемы генератора гармонических колебаний должен привести к определению того, при каких условиях возможно существование колебаний и как эти условия реализуются в рассматриваемой схеме, от чего зависит значение частоты этих колебаний, а также к выводу связи качества формируемого сигнала, т. е. степени его приближения к синусоидальному, с соответствующими параметрами схемы. Полученные в результате анализа формулы должны позволить выбрать номиналы элементов схемы, обеспечивающие работу генератора на заданной частоте и с заданным качеством.
ПРИМЕР
ЗАДАНИЕ
Таблица исходных данных примера
|
№ |
Г |
Кн |
f |
DT |
dк |
Iвх |
Uвп |
Uвк |
Uпо |
Rвх |
j |
ФЧВ |
tу1 |
tу2 |
ПНТ |
|
чет |
Т |
1.5 |
50 |
40 |
0.5 |
100 |
0-100 |
50 |
5 |
800 |
60 |
2ВХ |
0.5 |
0.2 |
ПОС |
1.ГЕНЕРАТОР ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Общий порядок проведения анализа схем RC-автогенераторов
1.Выделить из анализируемой типовой схемы RC-автогенератора схему активной частотно-избирательной цепи (ЧИЦ) и составить для нее структурную схему.
2.Записать выражение коэффициента передачи ЧИЦ.
3.Определить частоту настройки ЧИЦ, для чего:
- в соответствии с операторным методом расчета электронных схем записать передаточную функцию W(p) цепи;
- после перехода к комплексному коэффициенту передачи W(jw) вывести выражение для определения частоты настройки w0 ЧИЦ.
4.Определить добротность цепи, для чего:
- записать выражение комплексного коэффициента передачи по относительной частоте W(jx) и перейти к комплексному коэффициенту передачи по относительной расстройке W(jd);
- после определения нормированного коэффициента передачи по относительной расстройке вывести выражение для определения добротности.
5.Провести анализ на выполнение условия баланса амплитуд, для чего: вывести соотношение, связывающее коэффициент передачи ЧИЦ на частоте настройки с параметрами схемы.
6.Провести анализ влияния “ухода” элементов на АЧХ частотно-избирательного усилителя.
7.По результатам п.3¸6 провести расчет и выбор элементов.
Ниже в качестве примера анализа и расчета типовой схемы генератора ИППН приводится рассмотрение схемы RC-генератора на основе одинарного Т-моста (выбор элементов в примере не рассматривается).
Анализ и расчет схемы RC-автогенератора на основе одинарного Т-моста
1.Для ЧИЦ RC-генератора (рис.2.1, рис.2.2) можно записать следующие соотношения
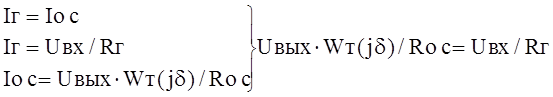 Þ
Þ
Þ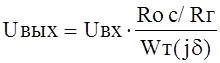
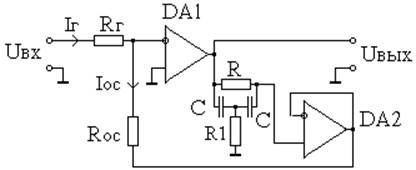
Рис.2.1 Схема активной ЧИЦ
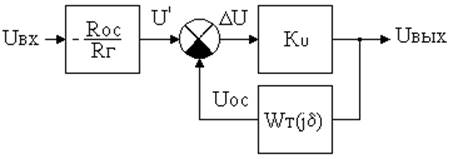
Рис.2.2 Структурная схема активной ЧИЦ
2.Из выражения
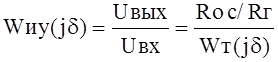
видно, что частотные свойства избирательного усилителя задаются частотно-избирательной цепью на Т-мосте, анализ которой и следует проводить далее.
3.Определение частоты настройки Т-моста (частоты колебаний RC-генератора).
Передаточная функция для Т-моста:
![]()
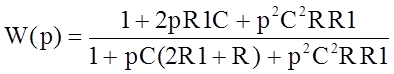
Комплексный коэффициент передачи Т-моста:
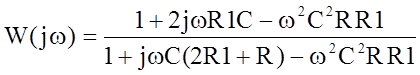
На частоте настройки Т-моста модуль комплексного коэффициента передачи имеет экстремум, а ФЧХ проходит через ноль, т. е. j(w0)=0. Поэтому для определения w0 необходимо выделить из W(jw) мнимую часть
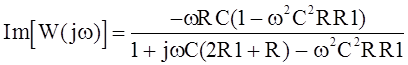
и разрешить относительно w уравнение, полученное приравниванием к нулю числителя
![]()
Откуда
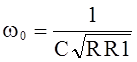
Взяв за постоянную времени Т-моста Т=RC, после преобразований
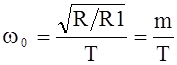 (1)
(1)
4.Определение добротности Q.
Комплексный коэффициент передачи по относительной частоте x=w0/w:
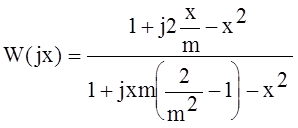
Комплексный коэффициент передачи по относительной расстройке d=x-1/x:
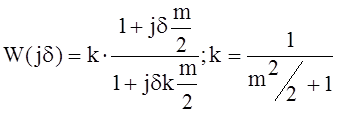
Нормированный коэффициент передачи:
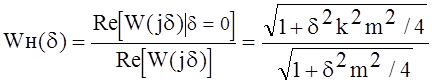
Значение Wн(d) при относительной расстройке по уровню 0.7:
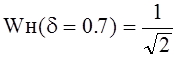
После разрешения уравнения
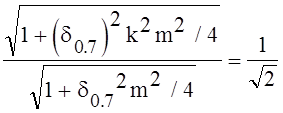
относительно d0.7
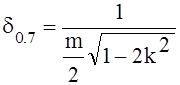
Поскольку добротность является величиной, обратной d0.7, то
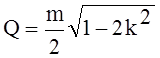
Так как при средних значениях добротности k<<1, то можно считать
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.