Коэффициент затухания волны основного типа в линии передачи с воздушным заполнением. Электрический ток сосредоточен на тонком проводнике, страница 2

Литература: 1, стр. 133 – 161, 165 – 176, 199 – 205.

З а д а ч а 2. Для сопротивлений нагрузки Z_H = W, 0, ∞ и jW/2 рассчитать распределения модуля напряжения вдоль линии передачи (задача 2), считая её  идеальной (не имеющей потерь). Амплитуда падающей волны на входе линии 1В. Для каждой нагрузки рассчитать коэффициент отражения, коэффициент бегущей волны, коэффициент стоячей волны в линии, а также мощность в нагрузке. W – характеристическое сопротивление линии передачи.

Построить рассчитанные распределения напряжения.

Литература: 4, стр. 29 – 42; 5, стр. 119 – 129.

З а д а ч а 3. Показать, что если электрический ток сосредоточен на тонком проводнике, ориентированном вдоль оси Z, то диаграмма направленности проводника имеет вид:

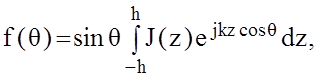
где θ отсчитывается от оси Z,  J(z) –распределение тока, 2h – длина проводника, k = 2π/λ – волновое число, λ – длина волны.

Вычислить диаграмму направленности проводника для следующего распределения тока:

Для n = 6,7 и 8   h = λ/4, для остальных n  h = λ(m+1)/4.

Расчет диаграммы направленности рекомендуется выполнить на компьютере. Определить параметры диаграммы направленности: ширину главного лепестка по нулям и половинной мощности, уровень боковых лепестков. Изобразить графически токовое распределение и форму полученной диаграммы направленности.

Литература: 1, стр.5 – 40, 56 – 70; 4, стр. 222 – 232.

З а д а ч а 4. Рассчитать множитель направленности круглого непрерыв-ного раскрыва радиуса а с амплитудным распределением

Е(r) = (1 – Δ) + Δ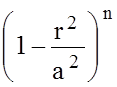

и синфазным фазовым распределением. Радиус раскрыва равен а = 5λ (m +1), где λ – длина волны, Δ = 1/(m +1). Построить множитель направленности в прямоугольной и полярной системах координат.

Рассчитать ширину диаграммы направленности по нулям и половинной мощности, уровень боковых лепестков и коэффициент направленного действия раскрыва.

Литература: 3, стр. 41 – 45, 292 – 310.

З а д а ч а 5. Рассчитать диаграмму направленности в вертикальной плоскости элементарного электрического вибратора, расположенного над плоской однородной землей. Частота колебаний 30ּ  МГц. Высота расположения вибратора h и параметры земли приведены в таблице.

Для нечетных n диаграмму направленности считать в экваториальной плоскости вибратора, λ – длина волны электромагнитных колебаний, ε΄ –  относительная диэлектрическая проницаемость земли, σ – удельная электрическая проводимость земли.

Литература:1, стр.224 – 230, 236 – 241, 308 – 312.