Микропроцессорная система, контроллер, микроконтроллер. Принципы построения микропроцессорных систем. Способы подключения логических элементов к шинам МПС

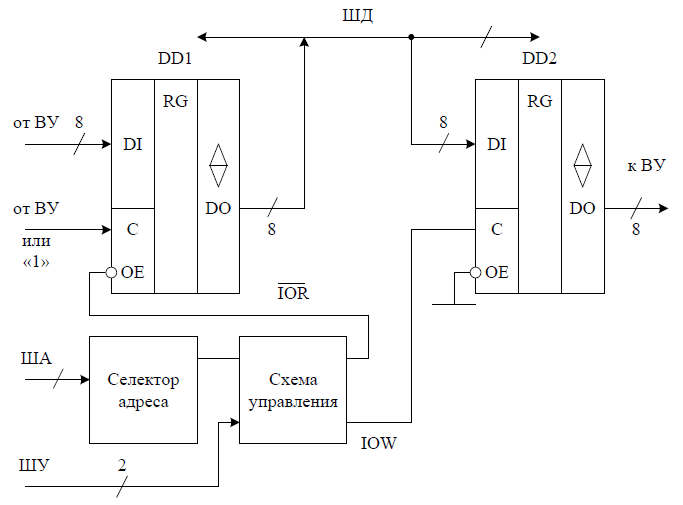
Поэтому разнообразие устройств ввода/вывода неизмеримо больше, чем моду-лей памяти. Объединяют все устройства ввода/вывода общие принци-пы обмена с магистралью и, следовательно, общие принципы органи-зации узлов, осуществляющих сопряжение с магистралью. Как и в случае модуля памяти, они обязательно содержат схему селектора ад-реса, схему управления для обработки стробов обмена и буферы дан-ных. Самые простые устройства ввода/вывода выдают на внешнее устройство код данных в параллельном формате и принимают из внешнего устройства код данных также в параллельном формате. Такие устройства ввода/вывода часто называют параллельными портами ввода/вывода. Они наиболее универсальны, так как способны рабо-тать с большим числом внешних устройств. Поэтому они обычно входят в состав МПС как стандартные устройства. Параллельные порты также всегда имеются в микроконтроллерах.

8. Форматы обрабатываемых данных в МП: двоичные целые числа без знака и со знаком, дробные числа c фиксированной и плавающей точкой, десятичные числа.

В микропроцессорах для кодирования чисел используется дво- ичная система счисления. Практически двоичные числа используются определенной разрядности: 8-разрядное число – это байт, 16- разрядное – слово, 32-разрядное – двойное слово. Применяются две формы представления чисел в двоичном коде: с фиксированной и плавающей точкой.

Числа с фиксированной точкой. В них позиция, в которой точка (запятая) фиксируется между разрядами числа, отделяя целую часть от дробной и определяя вес соответствующих разрядов, посто- янна в процессе вычислений для всего множества используемых чи- сел. Практически используются два положения точки:

1) точка фиксируется после младшего разряда числа. Такие числа принято называть целыми;

2) точка фиксируется перед старшим разрядом числа. Такие числа называются дробными.

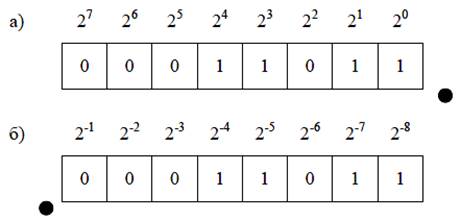
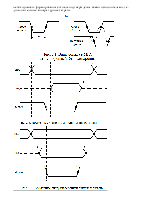
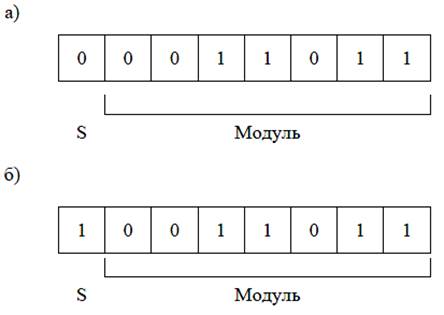
Рис.2.12. Форматы однобайтных беззнаковых двоичных чисел с фиксированной точкой: а) – целые числа; б) – дробные числа

В принципе возможно размещение фиксирующей точки и между разрядами двоичного числа. В этом случае получаются смешанные числа, содержащие целую и дробную части.

Для кодирования двоичных чисел со знаком применяются три вида кодов:

 прямой код;  обратный код;  дополнительный код.

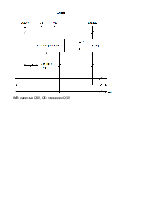
В прямом коде цифровая часть положительных и отрицательных чисел содержит всегда абсолютную величину числа, т.е. его модуль. Этот способ кодирования иногда называют видом знак-модуль. На рис. 2.13 приведены форматы прямых кодов двоичных целых чисел: положительного 11011 и отрицательного -11011. При размещении числа в разрядной сетке свободные старшие разряды цифровой части числа заполняются нулями.

Прямой код однобайтного целого двоичного числа: а) – положительное; б) – отрицательное

Достоинством прямого кода является легкость его получения. Недостатки Обработка чисел, представлен- ных в прямом коде, требует отдельных операций над цифровой и знаковой частями, разных правил выполнения операций сложения и вычитания, приводит к появлению двух представлений нуля: +0 и -0.

Для получения обратного кода отрицательного числа необходи- мо поразрядно инвертировать цифровую его часть, т.е. модуль. Об- ратный код положительного числа совпадает с его прямым кодом.

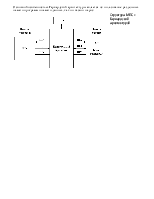
Обратный код однобайтного целого числа: а) – положительное; б) – отрицательное

Достоинством такого метода кодирования являются простота получения обратного кода и возможность выполнения операций сло- жения и вычитания по одним правилам (вычитание заменяется сло- жением уменьшаемого с обратным кодом вычитаемого). Недостаток такой же как в предыдущ.

Для получения дополнительного кода отрицательного числа необходимо поразрядно инвертировать цифровую его часть и приба- вить единицу к результату. Дополнительный код положительного числа совпадает с его прямым кодом.

Достоинством дополнительного кода заключается в том, что во- первых, арифметические операции вычитания и сложения чисел в до- полнительных кодах сводятся к операции алгебраического суммиро- вания, во-вторых, обработка знаковой и циф- ровой частей чисел при сложении производится по одним и тем же правилам, причем правильный знак результата формируется автома- тически; и в-третьих, в дополнительном коде в отличие от прямого и обратного кодов существует единственное представление нуля.

При кодировании дробных двоичных чисел со знаком также вы- деляется