Электромагнитная волна в кольцевом волноводе. Распространение электромагнитных волн в волноводных системах

Следует подчеркнуть, что указанных условий недостаточно для выделения резонансных членов: необходимо еще, чтобы собственные частоты колебаний не перекрывались, т. е. чтобы ω_s была достаточно далека от всех других собственных частот. Оставшиеся в (3.7) после выделения резонансных членов слагаемые будут давать лишь динамические поправки к полю пространственного заряда.

Интересно заметить, что формулы возбуждения открытых резонаторов (колебательные системы, которые имеют достаточно высокую добротность и колебания в которых сопровождаются излучением в свободное пространство)  заданными токами [25] имеют много общего с соотношениями (3.7) — (3.10). Действительно, если открытый резонатор возбуждается сторонними электрическими и магнитными токами с плотностями j^e и j^m соответственно (токи колеблются с частотой ω=ck и находятся на конечных расстояниях), то возбуждаемые ими поля в пренебрежении нерезонансными членами могут быть представлены в виде [25]:

(3.11)

(3.12)

где E_s и H_s-векторные функции удовлетворяющие однородным уравнениям Максвелла (собственные функции)

(3.13)

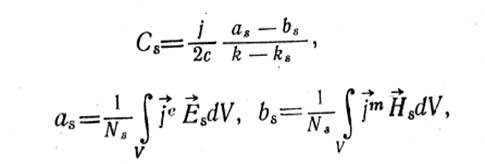                            (3.14)

где

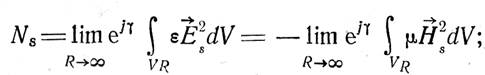
V_R- объем шара радиуса R; γ выбирается так, чтобы интегралы сходились[25].

При построении теории резонансных электронных приборов СВЧ чаще всего в (3.7) и (3.8) достаточно ограничиться рассмотрением одного типа колебаний (основную роль играет резонансный член с одним номером s). Тогда слагаемые с другими номерами s, а также члены с C_-s и (—grad Ф) составляют некоторый нерезонансный фон, который накладывается на данное резонансное s-e колебание. В отличие от возбуждения объемных резонаторов, когда практически всегда в (3.7) и (3.8) можно выделить резонансный член, в случае открытых резонаторов может оказаться, что анализируемая система либо вообще, либо при определенном расположении возбуждающих источников или точки наблюдения не имеет резонансных свойств [25]. Тогда формулы (3.11) — (3.14) не имеют смысла и возбужденные поля описываются формулами (67.19), приведенными [25].

При исследовании квантовых приборов, в частности при описании оптических квантовых генераторов (лазеров), часто оказывается недостаточным ограничиться рассмотрением только одного резонансного члена в формулах возбуждения (3.11) и (3.12), так как эти приборы работают в многомодовом режиме [26, 25]. Так, если спектр собственных частот оказывается достаточно густым, может иметь место взаимодействие типов колебаний даже при очень слабом возмущении полей в колебательной системе. Иными словами, под действием возмущения изменяются собственные функции резонатора: теперь они представляют собой линейную комбинацию нескольких собственных функций первоначальной системы [см. [25], (3.11) и (3.12)].

В вакуумной электронике многомодовость имеет место, например, в приборах типа МЦР, в которых используются открытые резонаторы.

Если теперь считать, что j^e(t) —не первая гармоника плотности тока, а полная плотность сгруппированного в электронном пучке тока (j^e(t)—периодическая функция времени, но не монохроматическая величина), то очевидно, что для амплитуды первой гармоники плотности тока имеет место соотношение

           (3.15)

В работе [26] для идеального резонатора (E*_s — E_s, N*_s= N_s>0) с учетом (3.15) показано, что соотношения (3.9) и (3.10) можно после простых преобразований привести к виду:

(3.16)

(3.17)

где W=1/2 |C_s|²N_s — запас электромагнитной энергии в резонаторе; Р_ea и Р_er - активная и реактивная составляющие электронной мощности взаимодействия     соответственно;

E(t)= Re{C_sE_se^jωt}.

Как нетрудно видеть, выражение (3.16) представляет собой закон сохранения энергии, так как в левой части равенства стоит средняя активная мощность Р_нк = 2ω’’_sW, которая выделяется в нагрузке и теряется в стенках резонатора, а в правой части — средняя за период колебаний активная электронная мощность взаимодействия Р_еа, взятая с обратным знаком. Соотношение (3.16) позволяет, в частности, рассчитать пусковой ток генератора резонансного типа и его   выходную   мощность.

Равенство (3.17) представляет собой баланс реактивных мощностей и позволяет рассчитать частоту генерируемых колебаний. Если поделить (3.17) на (3.16), то получим

(3.18)

Уравнение (3.18) было использовано Л. А. Вайнштейном для исследования стабильности частоты в генераторах магнетронного типа. Оно может быть использовано также для описания явления электронной настройки в отражательном клистроне.

В ряде случаев, например, когда j^е(t) — медленно меняющаяся функция времени, коэффициенты A_s и В_s также становятся медленно меняющимися функциями времени и удовлетворяют уравнениям

(3.19)

В теории большинства электронных приборов СВЧ обычно достаточно использовать лишь первое уравнение системы (3.19), которое с учетом потерь в резонаторе при сравнительно большой добротности Q_s(Q_s>>1) можно переписать в виде      

(3.20)

Уравнение  (3.20)  легко обобщить на случай возбуждения   резонатора   молекулярной