Последовательный колебательный контур. Резонанс напряжений. Внутреннее сопротивление источника ЭДС

1.39) Последовательный колебательный контур. Резонанс напряжений

Последовательным колебательным контуром называют такую цепь, в которой катушка и конденсатор соединены последовательно относительно входных зажимов (рисунок 30). В такой цепи можно наблюдать резонанс напряжений. При резонансе напряжений индуктивное и емкостное сопротивления взаимно компенсируются и в результате этого реактивные сопротивление и мощность цепи равны нулю.

При резонансе напряжений, возникающем в цепи с последовательным соединением индуктивных и емкостных элементов, ток и напряжение цепи совпадают по фазе. В этом случае угол сдвига фаз между током и напряжением равен нулю (φ = 0) и полное сопротивление цепи равно ее активному сопротивлению. Если  то угол φ=0 при Х=0. Следовательно, при резонансе  и  или , откуда угловая частота при резонансе  и резонансная частота .

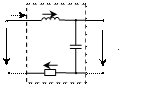
исунок 30

Таким образом, условием возникновения резонанса напряжения в цепи является равенство реактивных сопротивлений Х_L= Х_С, так как в этом случае частота колебательного контура ω₀ равна частоте сети, питающей данную цепь.

Мгновенные значения  энергии магнитного и электрического поля соответственно запишутся

Т.е. в электрической цепи происходит непрерывное перераспределение энергии магнитного и электрического полей, суммарное значение которой постоянно. Вся энергия поступающая от источника в момент резонанса расходуется в сопротивлении R.

Отношение напряжения на индуктивности или емкости к напряжению, приложенному к цепи при резонансе, называют добротностью контура или коэффициентом резонанса.

где  - характеристическое (волновое) сопротивление контура.

Относительной расстройкой частоты по отношению к резонансной частоте контура называют величину: .

Величину обратную добротности называют коэффициентом затухания контура:                                                            .

Полное сопротивление цепи минимально при резонансе напряжений, при этом ток в цепи достигает максимального значения.

Полосу частот вблизи резонанса (рисунок 31), на границах которой ток снижается до максимального значения I₀ принято называть полосой пропускания резонансного контура ,_,  гдеf₁ ,  f₂ – нижняя и верхняя граничная частота.        

Величина добротности Q характеризует остроту резонансной кривой (рисунок 32).

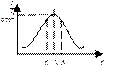
Рисунок 31                                          Рисунок 32

Внутреннее сопротивление источника ЭДС R_iвлияет на добротность и полосу пропускания колебательного контура. Чем больше R_i тем ниже добротность и шире полоса пропускания.

В условиях близких к резонансу, U_L и U_C могут быть велики.

Векторная диаграмма тока и напряжения при резонансе напряжений представлена на рисунке 33.                                      

Зависимость напряжений на емкости и индуктивности от частоты при резонансе напряжений показана на рисунке 34, где U₀ – напряжение при резонансе.

Рисунок 33                     Рисунок 34

2.40) Параллельный колебательный контур. Резонанс токов

Рассмотрим параллельный колебательный контур, простейшим  видом которого является параллельное соединение индуктивной катушки и конденсатора (рисунок 35).

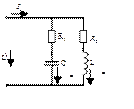
Рисунок 35

Резонансом токов называют такой режим параллельного колебательного контура, при котором ток в неразветвленной части цепи совпадает по фазе с напряжением (φ=0), а мощность, потребляемая из сети, равна активной мощности контура. Реактивная мощность при резонансе из сети не потребляется. 

При резонансе токов . При резонансе токов возможны ситуации, когда реактивные токи  и  намного превышают суммарный ток суммарный ток в цепи, в следствие чего резонанс при параллельном соединении называют резонансом токов. Это возможно при условии g< b_L  или g< b_C.

Определим резонансную частоту контура:

.

После преобразования получаем                              

, откуда  , где ; .

Как видно из выражения для резонансной частоты w_r, резонанс токов возможен при одновременном выполнении условий r>R₁, r>R₂ или r<R₁ и r<R ₂. Если эти условия не выполняются, то w_r - линейное число. В случае, когда R₁ = R₂  w_r  =  w_о при R₁ = R₂ = r; w_r = 0/0, т.е. резонанс токов наступает при любой частоте источника.

Следовательно, ток  в неразветвленной части цепи не зависит от частоты. Если R₁ и R₂ - сопротивления, учитывающие потери реальных конденсаторов и индуктивной катушки (R₁ = R_С ; R₂ = R_L), то как правило, r>>R₁, r>>R₂ при этом  w_r  w_о.

В контуре без потерь (R₁ = R₂ = 0), , токи I_L и I_C  равны по величине