Вопрос 12. Надежность человека-оператора в информационных системах.
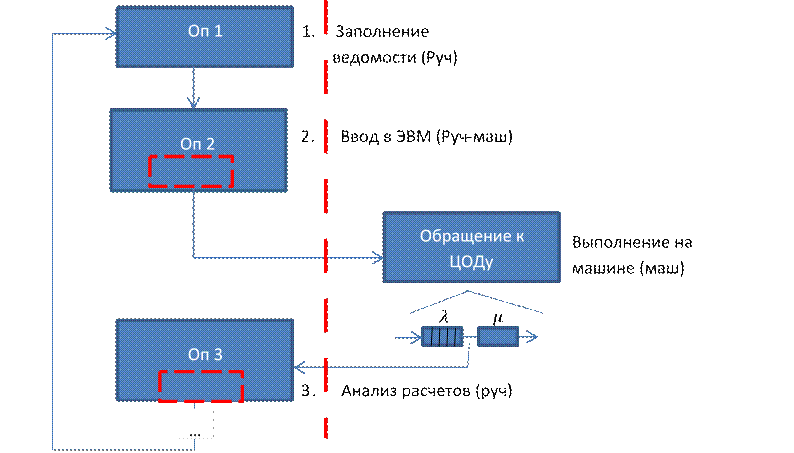
Замечание 1. Человек в контуре управления – часть технологического процесса. Несколько операций.
Замечание 2. Человека моделируем как прибор в системе M/M/1. Под надежностью понимается загрузка прибора (системы?). Работа человека оператора моделируется сетью массового обслуживания.
Замечание 3. Критическим значением, которое не
должно превышаться ![]() не больше 0,75.
не больше 0,75.
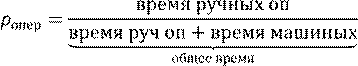
![]() – кол-во символов/скорость печати
– кол-во символов/скорость печати
Моделируем каждую операцию системой М/М/1. Имеем СеМО – замкнутая (источника заявок нет). Метод решения – сводим к разомкнутой, для которой все вычисления просты.
Задержки в каждом узле умноженное на коэффициент передачи.
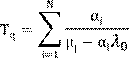
Чтобы сократить задержки – автоматизировать (если экономически эффективно) некоторые ручные операции.
Метод решения:
1. Замкнутую сеть неким образом преобразуем в разомкнутую. Разделяем машинные и ручные операции. Слева замкнутая сеть с 1 заявкой. Справа – разомкнутая сеть.
2.
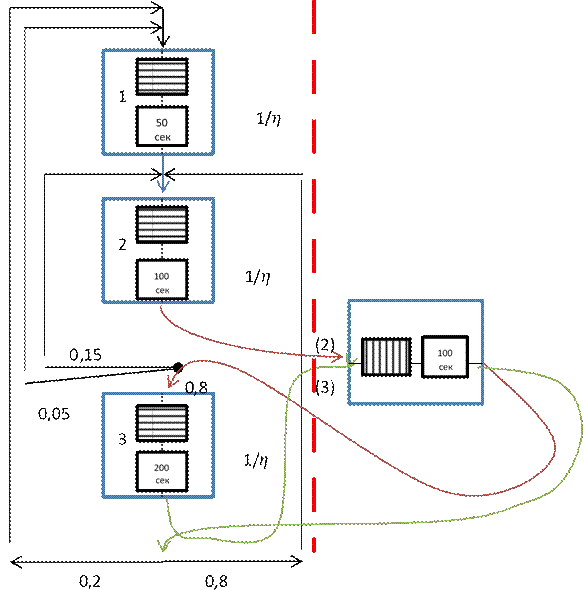
После 2 операции запрос на сервер и 3. 2 и 3 100сек
Исходные данные – число различных тех процессов 3 (ручных)
|
1 |
2 |
3 |
||
|
По техпроцессу |
||||
|
Обращение к машине |
0 |
2 |
3 |
|
|
Время выполнения операции |
50 |
100 |
200 |
|
|
Q(1) матрица вероятностей переходов |
|
|||
|
По системе обработки |
||||
|
Время обработки сообщения |
100 |
100 |
100 |
|
|
матрица вероятностей передач сообщений P (2)=P(3) |
|
Распилили пополам 1 - слева и 0- справа |
||
Найти загрузку оператора ![]() и системные и сетевые характеристики
(для системы слева и системы обработки справа) - Tq(2), Tq(3), время цикла
и системные и сетевые характеристики
(для системы слева и системы обработки справа) - Tq(2), Tq(3), время цикла
Воспользуемся методом декомпозиции и (см 2 курс) сопряжения потоков, для этого представим сеть замкнутой сетью и систему обработки – разомкнутой сетью, рассмотрим их отдельно. В замкнутой циклич сети с 1 заявкой - очередей нет – буфер можно не рисовать. Только приборы.
+Tq(2) +Tq(3)
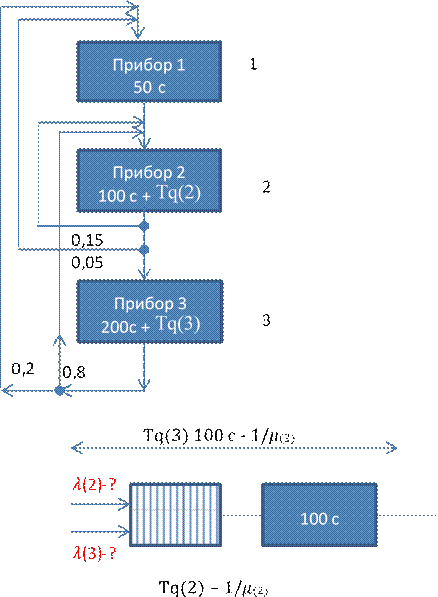
![]() (2) - интенсивность потока заявок, кот
поступают в сист когда 2 операция является первой (начальной)
(2) - интенсивность потока заявок, кот
поступают в сист когда 2 операция является первой (начальной)
![]() (3) - интенсивность потока заявок, кот
поступают в сист когда 3 операция является первой (начальной)
(3) - интенсивность потока заявок, кот
поступают в сист когда 3 операция является первой (начальной)
Для этого используем преобразование рисунка (модели), когда первая операция начальная, вторая - начальная и третья - начальная. Так чтобы был источник и сток заявок. Это можно сделать, поскольку в сети всего 1 заявка. Перерисум рисунок на 3 рисунка (1-начало-2-3,2-3-1, 3-1-2)
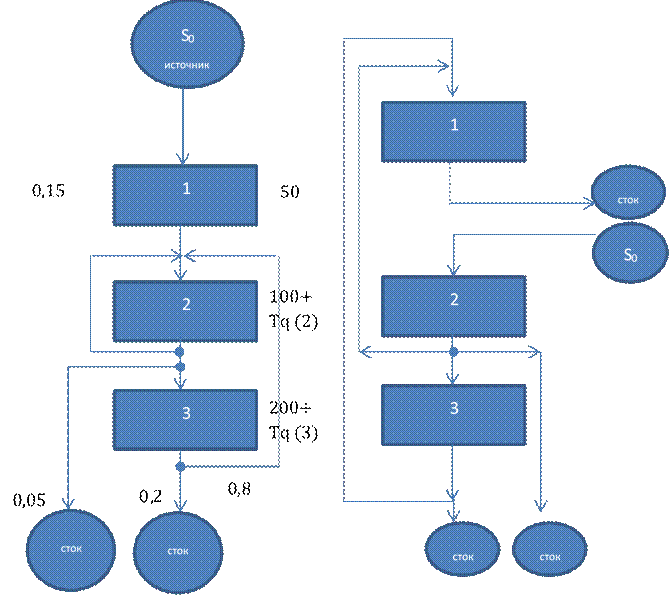
Имеем 3 разомкнутые сети с 1 заявкой, найдем среднее время цикла для разомкнутой сети.
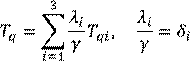
![]() – внешние потоки,
– внешние потоки, ![]() – внутренние
– внутренние
![]()
![]()
![]()
Надо найти коэффициенты передач (определяются матрицей вероятностей передач)
![]()
E-единичная матрица, P- вероятности потока из источника из 1 системы,
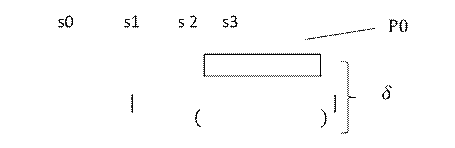
![]() s0
s0
![]() s1 s2 s3
s1 s2 s3
[( ) ( )] ( )
![]()
| |
( )
0010
1000
0,15 … 0,8 …
…
![]()
[(
Решив 1 ур найдем
• ![]() 11=1
11=1
• ![]() 12
=100/21
12
=100/21
• ![]() 13
=80/21
13
=80/21
Для 2 ур
• ![]() 21
=0,21
21
=0,21
• ![]() 22
= 1
22
= 1
• ![]() 32
= 4/5
32
= 4/5
Для 3 ур
• ![]() 13=
21/80
13=
21/80
• ![]() 23=5/4
23=5/4
• ![]() 33=1
33=1
![]()
|
|
|
|
|
|
Все ![]() подставляем в выражение
для Tц, получаем систему
подставляем в выражение
для Tц, получаем систему
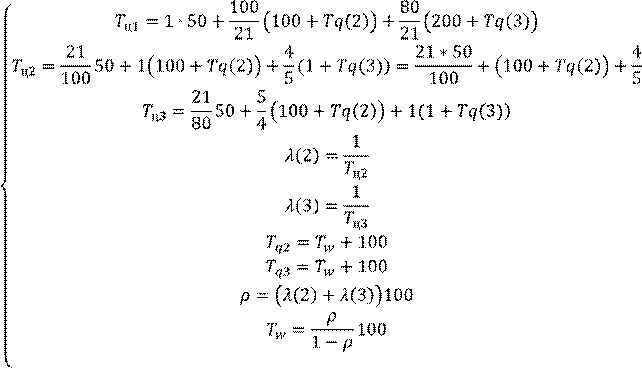
Решив систему, получим загрузку оператора :
… Маткат Tw=50,4![]() системы
обработки =0,33 В числителе убираем машинные операции Tq(2) = 154 и
Tq(3)=154,42
системы
обработки =0,33 В числителе убираем машинные операции Tq(2) = 154 и
Tq(3)=154,42

Не больше 0,75 иначе растет задержка!
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.