H9 = (М9 + H8)2 mod85= (14 + 9)2mod85 = 19
H10 = (М10 + H8)2 mod85= (1 + 19)2mod85 = 60
H11 = (М11 + H10)2 mod85= (13+ 60)2mod85 = 59
H12 = (М12 + H11)2 mod85= (33 + 59)2mod85 = 49
H13 = (М13 + H12)2 mod85= (18 + 49)2mod85 = 69
H14 = (М14 + H13)2 mod85 = (19 + 69)2mod85 = 9
H15 = (М15 + H14)2 mod85= (15 + 9)2mod85 = 66
H16 = (М16 + H15)2 mod85= (33 + 66)2mod85 = 26
H17 = (М17 + H16)2 mod85 = (19 + 26)2mod85 = 70
H18 = (М18 + H17)2 mod85= (28 + 70)2mod85 = 84
H19 = (М19 + H18)2 mod85= (18 + 84)2mod85 = 34
H20 = (М20 + H19)2 mod85= (32 + 34)2mod85 = 21
H21 = (М21 + H20)2 mod85= (24 + 21)2mod85 = 70
Таким образом, хэш-код сообщения H = 70. Для преобразования его в электронную цифровую подпись необходимо выполнить процедуру шифрования с помощью алгоритма RSA.
1) s = (p-1)(q-1) = 4*16 = 64
d = 3 – взаимно простое с s (64 нацело не делится на 3)
2) (e*d)mods = 1
(e*3)mod64 = 1
(e*3) = 64+1 = 65 – нет целочисленного решения (65 не делится нацело на 3)
(e*3) = 64*2+1 = 129, есть решение (129/3 = 43), поэтому e = 43
Открытый ключ: (e; pq) = (43; 85)
Секретный ключ: (d; pq) = (3; 85)
Зашифровав свертку с помощью секретного ключа, получим электронную цифровую подпись:
C = Hemodn
C = 7043mod85 = 80 ()
80 ≠ 21, следовательно отправителю не следует высылать сто тысяч!
Задача №18
ДАНО: Следующая схема техпроцесса:
![]()
ТРЕБУЕТСЯ: Вычислить коэффициенты передач между операциями техпроцесса относительно всех четырех операций.
РЕШЕНИЕ:
Строим матрицу вероятностей перехода:
|
1 |
2 |
3 |
4 |
|
|
1 |
0 |
1 |
0 |
0 |
|
2 |
0 |
0,3 |
0,7 |
0 |
|
3 |
0,6 |
0 |
0 |
0,4 |
|
4 |
1 |
0 |
0 |
0 |
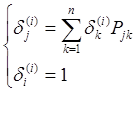
Система 1
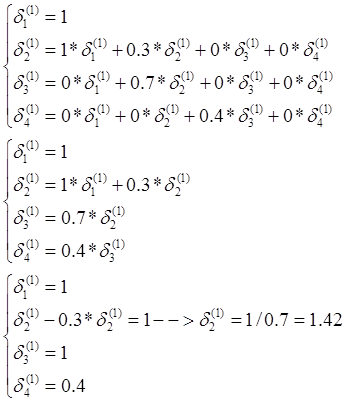
Система 2
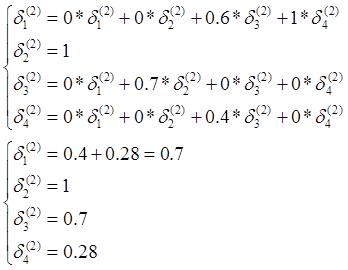
Система 3
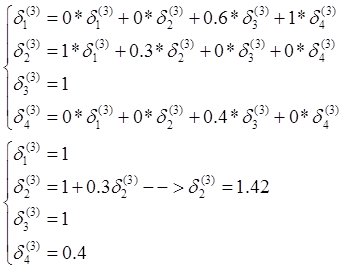
Система 4
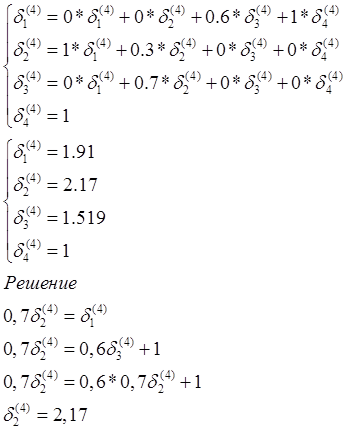
Задача №19
ДАНО: ЭВМ, имеющая показательное распределение наработки до отказа.
ТРЕБУЕТСЯ: Определить, какова должна быть средняя наработка до отказа Т, чтобы вероятность безотказной работы Р(t) была не менее 0,99 в течении наработки t = 300 часов.
РЕШЕНИЕ:
Экспоненциальное (показательное) распределение:
Непрерывная случайная величина x имеет показательное распределение с параметром l>0, если плотность распределения px (x) и функция распределения Fx (x) случайной величины x имеют соответственно вид:
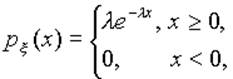
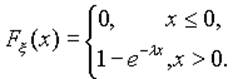
Видно, что показательно распределенная случайная величина принимает только неотрицательные значения.

Задача №20
ДАНО: СОД, имеющая показательное распределение наработки до отказа. Вероятность безотказной работы СОД в течении наработки (0,100) часов равна 0,99.
ТРЕБУЕТСЯ: Вычислить без применения таблиц показательной функции exp(x) среднюю наработку до отказа Т.
РЕШЕНИЕ:

Задача №21
ДАНО: Математическая модель СОД в виде одноканальной СМО типа М/М/1.
ТРЕБУЕТСЯ: Найти: параметры СМО λ, μ, при которых время пребывания в системе для 90% заявок не будет превосходить 20 секунд:
p( w : tq(w ) < 20 cек ) = 0.9
ОГРАНИЧЕНИЯ:
· Загрузка прибора СМО равна 0.9.
· При найденных λ, μ, вычислить все показатели производительности СМО.
РЕШЕНИЕ:
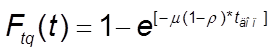 , где
, где
![]() - max время заявки в системе
- max время заявки в системе
С учетом исходных данных:
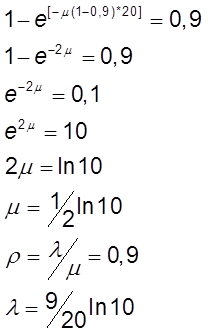
Найдем показатели производ. СМО:
1. Загрузка системы
![]()
2. Загрузка канала
![]()
3. Вероятность простоя обсл. прибора
![]()
4. Коэфф. использования системы
![]()
5. Вер-ть отказа в обслуживании
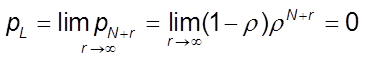
6. Вер-ть обслуживания заявки
![]()
7. Абсолютная пропускная способность системы
![]()
8. Ср. число занятых приборов
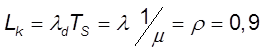
9. Коэфф. использования тракта
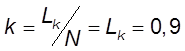
10. Ср. число заявок в очереди
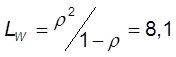
11. Ср. число заявок в системе
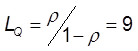
12. Ср.время ожид. начала обслуж.
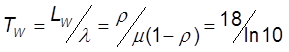
13. Ср.время пребывания в системе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.