Линейное отображение и его матрица. Собственные векторы оператора. Матрица оператора зеркального отражения относительно прямой

Практические упражнения

Линейное отображение и его матрица

Задача  1.

Пусть   - базис линейного пространства  ,  

 - собственные векторы линейного оператора

 с собственными значениями    соответственно.  Найти матрицу  линейного оператора  ,  использовав матрицу оператора  в базисе   составленном из собственных векторов.

Задача  2.

Пусть   - базис линейного пространства  ,  

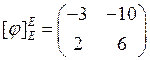, матрица  линейного оператора    в базисе   ,    .

Найти собственные векторы  оператора  .

Задача  3.

Пусть  - пространство многочленов степени не выше чем  2,  - его базис.

Показать, что оператор сдвига  аргумента на число 

,  

является линейным.  Найти  матрицу  .

Задача  4.

Пусть  - пространство многочленов степени не выше чем  2,  - его базис.

Показать, что оператор дифференцирования

,  

является линейным.  Найти  матрицу оператора   в базисе 

используя матрицу .

Задача  5.

Пусть  - пространство многочленов степени не выше чем  2,  - базис .

Показать, что оператор

,  

является линейным.  Найти  базис ядра этого оператора.

Задача  6.

Построить матрицу оператора ортогонального проектирования на прямую

в  каноническом базисе пространства  .

Задача  7.

Построить матрицу оператора зеркального отражения относительно прямой

в  каноническом базисе пространства  .

Задача  8.

Построить матрицу оператора ортогонального проектирования на линейную оболочку (плоскость)   

    

                  

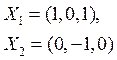
в  каноническом базисе пространства  .

Задача  9.

Построить матрицу оператора зеркального отражения относительно плоскости    

    

                  

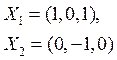
в  каноническом базисе пространства  .

Задача  9.

Пусть   матрица линейного отображения     в  базисе  ,  - координаты вектора   в базисе , - новый базис пространства , причем 

1. Вычислить  , если                                                                                                                       .
2. Вычислить  , если  .

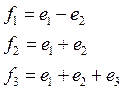
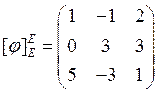Задача  10.

Пусть    - базис в пространстве многочленов степени .                    1.  Построить матрицу   оператора  

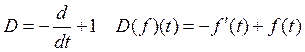
2.  Найти  матрицу   оператора  обратного к  оператору .

3.  Решить уравнение   относительно многочлена   для

•  
•  
• Сделать проверку полученных решений подстановкой решений в соответствующее уравнение.

Метод Гаусса. Системы линейных уравнений

Задача  10.

Дана система векторов   в  пространстве

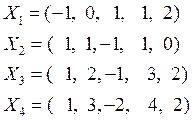
1.  Найти ранг  и базис    линейной оболочки  данной системы векторов.

2.  Найти координаты вектора

в базисе

Задача  11.

Дана система векторов   в  пространстве

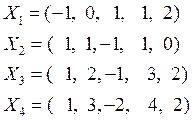
Лежит ли вектор

в линейной оболочке   системы векторов ?

Задача  11.

Найти общее решение системы    уравнений

  

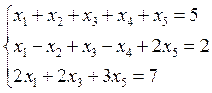
Задача  13.

Линейное отображение  задано так

где

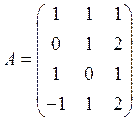
Постройте  базис     ядра  отображения   .

Задача  14.

Линейное отображение  задано так

где

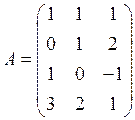
Постройте  базис     ядра  отображения   .

Скалярное произведение

Задача  12.

Пусть  - базис евклидова пространства.

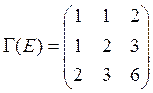
матрица Грама  системы .  Найти угол между  векторами   если

.

Задача  12.

Пусть  - базис евклидова пространства.

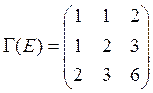
матрица Грама  системы .  

Используя метод  Грама-Шмидта,  построить ортонормированный базис

Задача  13.

Пусть  - базис евклидова пространства.

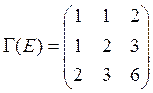
матрица Грама  системы .   Построить базис     дуальный базису   .

Задача  14.

В четырехмерном пространстве  задан тетраэдр  с вершинами

 

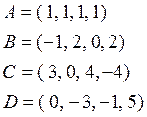
Найти площадь грани   тетраэдра.

Найти расстояние от вершины   до плоскости  треугольника  .

Задача  15.

В четырехмерном пространстве  задан тетраэдр  с вершинами

 

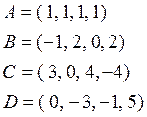
Найти угол между ребром    и плоскостью  треугольника  .

Задача  16.

В четырехмерном пространстве  задан тетраэдр  с вершинами

 

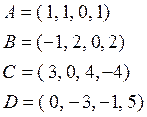
Найти объем тетраэдра и  расстояние от вершины   до плоскости  треугольника  .

Задача  17.

Дана система векторов  

 

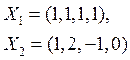
в пространстве  .

Построить  проекцию вектора   на линейную оболочку  .

Задача  18.

Дана система векторов  

 

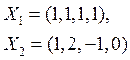
в пространстве  .

Найти  - расстояние от вектора   до  линейной оболочки  .

Задача  19.

Дана система векторов  

 

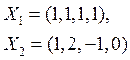
в пространстве  .

Построить базис ортогонального дополнения  линейной оболочки  .

Задача  20.

Дана система векторов  

 

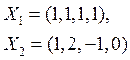
в пространстве  .

Построить ортонормированный базис  линейной оболочки  .

Задача  21.

Дана система  векторов в пространстве  , где   

 

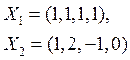
Разложить вектор   в сумму двух ортогональных векторов  , где   -  линейная оболочка  системы векторов  . Проверить, что .

Задача  22.

Задана система линейных уравнений

                  (*)

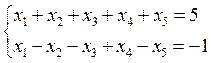Найти ортогональную проекцию точки    на плоскость  , заданную системой уравнений (*).

Задача  23.

Задана система линейных уравнений

                  (*)

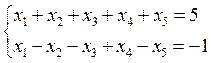Найти расстояние от  точки    до плоскости  , заданной системой (*).

Задача  24.

Система линейных уравнений

                  (*)

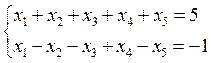задает плоскость . Определить  размерность этой плоскости.

Построить ортогональный базис  нормального пространства  к плоскости .

Задача  25.

Двумерная плоскость    в   задана  параметрически 

,           (1)    где 

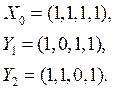
Построить систему уравнений, для  которой  (1)  является её общим решением.

Задача  26.

В пространстве   задана  параметрически плоскость  

,    (1)

где

и плоскость

,  (2)

где

Выписать систему линейных уравнений, определяющую пересечение этих плоскостей (Множество решений этой системы – точки пересечения плоскостей   и ).

Указание.  Построить системы уравнений, определяющие плоскости  и .

Задача  27.

В пространстве   плоскость  задана  параметрически

,    (1)

где

Найти ортогональную проекцию точки   на эту плоскость.

Задача  27.

В пространстве   задана  параметрически плоскость  

,    (1)

где

Найти расстояние от точки   до  этой плоскости.

Задача  28.

В пространстве многочленов скалярное произведение многочленов    задано