Общие вопросы систем электроснабжения. Потребление электроэнергии и электрические нагрузки промышленных предприятий, страница 12

Все необходимые исходные данные приведены в задании на КР 1. К расчетам прилагается чертеж формата 12 по образцу рис. 3. Внимательно изучить МУ к теме 4. Следует иметь ввиду, что проектируемые КТП питаются от КЛ, проходящих через блок цехов 2, где к ним, очевидно, присоединяются другие ТП, следовательно, схема питания магистральная. При этом, цеховые трансформаторы присоединяются к КЛ через выключатель рнагрузки (если S_т > 400 кВА), или через разъединитель (если S_т £ 400 кВА) в комбинации с предохранителями. При этом предохранители устанавливают до выключателя нагрузки и после разъединителя, cчитая по направлению мощности.

ПРИЛОЖЕНИЕ

Применение ЭВМ для определения места

расположения источника питания

При проектировании системы электроснабжения промышленного предприятия решается следующая задача.

Для заданной группы приемников электроэнергии, координаты (x_i, y_i),  i = 1, …, n место расположения и нагрузки которых известны, требуется найти такое месторасположение источника, чтобы затраты на построение и эксплуатацию электрической сети данной группы приемников были бы минимальными.

Для решения этой задачи выберем косвенный критерий

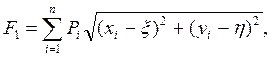                             (П1)

минимизация которого приводит к минимизации функции приведенных затрат. Здесь x и h – координаты искомого месторасположения источника питания.

Теперь можно дать математическую формулировку задачи: требуется найти такие значения x и h, при которых целевая функция (П1) примет наименьшее значение.

Для решения этой задачи используем аналитический метод нахождения экстремума функции двух переменных:

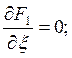
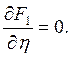                                             (П2)

Решая эти два уравнения относительно x и h, найдем, что оптимальным месторасположением источника питания для заданной группы приемников электроэнергии является точка, координаты которой определяются по формулам:

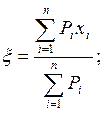
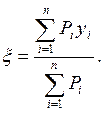                                        (П3)

Математическая формулировка задачи: требуется найти такие значения x и h, при которых целевая функция примет наименьшее значение.

В данной задаче мы имеем функции двух переменных, унимодальную, т.е. имеющую единственный минимум. Для исследования функций такого вида может быть использован метод покоординатного спуска.

Рассмотрим общие положения этого метода.

Пусть задана функция z = f(N) = f(x₁, x₂, …, x_n), минимум которой необходимо найти. Здесь через N сокращенно обозначены точки n-мерного пространства с координатами x₁, x₂, …, x_n. Выбирают произвольную точку М_о = (x_1.0, x_2.0, …, x_n,0) и рассматривают функцию f(N) при фиксированных значениях всех переменных, кроме первой: f(x₁, x_2.0, х_3,0 …, x_n,0). Таким образом, функция f(N) превращается в функцию одной переменной х₁. Изменяя эту переменную, начинают двигаться от начальной точки х_i = х_i,0, в сторону убывания функции, пока не доходят до ее минимума при            х₁ = х_1,1, после которого эта функция начинает возрастать. Точку с координатами (х_1,1, х_2,0, х_3,0, …, х_n,0) обозначим через N₁. Причем f(M₀) ³ f(M₁).

Далее фиксируют все переменные, кроме второй х_i2 и рассматривают функцию f(N) одной переменной х₂: f(x_1,1, x2, x_3,0 …, x_n,0). Изменяя х₂, опять начиняют двигаться от начального значения х₂ = х_2,0 в сторону убывания функции, пока не доходят до минимума при х₂ = х_2,1. Точку с координатами (х_1,1, х_2,1, х_3,0, …, х_n,0) обозначим через М₂. Причем f(M₁) ³ f(M₂).

Проводят такую же минимизацию целевой функции по переменным х₃, х₄, …, х_n. Дойдя до конца, снова возвращаются к переменной х₁ и продолжают процесс. При помощи описанной процедуры получают последовательность точек М₀, М₁, М₂,…, которой соответствует мо-нотонная последовательность значений функции f(M₀) ³ f(M₁) ³ f(M₂) ³ … Обрывая ее на некотором шаге S, можно приближенно принять значение функции f(M₂) за ее наименьшее значение в рассматриваемой области.