Однородности построчных дисперсий. Число степеней свободы для числителя и знаменателя в формуле

Примечание: значения "Р" нагрузок узлов 1 и 2 могут изменяться в диапазоне ±20% от указанных значений, а коэффициенты мощности ( cos j₁ и cos j₂) изменяются в пределах ( 0,7 - 0,9).

Исходные данные по вариантам задания

Таблица 1

Краткие методические указания:

Модель ∆Р=f(P₁, P₂) имеет 2 фактора и по условию задания требуется построить линейную модель, следовательно, она имеет вид: ∆Р=b₀+b₁∙P₁+b₂∙P₂ .

Мощности Р₁ и Р₂ и их диапазоны изменения известны,  известны также диапазоны изменения cos j₁ и cos j₂ . Зная косинусы можно рассчитать реактивные нагрузки узлов по известной формуле 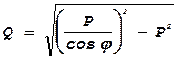, однако заранее неизвестно с каким косинусом работает та или иная нагрузка. В этом случае приходится перебирать все сочетания (наборы) косинусов, чтобы определить реактивные нагрузки по узлам, и это учитывать в потерях.

“Имитационные” опыты (расчеты) выполняют в следующем порядке:

1)   Задаются набором (cos j1, cos j2 ) в различных сочетаниях, т.е.:  (0,7; 0,7), (0,7; 0.9), (0,9; 0,7), (0,9; 0,9). Таким образом, набор  cosj₁=(0,7; 0,7; 0,9; 0,9),а набор cosj₂=(0,7; 0,9; 0,7; 0,9).

2)  В соответствии с планом эксперимента и кодированным значением х_j (табл. 2) определяют значение  в натуральных единицах, т.е. Р_j=Р₀+x_j×dР; для каждого опыта, т.е. Р_j,1 и Р_j,2 (j=1, 2,3,4 - номера опытов). Здесь P₀ – значение в середине диапазона изменения ( табл. 1), а dР=Р_макс-Р₀ ( или  dР=Р₀-Р_мин ) – диапазон изменения нагрузки относительно Р₀ . Максимальные и минимальные значения мощностей находятся как P_макс=Р₀+0.2∙P₀ ;  P_мин=Р₀-0.2∙Р₀ . Эти значения в кодированных значениях “x” соответственно равны (+1) и (-1).

                        Расчеты заносим в информационную таблицу 2.

3)  Находят для каждого опыта реактивные нагрузки узлов в соответствии с принятыми наборами cosj₁ и cosj₂ т.е:

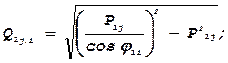
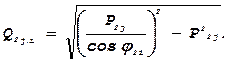  (j=1,2,3,4), (i=1,2,3,4).

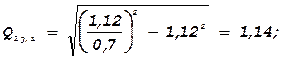
4) Определяют потоки мощностей по ветвям схемы  и вычисляют суммарные потери активной мощности (DР_j,1 , DР_j,2 , DР_j,3 ,  DР_j,4) для всей сети в соответствии с полученными наборами  Q1_j,i и Q2_j,i . Значения (DР_j,1 , DР_j,2 , DР_j,3 ,  DР_j,4 ) можно рассматривать как  результаты “дублирующих” опытов (число их: n=4). Заметим, что расчет DР для разных сочетаний cos j1 ,      cos j2 позволяет неявно учесть в регрессионной модели составляющую потерь от реактивной нагрузки.

5) Для каждого опыта находят средние значения  как :  .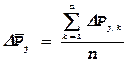

6) Для каждого опыта определяют его дисперсию, т.е.: .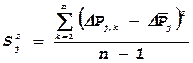

Информационная таблица

Таблица 2

7) Проверяют однородности построчных дисперсий. Это  можно выполнить по критерию Фишера: сначала рассчитывают наблюдаемое значение критерия Фишера, т.е. 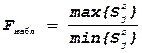,  а затем по таблицам [3] определяют критическое значение критерия, т.е. F_кр=F_{0.05,n1, ,n2}  , где  n1 = n-1 = 3, n2 = n-1 = 3 – число степеней свободы для числителя и знаменателя в формуле для .   .

Так как F_набл<F_кр, то гипотеза об однородности дисперсий принимается.

8) После этого вычисляется дисперсия ошибки всего эксперимента: 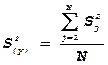  , где N =4 – число опытов (число строк матрицы "x" ).

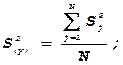
9) Коэффициенты уравнения регрессии   DP = b_o+b₁ ∙x₁+b₂ ∙x₂ вычисляют обычным способом, т.е. или в матричном виде B=(x^T ∙x)^-1 ∙x^T ∙  ,находим матрицы экспериментов х где  – столбец средних значений, или по простым формулам для ортогональной матрицы планирования: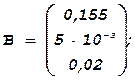   

10) Находят оценки дисперсий коэффициентов b_i (i = 0, 1, 2) уравнения регрессии. Это можно сделать как в матричном виде для общего случая, т. е. вычисляя матрицу дисперсий-ковариаций  D = (x^T×p×x)^-1×S²_(y) , где р – диагональная матрица с числом дублирующих опытов (в ней на месте диагональных элементов стоят значения n (для нашего случая n=4), а остальные элементы равные нулю. 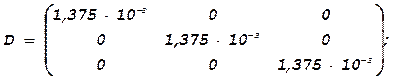       Как видим, оценки дисперсий  коэффициентов для ортогонального плана (а у нас именно такой план) получаются  одинаковыми.

11) Проверяют адекватность линейного уравнения регрессии по критерию Фишера: 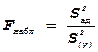,  где  ,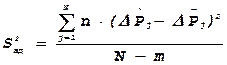

 расчетное ( ) и среднее ( 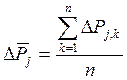) значение функции "∆Р"  для j-го опыта;   m - число коэффициентов модели (с учетом  b_o).   F_кр=F_{0.05,n1, ,n2}   (n1 = N-m=4-3=1 , n2 = N×(n-1) = 4∙(4-1)=12 – число степеней свободы для числителя и знаменателя в формуле для  ).  F_кр также можно найти по таблицам [3]. Если F_набл<F_кр  , то считается, что модель адекватно описывает опытные