Тепло приходит к воде или уходит из воды через слой резины, который в данном случае является приемной площадкой системы (рис. 2.3, а), поэтому максимальная температура воды не может превышать температуру слоя резины. Действительно, в равновесии, когда вода уже нагрета, они равны друг другу. Теплоемкость тонкого слоя резины много меньше теплоемкости воды и термическое кондуктивное сопротивление слоя пренебрежимо мало. Рассмотрим черный резервуар и его содержимое как один сложный объект, имеющий температуру Tp = Tf; коэффициент поглощения a = 0,9; теплоемкость Сf = mc. (Для простоты пренебрегаем тем, что в действительности вода у поверхности емкости будет горячее, а на дне холоднее.) В таком приближении в (2.2) сопротивление Rpf = 0 и hpf = 1.
Из (2.1) и (2.3) с учетом tcou = 1, что соответствует отсутствию покрытия, получаем:
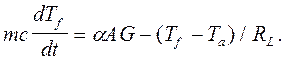(2.5)
На эквивалентной диаграмме (рис. 2.3,б), представляющей собой аналог электрической цепи, G соответствует источнику тока, Сf - емкость между Тf и реперной точкой Тref. Температура Тref произвольна, но фиксирована и не зависит от времени. Это соответствует тому, что производную dTf /dt в левой части уравнения (2.5) можно заменить на производную d(Tf - Тref) / dt, где dТref / dt = 0. Удобно в качестве Тref выбирать Тref = 0° С. Если температура окружающей среды не зависит от времени, можно положить Тref = Та; аналогия с электрическим контуром при этом сохраняется, и остается справедливым уравнение теплового баланса (2.5). "Напряжение" источника тока в правой части эквивалентного контура составляет Та - Тref (не обязательно постоянное).
Сопротивление RL между приемной поверхностью и окружающей средой включает потери тепла как от крышки, так и от дна приемника. Для данной системы и крышка, и дно емкости одинаково взаимодействуют с окружающей средой, так что от их суммарной поверхности площадью А = 2 м2 конвективный и радиационный потоки тепла на эквивалентной диаграмме могут быть изображены параллельными (рис. 2.3, в).
Во многих случаях потери тепла вследствие излучения и конвекции не равны. Конвективный перенос тепла происходит от емкости к окружающей среде с температурой Та, а радиационный - к верхним слоям атмосферы с температурой Тs и/или к окружающей среде. На рис. 2.3, г представлена полная эквивалентная диаграмма для тепловых потерь RL, в которой учтено, что перенос тепла происходит к средам с различными, возможно меняющимися температурами. В данном примере Тs и Та считают постоянными.
Сопротивление конвективным теплопотерям:
,
(2.6)
где коэффициент теплопередачи -
Вт·м2·К-1
. (2.7)
Значения расчетных коэффициентов в выражении (2.7), берутся из справочной литературы [3].
Радиационный поток тепла к верхним слоям атмосферы определен уравнением:
, (2.8)
где эффективная температура неба Тs = Та - 6; s = 5,67*10-8 Вт/(м2*К4) - постоянная Стефана - Больцмана.
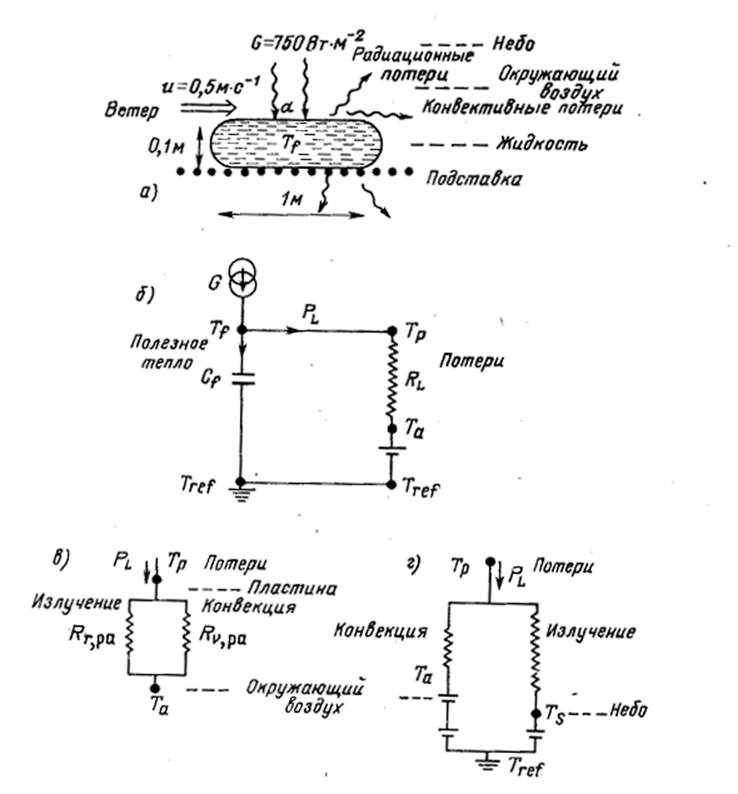
Рис. 2.3. Солнечный нагреватель с черной поверхностью:
а - физическая диаграмма; б - упрощенная эквивалентная диаграмма; в - сопротивление RL представлено в виде параллельных сопротивлений, соответствующих радиационным и конвективным теплопотерям от поверхности нагревателя к окружающей среде с одной температурой Та; г - сопротивление RL показано в виде параллельных компонент, соответствующих конвективным теплопотерям от поверхности нагревателя к окружающей среде с Та, а радиационным - к верхним слоям атмосферы, характеризующимся температурой неба TS, т.е. разным и, возможно, меняющимся температурам.
Выражение (2.8) для потока тепла запишем в виде:
. (2.9)
Тождественное равенство с (2.8) выполняется, если положить:
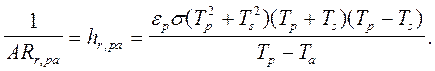(2.10)
Таким образом, можно представить потери тепла в виде, показанном на рис. 2.3, в, где сопротивление RL = (1/Ru, pa + 1/Rr, pa) связывает поверхность приемника излучения с окружающей средой в соответствии с (2.5). Можно показать, что hr, pa слабо зависит от Тp. Полагая Тp = 40° С, находим hr, pa = 7,2 Вт·м-2·К-1, r pa = 0,031 м2·К·Вт-1 и RL = 0,015 К·Вт-1.
Максимально возможная температура достигается, когда имеет место баланс подводимого тепла и потерь, и выражение (2.5) преобразуется в (2.1) с Pnet = 0:
(2.11)
Итак, для рассматриваемого резервуара Тf = 31° С.
Оценим время, необходимое для достижения этой температуры. Скорость, с которой поднимается Тf при средней температуре Тf = 25° С, определим согласно (2.5). Используя рассчитанную величину RL , находим (dTf / dt)25° С = 8,1 · 10-4 К · с-1. Следовательно, время, необходимое для повышения температуры на 11° С, составляет примерно:
ч.
(2.12)
На практике поток солнечного излучения G меняется в течении дня, так что расчеты дают только порядок величин DТ и Dt. Для получения более точных результатов необходимо решать уравнение
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
