interpolation, the interest rate should be approximately 15.1 per cent (0.1 per cent above 15 per cent, or 0.9 per cent less than 16 per cent). Then F = (1 + 0.151)10 = 4.0809, and P = 3,000(F − 1)/(0.151 × 4.0809) = 3,000(4.0809 − 1)/(0.151 × 4.0809) = 14,999, nearly. Thus, the present worth of the net cash flow at 15.1 per cent (−$15,000 + $14,999 = −$1) is only slightly less than 0, and the prospective rate of return may be taken as 15.1 per cent.
|
Year |
Annual Costs Plan A |
Annual Costs Plan B |
Net Cash Flow B — A |
|
0 |
-$15,000 |
-$15,000 |
|
|
1 |
-$8,000 |
-5,000 |
+3,000 |
|
2 |
-8,000 |
-5,000 |
+3,000 |
|
3 |
-8,000 |
-5,000 |
+3,000 |
|
4 |
-8,000 |
-5,000 |
+3,000 |
|
5 |
-8,000 |
-5,000 |
+3,000 |
|
6 |
-8,000 |
-5,000 |
+3,000 |
|
7 |
-8,000 |
-5,000 |
+3,000 |
|
8 |
-8,000 |
-5,000 |
+3,000 |
|
9 |
-8,000 |
-5,000 |
+3,000 |
|
10 |
-8,000
|
-5,000
|
|
|
Totals |
-$80,000 |
-$65,000 |
+$15,000 |
|
a × a = aa = a2 a × a × a = aaa = a3 a × b = ab a2b2 = (ab)2 a2a3 = a2 + 3 = a5 a4 ÷ a3 = a4 – 3 = a a0 = 1 a2 – b2 = (a + b)(a – b) (a + b)2 = a2 + 2ab + b2 (a – b)2 = a2 – 2ab + b2 |
a-----3 = a-b 3 b3 -----a1 = 1- 3 = a–3 3 a (a2)3 = a2 × 3 = (a3)2 = a6 a3 + b3 = (a + b)(a2 – ab + b2) a3 – b3 = (a – b)(a2 + ab + b2) (a + b)3 = a3 + 3a2b + 3ab2 + b3 (a – b)3 = a3 – 3a2b + 3ab2 – b3 |
![]() 3 ab =
3 a × 3
b
3 ab =
3 a × 3
b
![]()
![]()
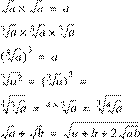 = a a 3
a 3 - = ------b 3 b
= a a 3
a 3 - = ------b 3 b
= a2/3 3 1- = ----1--- = a–1/3 a 3 a
|
When |
|
then then then then Equations |
loga + logb = logx loga – logb = logx 3loga = logx loga --------- = logx 3 |
An equation is a statement of equality between two expressions, as 5x = 105. The unknown quantity in an equation is generally designated by the letter x. If there is more than one unknown quantity, the others are designated by letters also selected at the end of the alphabet, as y, z, u, t, etc.
An equation of the first degree is one which contains the unknown quantity only in the first power, as 3x = 9. A quadratic equation is one which contains the unknown quantity in the second, but no higher, power, as x2 + 3x = 10.
Solving Equations of the First Degree with One Unknown.—Transpose all the terms containing the unknown x to one side of the equals sign, and all the other terms to the other side. Combine and simplify the expressions as far as possible, and divide both sides by the coefficient of the unknown x. (See the rules given for transposition of formulas.)
Example: 22x – 11 = 15x + 10
22x – 15x = 10 + 11
7x = 21
x = 3
Solution of Equations of the First Degree with Two Unknowns.—The form of the simplified equations is
ax + by = c a1x + b1y = c1
Then, cb1 – c1b ac1 – a1c
x = ---------------------- y = ---------------------ab1 – a1b ab1 – a1b
Example: 3x + 4y = 17
5x – 2y = 11
17 × (–2) – 11 × 4 – 34 – 44 –78
x = -------------------------------------------- = ---------------------- = ------- = 3
3 × (–2) – 5 × 4 – 6 – 20 –26
The value of y can now be most easily found by inserting the value of x in one of the equations:
5 × 3 – 2y = 11 2y = 15 – 11 = 4 y = 2
Solution of Quadratic Equations with One Unknown.—If the form of the equation is ax2 + bx + c = 0, then
![]() –
b ± b2
– 4ac
–
b ± b2
– 4ac
x = -------------------------------------
2a
Example:Given the equation, 1x2 + 6x + 5 = 0, then a = 1, b = 6, and c = 5.
![]() – 6 ± 62 – 4 × 1 × 5 (–6) + 4 (–6) – 4
– 6 ± 62 – 4 × 1 × 5 (–6) + 4 (–6) – 4
x = ------------------------------------------------- = -------------------- = –1 or ------------------ = –5
2 × 1 2 2
If the form of the equation is ax2 + bx = c, then
![]() –
b ± b2
+ 4ac
–
b ± b2
+ 4ac
x = ---------------------------------------
2a
Example:A right-angle triangle has a hypotenuse 5 inches long and one side which is one inch longer than the other; find the lengths of the two sides.
Let x = one side and x + 1 = other side; then x2 + (x + 1)2 = 52 or x2 + x2 + 2x + 1 = 25; or 2x2 + 2x = 24; or x2 + x = 12. Now referring to the basic formula, ax2 + bx = c, we find that a = 1, b = 1, and c = 12; hence,
![]() – 1 ± 1 + 4 × 1 × 12 (–1) + 7 (–1) – 7
– 1 ± 1 + 4 × 1 × 12 (–1) + 7 (–1) – 7
x = -------------------------------------------------- = -------------------- = 3 or x = ------------------ = –4
2 × 1 2 2
Since the positive value (3) would apply in this case, the lengths of the two sides are x = 3 inches and x + 1 = 4 inches.
Cubic Equations.—If the given equation has the form: x3 + ax + b = 0 then
b a3 b2 1/3 b a3 b2 1/3
![]()
![]() x
= – 2- + ----27
+ -----4 + – -2 – 27---- + -----4
x
= – 2- + ----27
+ -----4 + – -2 – 27---- + -----4
The equation x3 + px2 + qx + r = 0, may be reduced to the form x13 + ax1 + b = 0 by substi-
p
tuting x1 – -3 for x in the given equation.
Series.—Some hand calculations, as well as computer programs of certain types of mathematical problems, may be facilitated by the use of an appropriate series. For example, in some gear problems, the angle corresponding to a given or calculated involute function is found by using a series together with an iterative procedure such as the Newton-Raphson
method described on page 35. The following are those series most commonly used for such purposes. In the series for trigonometric functions, the angles x are in radians (1 radian = 180/π degrees). The expression exp(−x2) means that the base e of the natural logarithm system is raised to the −x2 power; e = 2.7182818.
|
(1) sin x = x − x3/3! + x5/5! − x7/7! + ··· |
for all values of x. |
|
(2) cos x = 1 − x2/2! + x4 /4! − x6/6! + ··· |
for all values of x. |
|
(3) tan x = x + x3/3 + 2x5/15 + 17x7/315 + 62x9/2835 + ··· |
for |x| < π/2. |
|
(4) arcsin x = x + x3/6 + 1 · 3 · x5/(2 · 4 · 5) + 1 · 3 · 5 · x7/(2 · 4 · 6 · 7) + ··· (5) arccos x = π/2 − arcsin x |
for |x| ≤ 1. |
|
(6) arctan x = x − x3/3 + x5/5 − x7/7 + ··· |
for |x| ≤ 1. |
|
(7) ex =1 + x + x2/2! + x3/3! + ··· |
for all values of x. |
|
(8) exp(− x2) = 1 − x2 + x4/2! − x6/3! + ··· |
for all values of x. |
|
(9) ax = 1 + x loge a + (x loge a)2/2! + (x loge a)3/3! + ··· |
for all values of x. |
|
(10) 1/(1 + x) = 1 − x + x2 − x3 + x4 −··· |
for |x| < 1. |
|
(11) 1/(1 − x) = 1 + x + x2 + x3 + x4 + ··· |
for |x| < 1. |
|
(12) 1/(1 + x)2 = 1 − 2x + 3x2 − 4x3 + 5x4 − ··· |
for |x| < 1. |
|
(13) 1/(1 − x)2 = 1 + 2x + 3x2 + 4x3 + 5x5 + ··· |
for |x| < 1. |
(14) (1 + x) = 1 + x/2 − x2/(2 · 4) + 1 · 3 · x3/(2 · 4 · 6) for |x| < 1.
 − 1 · 3 · 5 · x4/(2
· 4 · 6 · 8) −···
− 1 · 3 · 5 · x4/(2
· 4 · 6 · 8) −···
|
+ ··· |
for |x| < 1. |
|
(16) (a + x)n = an + nan−1 x + n(n − 1)an−2 x2/2! |
for x2 < a2. |
(15) 1 ⁄ ( 1 + x) = 1 − x/2 + 1 · 3 · x2/(2 · 4) − 1 · 3 · 5 · x3/(2 · 4 · 6)
+ n(n − 1)(n − 2)an−3 x3/3! + ···
Derivatives of Functions.—The following are formulas for obtaining the derivatives of basic mathematical functions. In these formulas, the letter a denotes a constant; the letter x denotes a variable; and the letters u and v denote functions of the variable x. The expression d/dx means the derivative with respect to x, and as such applies to whatever expression in parentheses follows it. Thus, d/dx (ax) means the derivative with respect to x of the product (ax) of the constant a and the variable x, as given by formula (3).
To simplify the form of the formulas, the symbol D is used to represent d/dx. Thus, D is equivalent to d/dx and other forms as follows:
D(ax) = d--------------(ax) = ----d (ax) dx dx
1) D(a) = 0 2) D(x) = 1 3) D(ax) = a · D(x) = a · 1 = a
4) D(u + v) = D(u) + D(v) Example: D(x4 + 2x2) = 4x3 + 4x
5) D(uv) = v · D(u) + u · D(v) Example: D(x2 · ax3) = ax3 · 2x + x2 · 3ax2 = 5ax4
6) D(u v⁄ ) = v---------------------------------------------⋅ D(u) – u ⋅ D(v) Example: D(ax2/sinx) = (2ax · sinx − ax2 · cosx)/sin2x
v2
7) D(xn) = n · xn−1 Example: D(5x7) = 35x6
8) D(ex) = ex
9) D(ax) = ax · loge a Example: D(11x) − 11x · loge11
10) D(uv) = v · uv−1 · D(u) + uv · loge u · D(v)
11) D(loge x) = 1/x
12) D(loga x) = 1/x · loge a = loga e/x
13) D(sin x) = cos x Example: D(a · sin x) = a · cos x
14) D(cos x) = sin x 15) D(tan x) = sec2 x
Solving Numerical Equations Having One Unknown.—The Newton-Raphson method is a procedure for solving various kinds of numerical algebraic and transcendental equations in one unknown. The steps in the procedure are simple and can be used with either a handheld calculator or as a subroutine in a computer program.
Examples of types of equations that can be solved to any desired
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.