Информатика и выч. техника \ Информатика

Программа решения системы линейных уравнений методом итераций. Разработка Pascal-программы. Математическая формулировка задачи

Страницы работы

21 страница (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Министерство образования Республики Беларусь

БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра “Горные машины”

КУРСОВОЙ ПРОЕКТ

по дисциплине “ Информатика”

Программа решения системы линейных уравнений методом итераций

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Руководитель:

Исполнитель: студент группы

2002

Содержание

Введение ……………………………………….

1. Постановка задачи

2. Разработка Pascal-программы

2.1. Математическая формулировка задачи

2.2. Список идентификаторов

2.3. Блок-схема алгоритма

2.4. Распечатка текста программы

3. Результаты выполнения программы …………

3.1. Распечатка типовых окон……………………

3.2. Распечатка результатов …………………

3.2.1. Анализ результатов ………………………

Заключение …………………………………………

Список использованных источников ……………

Введение

Первая версия языка программирования Паскаль была

Разработана на кафедре информатики Стэнфордского униврситета швейцарским учёным Никлаусом Виртом в 1968

году .

В 1985 году на рынке ПЭВМ появился язык прогаммирования Турбо-Паскаль (версия 3.0 ) с тех пор Паскаль стал применяться в общеобразовательных проффесионально-технических школах и в сфере высшего образования в качестве первого языка программирования.

С выходом всвет версии 5.0 ТП получил ещё большие шансы на благосклонную реакцию со стороны проффесиональных пользователей благодаря встроенному в среду программирования интегрированному отладчику , который позволил повысить производительность труда.

Набор операторов стандартного Паскаля относительно мал и легко изучаем . Широкое распростронение Паскаля привело к появлению на рынке большого числа прикладных программ.

Подобные программы разработаны для многих проблемных областей , однако задача их настройки в соответствии с требованиями пользователей продолжает оставаться достаточно важной.

Сегодня Паскаль является одним из самых распространённых в мире алгоритмических языков. Ведущие разработчики программных средств: Microsoft и Borland регулярно поставляют на рынок новые версии этого языка.

1. Постановка задачи

Целью данной работы является создание программы, обеспечивающее решение. решения системы линейныхуравнений методом итераций.

Программа должна обеспечивать быстрый доступ пользователя к опытным данным, обеспечивать автоматизацию вычисления корней уравнения и удобный интерфейс с пользователем.

Ввод данных и вывод результатов осуществляется в окне ввода в соответствующем виде

Работа с программой осуществляется посредствам меню, которое содержит три пункта: ”Справка”, ” Расчёт”, , “Выход”.

Управление в программе осуществляется с помощью клавиш управления курсора и клавиатурой.

2. Разработка Pascal-программы:

Математическая формулировка задачи.

РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ

УРАВНЕНИЙ ИТЕРАЦИОННЫМИ МЕТОДАМИ

2.1. Краткие теоретические сведения

Для решения итерационным методом система Ax=b должна быть приведена к виду x = Gx+f , где G - матрица, f - вектор свободных членов. Затем выбирается произвольный вектор x⁽⁰⁾ и строится рекуррентная последовательность векторов x⁽¹⁾, x⁽²⁾,..., x⁽^k⁾,... по формулеx⁽^k⁾ = Gx⁽^k^-1)+f . Для сходимости этой последовательности при любом начальном приближении x⁽⁰⁾ необходимо и достаточно, чтобы все собственные значения матрицы G были по абсолютной величине меньше единицы. На практике пользуются достаточными условиями:

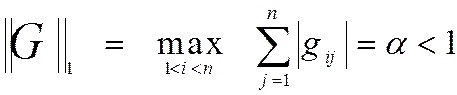или

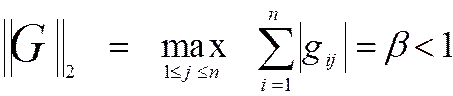
Если матрица A имеет диагональное преобладание, т.е. 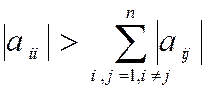, то преобразование системы можно осуществить, просто решая каждое i-ое уравнение относительно x_i. Получившийся итерационный процесс

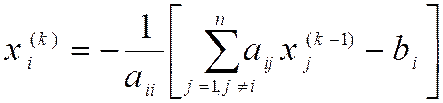
называется методом Якоби (или методом простой итерации).

Модификация метода Якоби, в которой при k-ой итерации для вычисления следующего x_i⁽^k⁾ используются уже вычисленные на этом шаге x₁⁽^k⁾, x₂⁽^k⁾,...,x_i_-1⁽^k⁾, приводит, как правило к ускорению сходимости и называется методом Зейделя .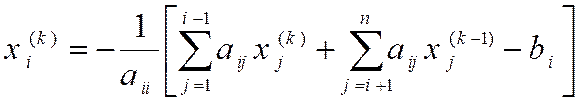

Этот метод может быть реализован на ЭВМ без привлечения дополнительной памяти, т.к.полученное новое значение x_i⁽^k⁾ сразу запоминается на месте старого.

Приведенные выше методы Якоби и Зейделя относятся к одношаговым итерационным методам, когда для нахождения x⁽^k⁺¹⁾ требуется помнить только одну предыдущую итерацию x⁽^k⁾. Иногда используются и многошаговые итерационные методы, в которых x⁽^k⁺¹⁾ определяется через значения x на двух и более предыдущих итерациях.

Очень часто для ускорения сходимости в итерационные методы вводят числовые параметры t_k, которые зависят, вообще говоря, от номера итераци. Способ выбора итерационных параметров определяется при исследовании сходимости метода, когда выясняется при каких значениях параметров метод сходится и при каких значениях параметров сходимость будет наиболее быстрой (соответствующие параметры называются оптимальными). Для исследования сходимости удобнее записывать итерационные методы не в координатной, а в матричной форме, придерживаясь стандартной формы записи итерационных методов

Канонической формой одношагового итерационного метода решения СЛАУ называется его запись в виде

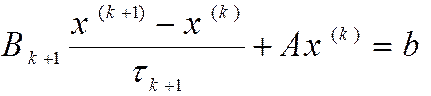
где B_k+1 - матрица, задающая тот или иной итерационный метод, t_k+1 - итерационный параметр. Предполагается, что существуют обратные матрицы [B_k₊₁]^-1. Итерационный метод называют явным, если стационарным, ес B_k+1 - единичная матрица. Неявные итерационные методы имеет смысл применять лишь в том случае, когда каждую матрицу B_k обратить легче, чем исходную матрицу A (т. е. когда решение системы уравнений с матрицей B_k требует меньше машинной памяти или времени или алгоритмически проще, чем решение исходной системы).

Итерационный метод называется ecли B_k+1=B и t_k+1=t, (т.е. не зависят от номера итерации), и нестационарным - в противоположном случае. Согласно этой классификации метод простой итерации является одношаговым явным стационарным методом с диагональной матрицей B (b_ii.= a_ii) и может быть записан в виде , где r⁽^k⁾- вектор невязки.