Статический и тяговый расчет горной гусеничной машины. Теоретические основы и методики статического и тягового расчетов мобильной горной машины на гусеничном ходу

Начало системы осей, в которой определяются координаты центра масс и центра давления, удобнее всего связать с машиной и расположить в центре ее опорной поверхности. В этом случае качество компоновки машины, т.е. рациональность пространственного расположения ее составных частей, оценивается мерой близости центра давления к началу системы координат.

Из механики известно, что координаты центра масс механической системы вычисляются по формулам:

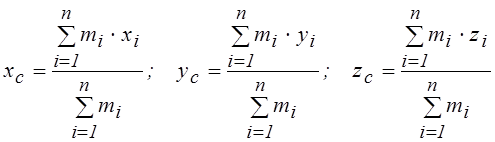,                 (1.1)

где           - масса составной части машины;

 - координаты ее центра масс.

При выполнении задания координаты   задаются, а при проектировании машины они определяются по ее эскизному чертежу. Для удобства вычислений по формулам (1.1) рекомендуется составить таблицу 1.1.

Таблица 1.1

Данные для вычисления координат центра масс

№ п/п	Наименование составной части машины	Обозначение	Масса, кг	Координаты центра масс, м
1	Гусеничный ход		2500	0	0,2	0,5
...	...	...	...	...	...	...

Центром давления машины на грунт называется точка, радиус-вектор которой определяется выражением

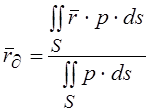,                                             (1.2)

где   - давление машины на грунт в точке с радиус-вектором ;

 - площадь опорной поверхности машины;

 - элемент этой площади.

Иначе, центр давления представляет собой точку приложения равнодействующей сил давления машины на несущее основание. Из последнего определения следует, что эта точка лежит в опорной плоскости гусеничного хода.

Записав (1.2) в проекциях на оси системы координат, получим:

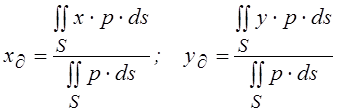.                           (1.3)

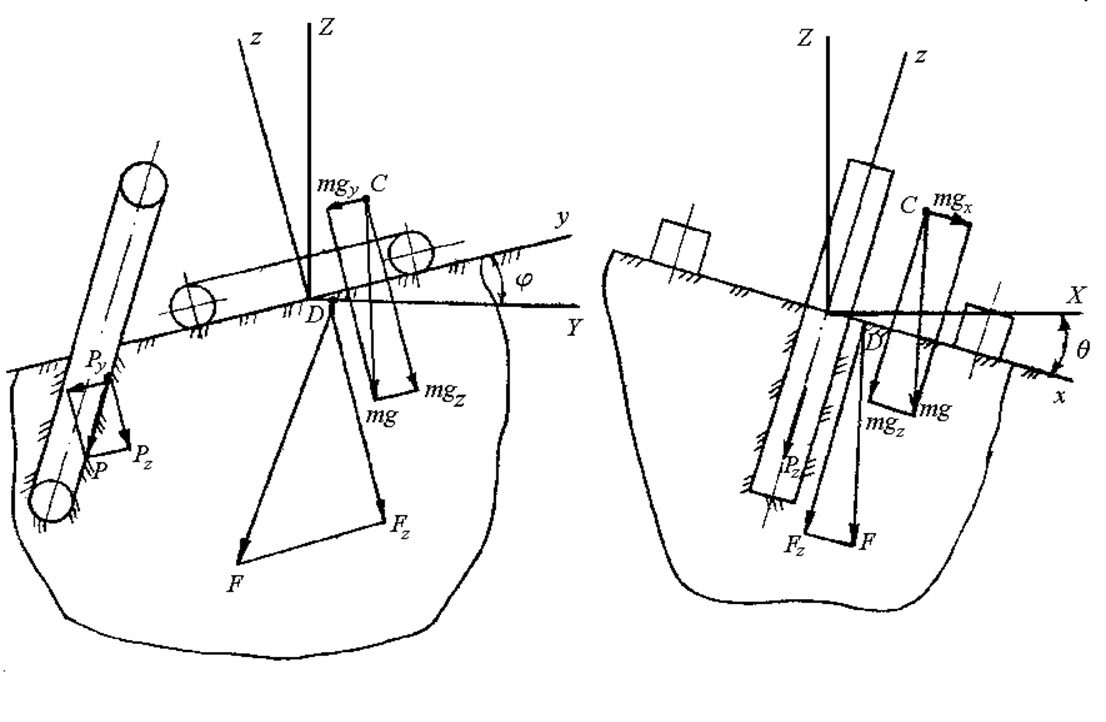
Интегралы в числителе выражений (1.3) представляют собой (рис. 1.1) суммарные моменты сил давления машины на грунт относительно осей    и  , т.е.

.

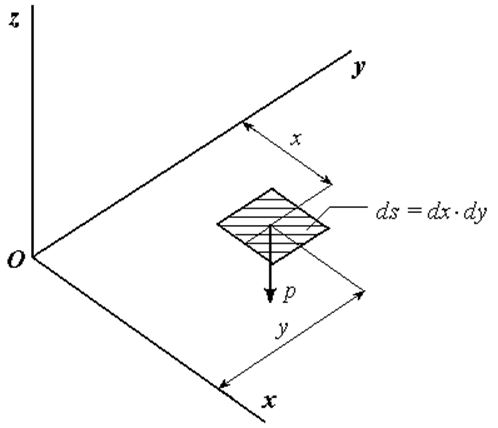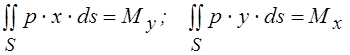Рис. 1.1. К определению моментов   и 

На основании теоремы Вариньона о равенстве момента равнодействующей сумме моментов составляющих можно записать

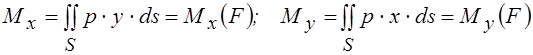, где     - равнодействующая внешних сил, действующих на машину

(исключая силы реакций грунта на ходовое устройство).

Для горных машин равнодействующая   внешних сил представляет геометрическую сумму силы тяжести, приложенной в центре масс, сил реакций разрабатываемой породы на рабочие органы, крюкового усилия и т.п.

Тогда на основании той же теоремы Вариньона (в нашем случае рис. 1.2)

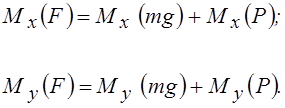                               (1.4)

где   - сила тяжести;

           - равнодействующая внешних сил.

Интеграл, стоящий в знаменателе выражений (1.3), есть общая сила давления машины на несущее основание

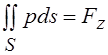, где   - проекция равнодействующей   на ось  , которая направлена нормально к опорной поверхности,

,                                          (1.5)

где     и   - соответственно проекции силы тяжести и равнодействующей внешних сил на ту же ось.

С учетом этого, окончательно

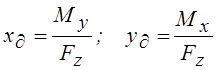,                                   (1.6)

где   и  определяются выражениями (1.4), а  - выражением (1.5).

Направление действия силы  зависит от способа соединения рабочего органа с машиной. Если рабочий орган закреплен на машине жестко, то направление силы  меняется вместе с изменением положения машины, вызываемым неровностью рельефа поверхности или различной деформацией грунта под гусеницами. В этом случае направление силы  зафиксировано в системе осей , связанной с машиной. В ряде машин, предназначенных для рытья осушителей или профилирования поверхности, с целью создания постоянного наклона дна осушителей и требуемого профиля поверхности рабочие органы независимо от положения самой машины сохраняют заданное положение относительно неподвижной (инерциальной) системы осей .

Таким образом, направление силы  у этих машин всегда ориентировано относительно осей . Напомним, что направление силы  совпадает с осью .

Для вычисления ,  и  по формулам (1.4), (1.5) достаточно разложить силы  и  на проекции по осям ,  и . Чтобы это сделать, необходимо знать углы между направлением действия сил и названными осями. В нашем случае часть сил (сила ) легко проектируется на оси системы , а другая часть (сила ) может быть ориентирована как в системе , так и в системе .

Чтобы найти проекции сил в одной системе координат по известным проекциям в другой необходимо знать углы или таблицу направляющих косинусов между осями систем.

Направляющие косинусы определяют посредством углов Эйлера , ,  (рис. 1.3), которые задают ориентацию подвижного триэдра  относительно неподвижного . Перевод триэдра  в положение  осуществляется тремя последовательными поворотами: на угол  вокруг оси , на угол  вокруг оси , с которой совпадает ось  после первого поворота, и на угол  вокруг оси , с которой совпадает ось  после двух предыдущих поворотов. Заметим, что после первого поворота ось  займет положение , ось  после второго поворота совпадает с  и после третьего с , ось  переходит в промежуточное положение  после первого поворота и в положение  после третьего. Углы , ,  называются соответственно углами рысканья, поперечного и продольного крена.

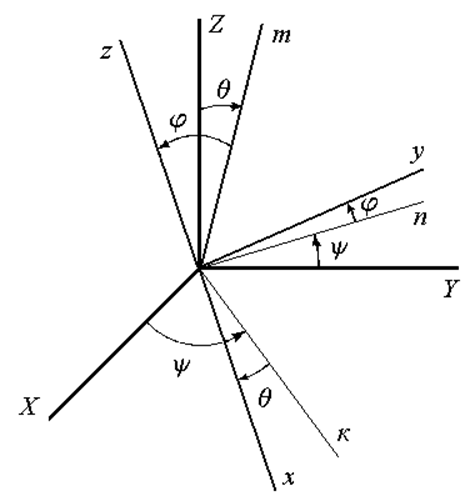Рис. 1. 3. Ориентация подвижных осей

Таблицу косинусов между подвижными и неподвижными осями вычислим как произведение трех матриц направляющих косинусов, образующихся после каждого из перечисленных поворотов. Обозначив эти матрицы, соответственно через ,  и , имеем

.

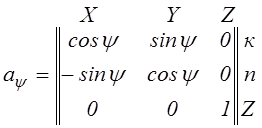Элементы этой матрицы (рис. 1.3) равны косинусам углов между соответствующими осями (например, ).

Аналогично

;

.

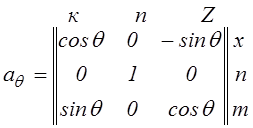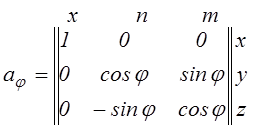Тогда матрица направляющих косинусов определится как произведение трех приведенных матриц [1]

.

Произведя умножение, найдем

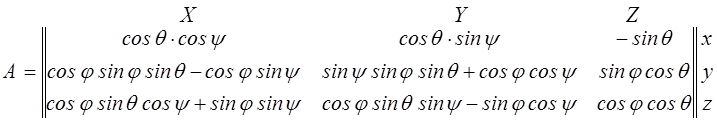(1.7)

При статическом расчете машина рассматривается в состоянии покоя, поэтому , , . Приняв для упрощения , приходим к следующему виду таблицы направляющих