Детеминированные обучающие системы классификации. Изучение детерминированного подхода для создания систем классификации альтернатив

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Тульский государственный университет

Кафедра прикладной математики и информатики

теория выбора и принятия решений

Лабораторная работа № 5

детеминированные обучающие системы классификации

Выполнил: ст. гр.                                                              

Проверил:                                                                                        

Тула 2005

ЦЕЛЬ

Изучить детерминированный подход для создания систем классификации альтернатив.

Описание метода распознавания

Использование методов обучения необходимо, когда отсутствует первоначальная информация об объекте.

Пусть есть априорная информация об объектах, представляющая собой список этих объектов с указанием классов, к которым они относятся. Обозначим объекты списка как , а классы как  . Тогда исходную информацию можно

представить в виде:

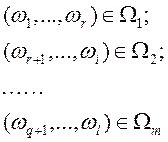
          Каждый объект может быть описан на языке признаков . Исходный список может быть представлен в виде обучающей последовательности

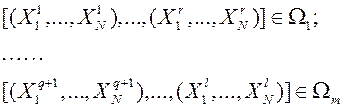
          Если ограничиться рассмотрением двух классов  и , то разделяющая классы гиперповерхность носит название дихотомии. К дихотомии можно свести случай, когда число классов больше двух.

Разделяющая функция , где  представляется скалярным произведением вектора признаков  и неизвестного вектора параметров .

Знание разделяющей функции определяет области в – мерном пространстве признаков. В частности, пространства, соответствующие классам   и  имеют вид

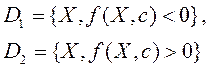
Принцип подкрепления— наказания

Алгоритм перцептрона — простейшая итерационная схема определения весов. Пусть — начальный вектор параметров, который выбирается обычно произвольно. Тогда – й шаг обучения выглядит следующим образом. Если  и , то вектор  заменяется на  , где  — константа, постоянное корректирующее приращение.

Если  и , то вектор  заменяется на  . В случае равенства вектор не изменяется, то есть . Константа  должна быть положительной и в данном алгоритме предполагается постоянной.

Рассмотрим алгоритм разделения объектов на несколько классов, когда допускается существование  решающих функций, обладающих тем свойством, что при   для всех .

Рассмотрим  классов . Пусть на – том шаге итерации процедуры обучения системе предъявляется образ , принадлежащий классу . Вычисляются значений решающих функций

.

Затем если выполняются условия

, то векторы весов не изменяются, то есть .

Если же для некоторого  справедливо , то производятся следующие коррекции весов

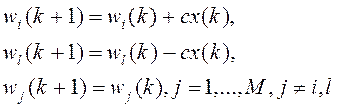
Если классы разделимы, то можно показать, что этот алгоритм сходится за конечное число итераций при произвольных начальных векторах весов.

Выполнение

1. Значения признаков обучающих образов:

, , ,.

2. Начальный вектор весов:

.

Текст программы 

#include <math.h>

#include <iostream.h>

#include <conio.h>

void print(int r,float *m)

{

int i;

cout<<"\n";

for(i=0;i<r;i++)

cout<<m[i]<<" ";

}

float mul(int r,float *x,float *y)

{

float m;

int i;

m=0;

for(i=0;i<r;i++)

m=m+x[i]*y[i];

return m;

}

float* add(int r,float *x,float *y)

{

float *m;

int i;

m=new float[r];

for(i=0;i<r;i++)

m[i]=x[i]+y[i];

return m;

}

float* scal(int r,int a,float *x)

{

float *m;

int i;

m=new float[r];

for(i=0;i<r;i++)

m[i]=a*x[i];

return m;

}

float* dd(int r,int K,float** x,float* y)

{

float *m;

int i;

m=new float[r];

for(i=0;i<K;i++)

m[i]=mul(r,x[i],y);

cout<<"\nvector d:";

print(r,m);

return m;

}

void main(void)

{

int p,l,ind,IND,r,i,j,k,K,*kol_ob;

float c,***x,*d,**w,*rasp;

cout<<"kolichestvo klassov:\n";

cin>>K;

kol_ob=new int[K];

cout<<"korrektiruyuschee priraschenie:\n";

cin>>c;

IND=0;

for(i=0;i<K;i++)

{

cout<<"chislo ob'ektov "<<(i+1)<<" klassa:\n";

cin>>kol_ob[i];

IND=IND+kol_ob[i];

}

cout<<"razmernost' ob'ektov:\n";

cin>>r;

x=new float**[K];

d=new float[K];

w=new float*[K];

for(i=0;i<K;i++)

{

w[i]=new float[r+1];

for(j=0;j<r+1;j++)

w[i][j]=0;

}

for(i=0;i<K;i++)

{

x[i]=new float*[kol_ob[i]];

for(j=0;j<kol_ob[i];j++)

{

x[i][j]=new float[r+1];

}

}

for(i=0;i<K;i++)

{

cout<<"ob'ekty klassa "<<(i+1)<<":\n";

for(j=0;j<kol_ob[i];j++)

{

cout<<"ob'ekt "<<(j+1)<<":\n";

for(k=0;k<r;k++)

{

cin>>x[i][j][k];

}

x[i][j][r]=1;

}

}

getch();

do

{

ind=0;

for(i=0;i<K;i++)

{

for(j=0;j<kol_ob[i];j++)

{

d=dd(r+1,K,w,x[i][j]);