|
Номер столбца |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Комплексы причин |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
|
Комплексы следствий |
|
|
|
|
|||||||
|
Случаи |
|||||||||||
|
1–е полугодие |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
2 |
1 |
2 |
3 |
|
2–е полугодие |
3 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
2 |
Всего 12 случаев.
Диагностическая вероятностная таблица
|
Комплексы
причин |
||||||
|
0 |
1 |
2 |
3 |
|
||
|
Комплексы
следствий |
0 |
|
0 |
0 |
0 |
|
|
1 |
0 |
|
0 |
|
|
|
|
2 |
|
0 |
0 |
0 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассчитаем
условные вероятности появления комплекса следствий![]() при
заданном комплексе причин
при
заданном комплексе причин ![]() по формуле
по формуле
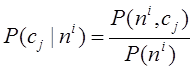 .
.
Тогда искомая таблица условных вероятностей имеет вид:
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
0 |
|
0 |
|
|
|
|
0 |
0 |
0 |
|
|
|
|
1 |
|
Отсюда можно
сделать, например, следующий вывод. Пусть в отделении банка одновременно
уменьшили величину минимального вклада и повысили периодичность начисления
процентов. Тогда вероятность увеличения количества обращений без увеличения
суммы привлеченных средств равна ![]() .
.
Рассчитаем
условные вероятности появления комплекса причин ![]() при
заданном комплексе следствий
при
заданном комплексе следствий![]() по формуле
по формуле
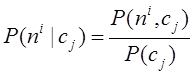 .
.
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
|
|
0 |
|
0 |
|
|
|
1 |
0 |
0 |
0 |
|
|
|
|
|
|
Рассчитаем
скорректированные значения вероятностей. Имеем новое распределение следствий:
комплекс следствий ![]() встречается в 6 случаях;
встречается в 6 случаях; ![]() встречается в 1 случае;
встречается в 1 случае; ![]() встречается в 5 случаях.
встречается в 5 случаях.
Зная предыдущую информацию, по формуле Байеса
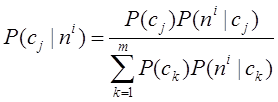
рассчитаем новое распределение вероятностей.
Здесь ![]() — число комплексов
следствий, то есть в нашем случае
— число комплексов
следствий, то есть в нашем случае ![]() ;
; ![]() — известное распределение условных
вероятностей;
— известное распределение условных
вероятностей; ![]() — новая информация. Имеем
— новая информация. Имеем 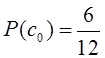 ;
; 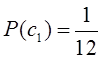 ;
;
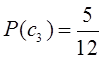 .
.
Тогда получим новое распределение условных вероятностей:
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
0 |
|
0 |
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
1 |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.