

ЛАБОРАТОРНАЯ РАБОТА N 8
1.Цель и задачи.
Разработка моделирующего алгоритма и программы для изучения длины критического пути на сетевом графике как случайной величины.
2.Теоретические сведения.
Если продолжительности работ сетевого графика являются случайными величинами, то и длина критического пу33ти будет случайной величиной. Закон распределения этой случайной величины неизвестен и мы пытаемся получить информацию о нем статистическими методами. Для этого многократно «наблюдаем» нашу случайную величину и обрабатываем полученные данные.
В применении к заданию одно «наблюдение» происходит так:
1. Назначаем продолжительности работам в соответствии с их законами распределения. В программе это делается путем выполнения в цикле строки
t[i]=topt[i]+(tpess[i]-topt[i])*bet23();
2. Обращаемся к программе cripa и находим длину критического пути
l=cripa(nv,nrab,begin,end,t); (1)
В теории имитационного моделирования получение одного згачения интересующей нас величины называют прогоном модели. Далее надо задаться каким-либо значением числа прогонов n и повторить пункты 1 и 2 n раз.
Полученную выборку из n значений критического пути далее надо подвергнуть статистической обработке. Однако, выгоднее совместить эту обработку с циклом прогонов. Для поставленных в задании задач обработки это делается так.
Построение гистограммы.
В работе 7 получены длины критических путей для оптимистических и пессимистических оценок продолжительностей работ. Обозначим их lopt иlpess
Очевидно наша случайная величина будет меняться на отрезке [lopt,lpess]
Для определения в какой разряд гистограммы попадает вычисленное в (1) значение l
добавим в главный цикл после строчки (1) такие
j=(l-lopt)/(lpess-lopt)*nr;
gist[j]++; (2)
(См. Лабораторную работу 5). После выхода из цикла прогонов можно прямо обращаться к программе построения гистограммы.
Оценка математического ожидания и дисперсии
Если ![]() значения
длины критического пути, вычисляемые в цикле прогонов, то наилучшей оценкой математического ожидания
является выборочное среднее
значения
длины критического пути, вычисляемые в цикле прогонов, то наилучшей оценкой математического ожидания
является выборочное среднее
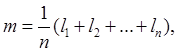 (3)
(3)
а оценкой дисперсии величина
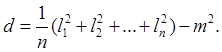 (4)
(4)
оценкой Стоящие в скобках суммы также выгодно накапливать в главном цикле. Для этого вводятся переменные s1 и s2. Перед главным циклом они обнуляются а в главный цикл после строки (2) добавляем
s1=s1+l; s2=s2+l*l;
ваПосле выхода из цикла прогонов по формулами (3) и (4) получаем нужные оценки.
Задание.
1) Многократно генерируя продолжительности работ в соответствии с их распределением, построить гистограмму ,получить оценки математического ожидания и дисперсии длины критического пути.
2) Считая закон распределения длины критического пути нормальным, найти доверительный интервал, в который длина критического пути попадает с вероятностью 0,9.
3) Сравнить полученные результаты с длинами критических путей из работы 7.
Оформление отчета.
Отчет должен содержать:
- текст программы для выполнения задания и результаты ее работы..
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.