Программа для расчета и оптимизации сетевого графика. Сопроводительная документация. Описание алгоритма функционирования программы, страница 5

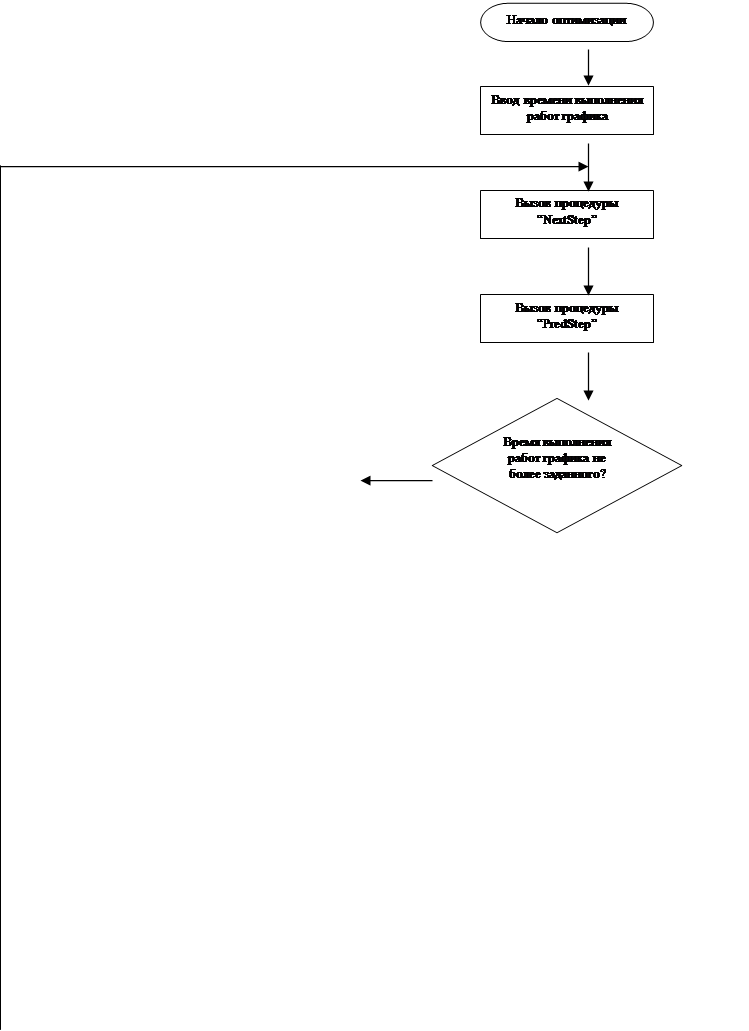
В основу оптимизации сетевого графика положен следующий метод. Сетевой график сначала расчитывается путем последовательного вызова процедур “NextStep” и “PredStep”, а затем по результатам расчетов определяется, соответствует ли время выполнения работ графика требуемому, а минимальный коэффициент напряженности заданному значению.

В случае, если время выполнения работ сетевого графика превышает требуемое, то на всех работах, где ключ возможности коррекции количества людей установлен, количество задействованных людей удваивается, при этом время выполнения работ графика уменьшается. На этом завершается итерационный цикл, после чего он начинается заново.

Если коэффициент напряженности минимального пути ниже требуемого, то берется кратчайший путь и по его работам распределяются люди таким образом, чтобы разница между временем выполнения работ с возможностью изменения количества людей и временем критического пути распределялась прямо пропорционально полному резерву работы.

 

Удвоение количества людей на работах

нет

 

                                                          да

 

да

Увеличение максимального времени выполнения работ графика

                                                     нет

	Коррекция количества людей на работах короткого пути, доступных для коррекции

 

нет

 

да                                           да

Сообщение об ошибке оптимизации

Рисунок 3.3 – Блок-схема алгоритма оптимизации.

Если коэффициент напряженности минимального пути соответствует требуемому, а время выполнения работ графика ниже требуемого с некоторой точностью (е=97%), то есть меньше нижней границы, то время критического пути увеличивается на 1/5 разницы между заданным и критическим временами. Это сделано, исходя из точки зрения, что приближение к требуемой точке может быть произведено только с одной стороны путем увеличения времени выполнения работ на незначительную величину. Малое значение приращения объясняется тем, что при оптимизации критические пути могу меняться              (т.е. увеличиваться), что может привести к превышению требуемого времени выполнения работ графика в случае большого значения приращения, а процесс приближения – оказаться колебательным. Коэффициент пропорциональности подобран экспериментально.

В случае, если при оптимизации программа зацикливается на одном минимальном пути, то эта ситуация распознается, и выдается соответствующее сообщение о том, что данный график оптимизировать нельзя.

3.5 Вывод результатов.

При выводе результатов происходит вывод всех либо критических путей в зависимости от установленного режима, характерик графика – время выполнения работ графика и минимальный коэффициент напряженности, перечень событий в порядке возрастания порядковых номеров и перечень работ в порякде возрастания номеров начальных событий работ графика. Все это реализуется в виде простейших циклов.

ЗАКЛЮЧЕНИЕ

В данном документе была изложена краткая теория по построению сетевых графиков, расчету их параметров и оптимизации.Для реализации указанных задач на ЭВМ была предложена программа NetGraph на языке Turbo_Pascal 7.0, изложены алгоритмы ee функционирования и инструкция пользования программой.

Остается надеятся, что разработанная программа найдет широкое применение в сетевом планировании.