Дирекционные углы линий. Прямая геодезическая задача. Составление топографического плана участка местности

Задача 1. Вычислить дирекционные углы линий ВС и CD, если известны дирекционный угол α_АВ линии АВ и измеренные правые по ходу лежащие углы β₁ и β₂ (рис. 1).

Исходный дирекционный угол α_АВ берется в соответствии с шифром и фамилией студента: 48°38,2’

Правые углы при точках В и С равны: β₁ = 189°59,2'; β₂ = 168°50,8'.

α _ВС= α_АВ  + 180° –  β₁=48°38,2’+ 180°-189°59,2'=38°39.0';

α_CD = α_ВС+ 180° – β₂=38°39.0'+ 180°-168°50,8'=49°48.2'

Задача 2.  Решить прямую геодезическую задачу, т.е. найти координаты х_С и у_С точки С (рис. 1), если известны координаты х_В и у_B точки В, длина (горизонтальное проложение) d_BС линии ВС и дирекционный угол α_ВС  этой линии.

Координаты точки В и длина d_ВС берутся одинаковыми для всех вариантов: х_В = – 14,02 м,  y_B = +627,98 м,  d_ВС  = 239,14 м.

Дирекционный угол α_ВС линии ВС следует взять из решения предыдущей задачи.

Координаты точки С  вычисляются по формулам:

x_С= х_В + Δx_BC=-14,02+186,76=+172,74 м;

y_С = y_В + Δy_ВС=+627,98+149,36=+777,34 м, где Δх_ВС и Δу_ВС — приращения координат, вычисляемые из соотношений:

Δх_ВС = d_ВС cos α_ВС=239,14∙cos 38°39.0'=+186.76 м ;

Δу_ВС = d_ВС sin α_ВС=239,14∙sin 38°39.0'=+149.36 м.

Составление топографического плана  участка местности

По данным полевых измерений составить и вычертить топографический план участка в масштабе 1: 2000 с высотой сечения рельефа 1 м. Решить отдельные задачи.

Работа состоит из следующих этапов: обработка ведомости вычисле-ния координат вершин теодолитного хода; обработка тахеометрического журнала; построение топографического плана; решение задач по топографическому плану.

Исходные данные и задания

1. Для съемки участка на местности был проложен замкнутый высотно-теодолитный ход I, II, III, IV и V  с привязкой к пунктам  ПТ 15 и ПТ 16 Государственной геодезической сети (рис. 2). В нем были измерены  длины  всех сторон, а также на каждой вершине хода — правый по ходу горизонтальный угол и углы наклона на предыдущую и последующую вершины.

Измерение углов производилось теодолитом 2Т30.

Результаты полевых измерений по теодолитному ходу горизонталь-ных углов β, углов наклона ν и линий S занесены в табл. 1, а по тахеометрическому ходу занесены в табл. 5. Как одни, так и другие результаты  являются общими для всех вариантов.

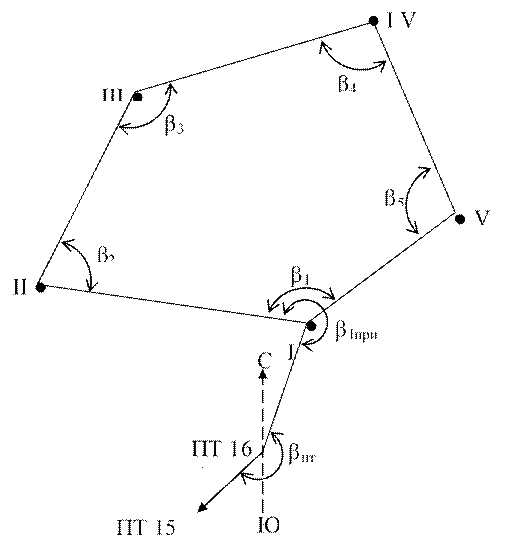
Рис. 2. Схема высотно–теодолитного хода съемочного обоснования

Таблица 1

Результаты полевых измерений по высотно-теодолитному ходу

№№ точек	Измеренные углы		Длина сторон, S, м	Горизонтальные проложения, d, м
	горизонтальные, β	вертикальные, v
ПТ 15
ПТ 16	1620 23,5/
		20 05/	305.92	305,72
I	3090 59,2/
		00 54/	263.05	263.02
II	500 58,5/
		00 06/	238,51	238,51
III	1610 20,0/
		00 12/	269.80	269.80
IV	790 02,8/
		20 06/	190.21	190.08
V	1080 17.5/
		00 49/	239,16	239.14
I	140020,2/
II

Известны координаты пунктов триангуляции ГГС ПТ 15 и ПТ 16, которые выбираются из табл.2 по последней цифре шифра и количества букв в фамилии студента:  координаты Х и У опорных пунктов равны величинам таблицы в строке, соответствующей последней цифре шифра, за исключением координаты Х ПТ15, значение которой увеличивается  на величину произведения количества букв в фамилии студента  на 100.

Таблица 2

Координаты опорных точек ПТ15 и ПТ16

Последняя цифра шифра	Координаты ПТ 15		Координаты ПТ 16
	Х15	У15	Х16	У16
8	1350,70	1490,60	755,00	980,50

3. Отметка пункта ПТ 16 обычно известна из геометрического нивелирования. При выполнении же задания значение отметки ПТ 16 следует принять условно: количество целых метров в отметке должно быть трехзначным числом, в котором количество сотен метров равно единице, а количество десятков и единиц метров составляют две последние цифры шифра студента. В дробной части отметки (дм, см, мм) повторяются  цифры, что и в целой части.

Н₁₆=  148,148 м

Вычисление координат съемочного обоснования

Увязка углов хода. Значения измеренных углов и величины горизонтальных проложений записывают в графу 2 и 7 ведомости вычисления координат (табл. 3). Вычисляют сумму Σβ_пр. измеренных углов замкнутого хода (полигона). Определяют теоретическую сумму углов  Σβ_т = 180⁰(n – 2), где n — число вершин хода.

Примечание. При нахождении суммы Σβ_пр. используются только внутренние углы пятиугольника. Углы висячего хода на точках ПТ16 и     ст. I (βПТ  и β1прим ) в данной задаче не увязываются.

Отсюда угловая невязка будет равна:  f_β = Σβ_пр. - Σβ_т. = Σβ_пр. – 540⁰

Если невязка f_βне превышает допустимой величины доп. f_β = ±1', то ее распределяют с обратным знаком поровну на все углы хода, то есть δ_β =  –   с округлением значений поправок до десятых долей минут. Исправленные указанными поправками углы записывают в графу 3 ведомости. Сумма исправленных углов должна равняться теоретической.

После этого приступают к вычислению дирекционных углов и румбов сторон хода. Для этого необходимо знать исходный дирекционный угол α₀, для чего решается обратная геодезическая задача.

В нашем примере (см. табл. 2) даны координаты Х и У пунктов триангуляции ПТ 15 и ПТ 16, разность которых равна: = - 595,70   и

= -510,10.  Тогда  румб  опорной линии ПТ 15 – ПТ 16   будет  равен: r_15-16  = arctg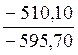 = 40⁰ 34,4^/  в юго-западной четверти.

Отсюда искомый дирекционный угол линии 15 – 16  будет равен:

α_15-16 = 180⁰ + 40⁰34,4^/ = 220⁰ 34,4^/. Этот угол и будет исходным для вычисления дирекционных углов всех сторон теодолитного хода. Для этого величину дирекционного угла и румба записываем в графы