лентной схемы двухполюсника переменного тока может быть реРазделы курса, охватываемые работой:шена различными методами, основные из которых описываются — анализ цепей гармонического тока в установившемся режи-ниже.
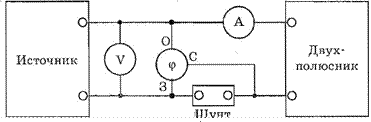
ме;1.1. С помощью вольтметра, амперметра и фазометра по схеме
— эквивалентные параметры пассивного двухполюсника и ме-(рис. 1) измеряют входное напряжение U , ток и угол сдвига по тоды их экспериментального определения.
 Литература: [1, с. 184—189; 2, с. 84—85; З, с. 110—112; 4,
с. 51—
Литература: [1, с. 184—189; 2, с. 84—85; З, с. 110—112; 4,
с. 51—![]()
1, Методические указания
Объектом исследования является сложная цепь, заданная в виде пассивного двухполюсника и питаемая от источника гармонического напряжения.Рис. 1. Схема измерений с фазометром
2425
фазе между ними (Р. По измеренным величинам строят векторную диаграмму и, разложив вектор U на активную U а и реактивную Uр составляющие, вычисляют параметры последовательной эквивалентной схемы замещения по формулам
![]() Ucosp=acosp, хэ
Ucosp=acosp, хэ ![]() U Usinp =asinp. (2)
U Usinp =asinp. (2)
Построив снова по тем же данным векторную диаграмму и разложив вектор тока I на активную 1а и реактивную Ip составляющие, вычисляют параметры параллельной эквивалентной схемы замещения по формулам
![]() ICOS(f) = Уэсоыр, Вэ =
ICOS(f) = Уэсоыр, Вэ =![]()
1.2. С помощью вольтметра, амперметра и ваттметра по схеме (рис. 2) измеряют входное напряжение U , ток I и активную мощность Р. По данным измерений вычисляют параметры эквивалентных схем по формулам
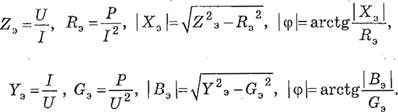 (4)
(4)
Приведенные формулы позволяют определить знак угла ф, знак реактивного сопротивления Хэ и реактивной проводимости вэ.
Для экспериментального определения характера исследуемого двухполюсника последовательно с ним включают добавочное
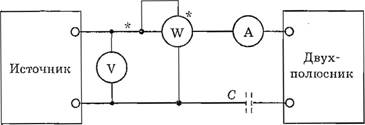
Рис. 2. Схема измерений с ваттметром
 26
26
реактивное сопротивление хд, знак которого известен заранее, измерения повторяются при неизменной величине приложенного напряжения. Если при этом ток и мощность, потребляемые цепью, уменьшаются, следовательно, результирующее реактивное сопротивление цепи возрастает, а это значит, что знаки Хд и Хэ одинаковы, В случае увеличения тока и мощности Х и хэ имеют разные знаки, так как результирующее реактивное сопротивление снижается. Все это справедливо, если хд подобрано так, что выполняется условие
![]()
Задачу по определению характера цепи можно также решить включением параллельно двухполюснику добавочной реактивной проводимости известного знака. В этом случае увеличение тока и мощности указывает на совпадение характера добавочной проводимости и двухполюсника.
1.3 Определение параметров эквивалентных схем методом «трех вольтметров» .
В этом случае собирается схема (рис. З, а), где Ред — добавочный резистор, величина активного сопротивления которого заранее известна.
С помощью вольтметра измеряются напряжения U 1, (.Јд и U. По известным величинам напряжений, как по трем сторонам треугольника, строится векторная диаграмма (рис. З, б). После этого вектор напряжения U раскладывается на активную Uа и реактивную Up составляющие, как это показано на рис. З, б (векторная диаграмма построена для случая (Р < О).
а)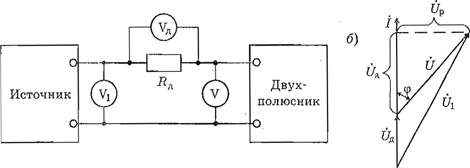
Рис. З. Определение параметров эквивалентных схем по метоДу
«трех вольтметров»: а — схема измерений; б — векторная Диаграмма
27
Зная величину Рьд, можно найти ток по формуле закона Ома![]()
![]() д (5)
д (5)
а затем по формулам (2) вычислить эквивалентные параметры последовательной схемы. Параметры параллельной схемы можно вычислить по формулам перехода (1).
1.4. Определение параметров эквивалентных схем методом
«трех амперметров» .
В этом случае собирается схема (рис. 4, а), где
добавочный резистор Вд включен параллельно двухполюснику и его сопро- ![]() тивление
известно заранее. С помощью амперметра измеряются величины токов 11, 1д и 1. По
этим данным строится векторная диаграмма токов и ток I раскладывается на активную
Га и реактивную 1 р составляющие. Пример такой диаграммы для случая (Р 0
приведен на рис. 4, б. Зная величину вд, можно определить величину приложенного
напряжения
тивление
известно заранее. С помощью амперметра измеряются величины токов 11, 1д и 1. По
этим данным строится векторная диаграмма токов и ток I раскладывается на активную
Га и реактивную 1 р составляющие. Пример такой диаграммы для случая (Р 0
приведен на рис. 4, б. Зная величину вд, можно определить величину приложенного
напряжения
![]()
По формулам (З) вычисляются параметры эквивалентной параллельной схемы, а по формулам перехода (1) — параметры последовательной схемы,
Следует отметить, что в опытах 1.3 и 1.4 внак угла (Р и реактивного сопротивления Хэ остается неопределенным. Для определения этого знака нужно провести дополнительный опыт, как в п. 1.2.
|
Источник |
|
Двухполюсник |
а) б)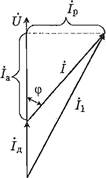
![]()
Рис. 4. Определение параметров эквивалентных схем по метоДџ «трех амперметров»: а — схема измерений; б — векторная Диаграмма
![]()
 28
28
2. Подготовка к работе
2.1. Изучить методические указания к работе и литературу.
2.2. Из таблицы вариантов (табл. 1) для своего номера выбрать величины U, 1, Р, характер двухполюсника.
Таблица 1
U = 25 в Варианты задания
|
Параметр |
двухполюсника |
Вариант |
|||||||||
|
1 |
2 |
з |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
I, мА |
180 |
184 |
170 |
181 |
180 |
170 |
160 |
178 |
170 |
163 |
|
|
п |
142 |
151 |
88 |
74 |
143 |
121 |
66 |
82 |
82 |
82 |
|
|
Р, вт |
2,4 |
2,5 |
2,4 |
2,43 |
2,1 |
1,88 |
2,25 |
1,95 |
|||
|
2,1 |
2,25 |
0,75 |
2,1 |
1,5 |
0,6 |
0,68 |
0,98 |
0,75 |
|||
2.3. Рассчитать параметры эквивалентных схем двухполюсник“
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.